BC-Clarke and five-pointed star（水）

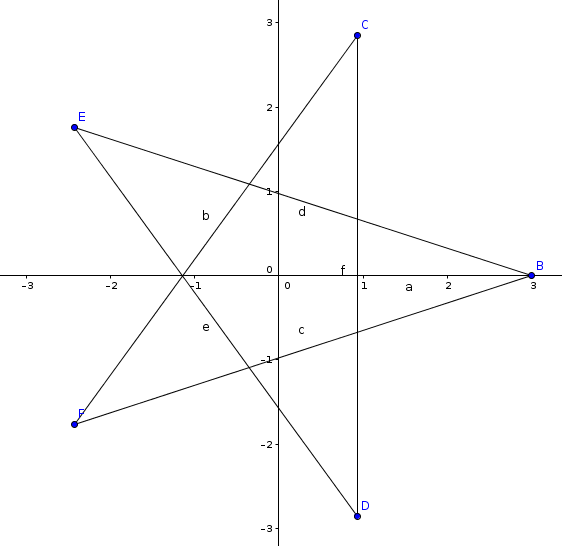
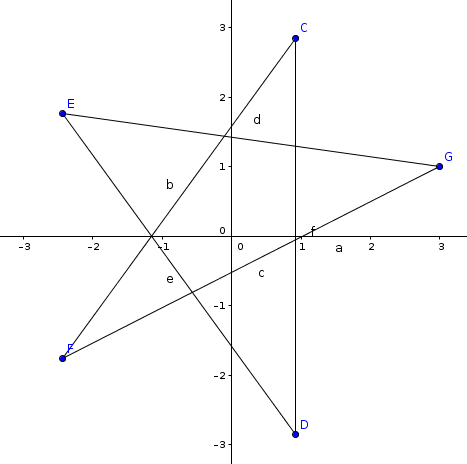
Clarke and five-pointed star

Accepts: 237

Submissions: 591

Time Limit: 2000/1000 MS (Java/Others)

Memory Limit: 65536/65536 K (Java/Others)

Problem Description

Clarke is a patient with multiple personality disorder. One day, Clarke turned into a learner of geometric.
When he did a research with polygons, he found he has to judge if the polygon is a five-pointed star at many times. There are 5 points on a plane, he wants to know if a five-pointed star existed with 5 points given.

Input

The first line contains an integer $T(1\le T\le 10)$, the number of the test cases.
For each test case, 5 lines follow. Each line contains 2 real numbers xi,yi(−109≤xi,yi≤109)x_i, y_i(-10^9 \le x_i, y_i \le 10^9)x​i​​,y​i​​(−10​9​​≤x​i​​,y​i​​≤10​9​​), denoting the coordinate of this point.

Output

Two numbers are equal if and only if the difference between them is less than 10−410^{-4}10​−4​​.
For each test case, print $Yes$ if they can compose a five-pointed star. Otherwise, print $No$. (If 5 points are the same, print $Yes$. )

Sample Input

2
3.0000000 0.0000000
0.9270509 2.8531695
0.9270509 -2.8531695
-2.4270509 1.7633557
-2.4270509 -1.7633557
3.0000000 1.0000000
0.9270509 2.8531695
0.9270509 -2.8531695
-2.4270509 1.7633557
-2.4270509 -1.7633557

Sample Output

Yes
No

简单的判断是不是正五边形，就过。。。

官解：

容易看出只需要判断这5个点是否在一个正五边形上。

因此我们枚举排列，然后依次判断即可。

判定方法是，五条相邻边相等，五条对角线相等。

当然题目给的精度问题，窝只能说，如果泥做法不复杂，精度足够好的话，是可以过的。毕竟题目说的小于10−410^{-4}10​−4​​是指理论上的，所以理论上适用所有的数之间的比较。所以有人问我开方前和开方后，我只能说，哪个精度高用哪个....

当然你也可以先求出凸包然后再判相邻距离......

#include <iostream>
#include <string.h>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#include <stdio.h>
using namespace std;

double  x[10],y[10] ;
int main()
{
    int T;
    scanf("%d",&T);
    double dis[10][10];
    while(T--)
    {
        for(int i = 0 ; i < 5 ; i++){
          scanf("%lf%lf",&x[i],&y[i]);
        }
        bool is = true;
       // printf("---------------");
        for(int i=0;i<5;i++){
            for(int j=0;j<5;j++){
                if(i==j)
                    continue;
                else{
                  dis[i][j] = (x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]);
                 // printf("%lf ",dis[i][j]);
                }
            }
            //printf("\n");
        }
        double mmax=dis[0][1],mmin = dis[0][1];
        for(int i=2;i<5;i++){
            if(mmax<dis[0][i]) mmax = dis[0][i];
            if(mmin>dis[0][i]) mmin = dis[0][i];
        }
        for(int i=0;i<5;i++)  ///其他距离
            for(int j=0;j<5;j++){
              if(i==j) continue;
              if( fabs(dis[i][j]-mmin)>0.0001 && fabs(dis[i][j]-mmax)>0.00001)
                is = false;
            }
        if(!is){
            printf("No\n");
            continue;
        }
        int adj[] = {-1,-1,-1,-1,-1};  ///相邻边距离
        int coun = 0;
        int i=0;
        while(1){
            if(coun == 5) break;
            for(int j=0;j<5 && adj[i]==-1;j++){
                if(i==j) continue;
                if( fabs(dis[i][j]-mmin)<0.0001 ){
                    int k;
                    for(k=0;k<5;k++)
                        if(j==adj[k]) break;
                    if(k==5)
                       adj[i] = j,i=j,coun++;
                }
            }
        }
        for(i=0;i<5;i++)
            if(adj[i]==-1)
             is = false;
        if(!is){
            printf("No\n");
            continue;
        }
        for(i=0;i<5;i++){  ///对角线距离
            int adj1=adj[i],adj2;
            for(int j=0;j<5;j++){
                if(adj[j] == i){
                    adj2=j; break;
                }
            }
            for(int j=0;j<5;j++){
                if(j!=adj1&&j!=adj2&&j!=i){
                    if(fabs(dis[i][j]-mmax)>0.0001)
                        is = false;
                }
            }
        }
        if(!is){
            printf("No\n");
            continue;
        }
        printf("Yes\n");
    }
    return 0;
}