机器学习（一）
一、机器学习介绍
什么是机器学习？计算机程序从经验E（给一些样本数据）中学习任务T，用度量P来衡量性能，并且由P定义的关于T的性能会随着经验E而提高
机器学习分为：有监督学习（给出数据样本的标签）、无监督学习（没有给出数据样本的标签）、半监督学习（给出少量的有标签数据，和大量没有标签的数据）、强化学习（对输入的数据做出评价）
机器学习的过程如下所示：
即由训练数据，输入学习算法，得到模型的假设函数，例如，由房屋尺寸和价格得到的房屋价格预测模型，由输入房屋尺寸，经过模型h，得到估计的房屋价格
为什么机器学习由训练的数据样本训练出的模型，在另外的测试样本中经过这个模型可以得到近似真实的结果？
以从瓶中抽取弹珠为例：
假设，总的样本中橘色弹珠的比例为
，随机抽取出的样本中橘色弹珠的比例为
，这两个比例值相差的概率符合公式：
，由公式可以看出，两个比例值相减的差值大于某一值
，由于后面的
随着
的增大而减小，公式说明两个比例值相差很大的概率是很小的，说明在一定程度上抽取的样本训练模型可以代表真实的模型，但只是大致相近，不能等同与真实模型，那么怎么保证由样本训练出的模型无限接近于真实的模型？
引入三个符号，训练时的误差Ein和测试模型的误差Eout，以及代表模型复杂度的
，训练模型时要Ein尽可能的小（理想情况下为0），无限接近真实的模型同样要Eout尽可能的最小，模型的假设函数用g表示，则对于一个模型函数g的Ein和Eout的关系表示为
，
当模型复杂度很高时，模型的假设函数的集合就会很大，在众多集合中搜寻到一个使训练样本的Ein很小的假设函数g是可能的，即当模型的复杂度很高时，训练样本的Ein会很容易变得很小，但由公式可以看出，当模型复杂度很高时，测试样本的误差Eout是有可能很高的，即使得模型的泛化能力很低，只有在训练样本数量N足够大时，才能使更复杂（即参数更多或者说VC维更大）的模型出现Eout很大情况的几率变小，dvc、N、Ein、Eout、模型复杂度的关系可表示为
所以较高的模型复杂度会很容易造成过拟合，为了避免过拟合的发生，其中一个方法是收集大量的数据，理论上数据样本N和模型复杂度dvc的关系为
，但实际上需要
就足够了，另外尝试机器学习要从简单的模型（例如从简单的线性模型）做起，如果得到的Ein很小，再测试Eout，如果能够得到很好的效果不需要复杂模型，若得到的Ein很高再考虑复杂的模型。
二、线性回归 linear regression
线性回归模型，由一系列输入得到一个实数的输出
一个输入特征为2维的线性回归，
，假设函数中的
参数称为权重，目的是求得这个函数的合适的权重
那么什么是合适的参数？合适的就是要使所有样本输入的特征与其对应相乘得到的
和样本给出的标签y的值尽可能的接近，即y和
的差要最小
由此可得代价函数
，其中m为训练的样本数，用平方错误来衡量代价，我们的目标就是使
最小，即
对于同一批训练样本来说，不同的参数计算出来的最终代价函数值是不同的，假设下图所示不同的与的分布图
对于一个函数来说，最小值的点在最低点，即函数的梯度为零的点，刚开始的梯度不为0，使梯度逐步下降直到最优解或局部最优解出现
算法可表示为
其中，
代表每个特征对应的参数，
为步长，更新参数时要同时更新，不能完全更新完其中一个权重，然后再更新另一个权重，正确的方法（左）和错误的方法（右）分别为为
错误的原因是在同一次的迭代中，计算
使用了更新后的
的值
为什么使用
这种形式可以达到目标？以一个参数的代价函数为例，一个参数的代价函数是一个二次的抛物曲线（凸函数），如下图所示
代价函数最小的点的参数在最低点，当在最低点的右边时，由对代价函数对进行求导可得一个正数的斜率，为正与正斜率的乘积是一个正数，减去一个正数会慢慢减小直至最低点
当在最低点的左边时，由对代价函数对进行求导可得一个负数的斜率，为正与正斜率的乘积是一个负数，减去一个负数会慢慢增大直至最低点，这是特征一维的情况，可以推广到多维
所以，对于梯度下降的方法可以得到最优解或者局部最优解，对于的取值，如果取值太小，则速度会很慢，若取值太大则较大步长可能会无法收敛；取得一个合适的值，
会随着迭代的次数逐渐变小，所以梯度下降的幅度会逐渐减小，慢慢的接近最低点，不需要变更减小的值
把对代价函数代入可得
推广到多维特征的形式，假设函数为
，定义
，则假设函数变为一般形式为
（（n+1）*1应该为1*（n+1））
则梯度下降推广到多维的形式，可表示为
其中，
和
中的上标
代表的一个特征向量（即每一条数据），中的下标数字代表的是所要更新参数及其对应的特征向量的维度（即参数所在的那一维特征）
通常，对于特征向量，若各个维度的取值范围比较接近则梯度下降的速度会较快，若取值范围不同则下降会较慢，以二维的特征向量为例：
特征x1和x2的范围不同，梯度下降会很慢找到最优解 特征x1和x2 转化到相同的范围，梯度下降相对容易找到最优解
所以我们的目标是把特征约束在[-1,+1]这个范围内，超过这个范围很大或者在很小的范围内均不可取
可以利用特征缩放的方法，对特征向量的每一维进行处理，具体方法是（特征向量的维度-维度均值）/（维度最大值-维度最小值）或者（维度的标准差），例如
判断梯度下降是否工作，要看代价函数是否减小，其中一个方法是设定一个代价函数的阈值，例如
，当某一次迭代能够小于这个阈值则判定梯度下降正常工作，但这个阈值不容易设置，另一种方法是看迭代次数与代价函数值的关系曲线，看曲线值是否逐渐降低，例如
最小化代价函数值
能逐渐降低，并且在一定迭代次数之后，不再明显变化，说明梯度下降正常工作，且达到了最优或者局部最优
当出现例如上面三种情况，说明梯度下降不能正常工作，选取的步长的值太大，需要选取更小的值，通常的取值为
从小的值开始尝试，不同取值大约是3倍前值，当的取值较大时，梯度下降可能不能很好工作，再小的值也能使梯度下降缓慢到达最优或者局部最优，只是过小的值会使算法变慢，所以从小的值尝试，在梯度下降正常工作的情况下，尽可能选择一个较大的值。
三、多项式回归 polynomial regression
以预测房价为例，房子的长度作为特征x1，房子的临界宽带作为特征x2，房子的年龄作为特征x3，这时回归的模型为线性，若有新的恒量房子价格特征x为x1*x2或者x2*x3，这样的模型就不再是线性的，再比如我们收集的房子面积和价格的数据分布如下：
很显然，线性的模型不能很好的对数据进行拟合，需要非线性的曲线模型，这样就会使用特征的二次项、三次项或者其他方式来表达回归模型的项，这样的多项式回归是非线性模型，对于线性的模型来说，除了使用梯度下降方法以为，还可以使用标准方程法(Normal equation)，标准方程发的思想是对于一个凸函数，最优点是在最低点，即梯度为0的地方，求出代价函数对于参数的导数，令其等于0，所解出的参数值即为最优值，例如，对于一维度的情况
解出来的
值即为最优点的参数，推广到多维的情况，假设函数为
代价函数为，
解模型的推导过程如下：其中W和同等地位，m和N同等地位，代价函数的平方展开可以写为
，对参数W求导可得为2倍的
，令其等于0，可求得参数最终的解模型为
比如，一个四维特征的房价预测例子，
值得一提的是标准方程法不需要对特征进行归一化处理，不需要选择步长和迭代次数，但它的计算复杂度为
，特征维数较大时，计算很慢，另外
在大部分的情况下是可逆的，原因是在进行机器学习时，样本数量远远大于样本的特征维度，因此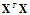
中存在足够的自由度使其可以满足可逆的条件，若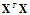不可逆，查看是否有重复特征维度或者太多的特征维度，删除一些特征或者使用正则化的方法。
这就是线性回归模型的标准方程的解法，对于非线性的模型来说，这种方法就不能使用了，能不能把非线性的多项式模型转化为线性模型？
对于非线性回归模型，例如
，可将每一个特征多项式变为一次项，即把X空间特征向Z空间转换，把非线性模型变为线性模型
数据样本从(x,y)变为
对于把Q次方的多项式进行全部的一次转换，转换的项数一共为
，转换过后的一次模型的dvc等于总的项数，选择合适的转换项数，项数越多代表模型越复杂，但不要为了减少dvc，人为的在脑袋里加工转换特征。
