[学习笔记] kd-tree
本文参考这位dalao的题解
前置技能:二叉查找树
其实kd-tree很简单的啦
和BST都差不多的啦
就是在划分的时候把每一维都比较一下就行啦
(\(dalao\)的kd-tree教程)
然而本蒟蒻是完全看不懂啊qwq
于是我们从头讲起吧:
step 1
首先,我们回忆一下BST,
它是以一个关键字\(val\),来满足它的两个性质反正大家都知道就懒得写了.
而kd-tree,则是对于一个\(k\)维的点(也就是有\(k\)个关键字),
来弄一个像BST的数据结构.
下面以2d-tree为例(也就是平面内的点)来介绍一下吧.
首先,看图:
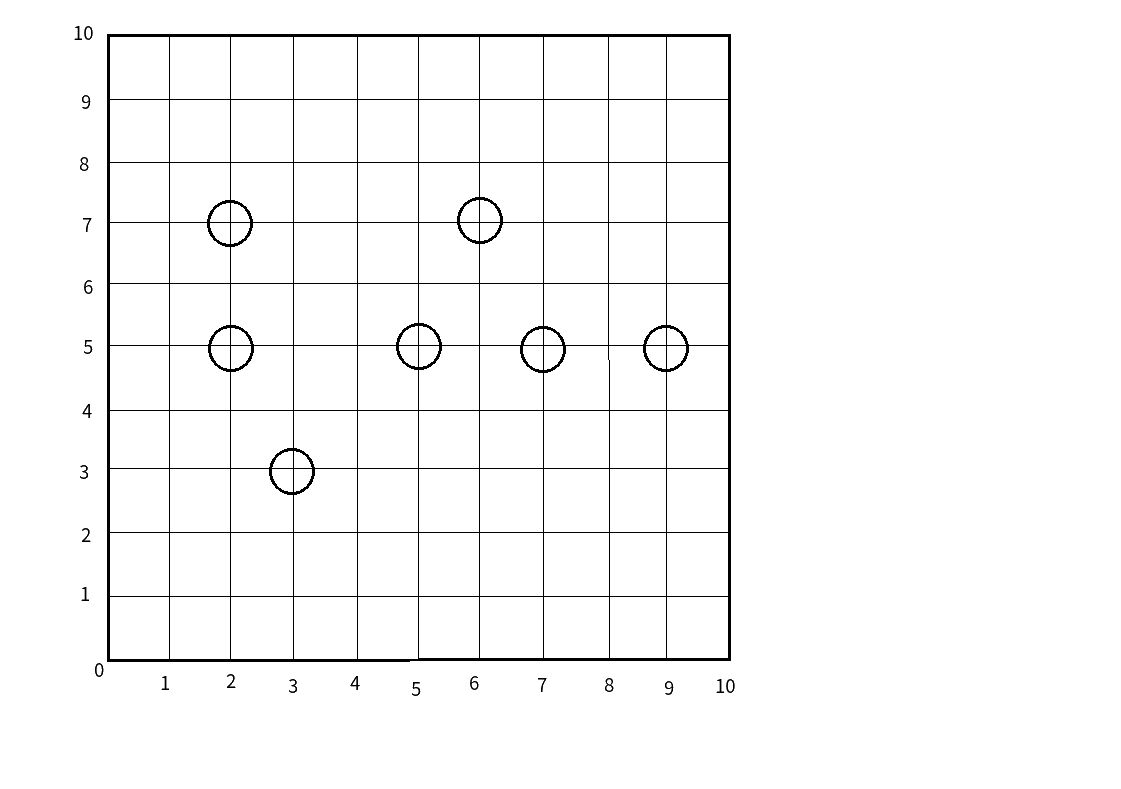
upd:图片出锅了.
(蒟蒻画图水平有限勉强看下吧)
如果我们只以一维来给这些点排序的话,(假设就以\(y\)轴)
我们会发现,\(x\)轴就没有了用处,
并且,中间的几个点还很尴尬(\(y\)轴都一样..)
因此,我们有一种划分的方法:
将每一维交替着划分.
比如说,我们这一层是以\(x\)轴划分的,
那么下一层就是以\(y\)轴划分.
这样建出来的树也很出色不要问我为什么人家也是蒟蒻qwq
step 2
接下来,就要正式讲建树了!
其实,划分的过程在上面已经讲了.
但是,为了保持树的平衡,
我们在建树的时候,可以直接取中间的点.
依然以上一张图为例吧,
首先,我们以\(x\)轴来划分,
那么中间的点显然就是这个红色的:

然后我们在将其它的点分成两部分:
.png)
(加粗的线即为分割线)
更加 直观一点的话,就是这样:
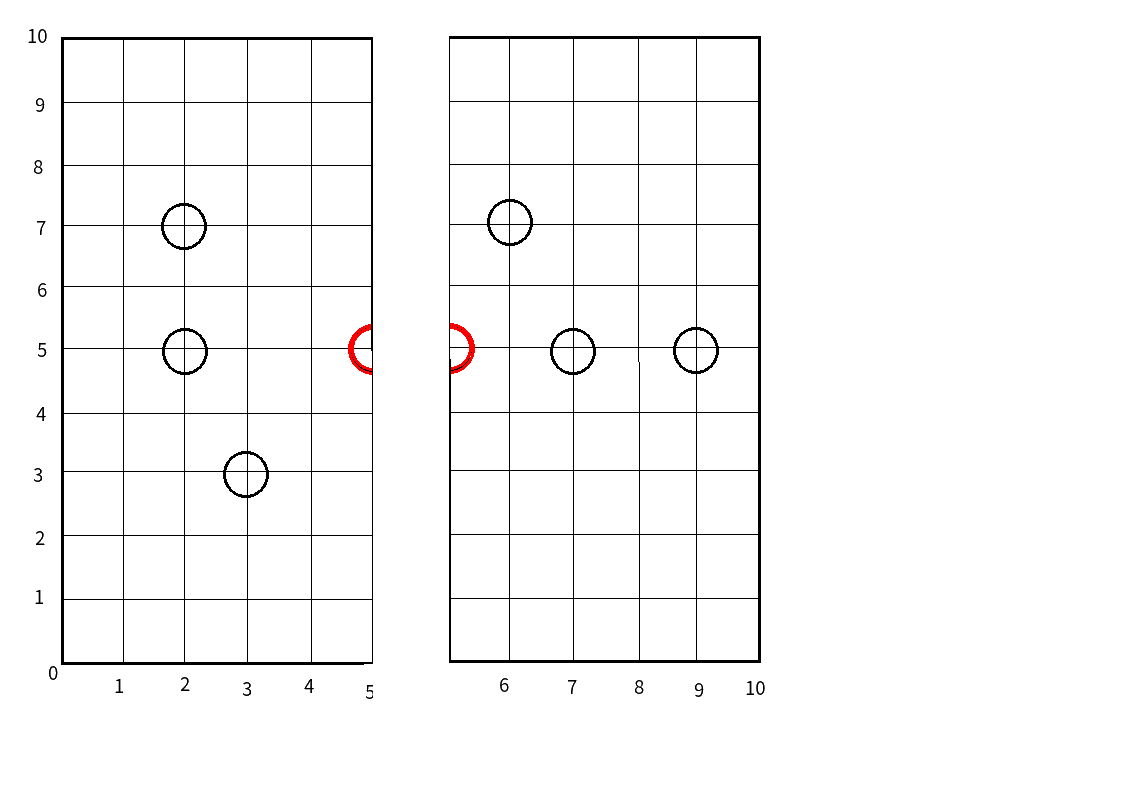
而我们建的树,就长这样(其实才就一个点):

接下来,我们再在它的两个儿子中以\(y\)轴来分,
由于有多个一样的点,我们随便找一个:

切开后就是这样:
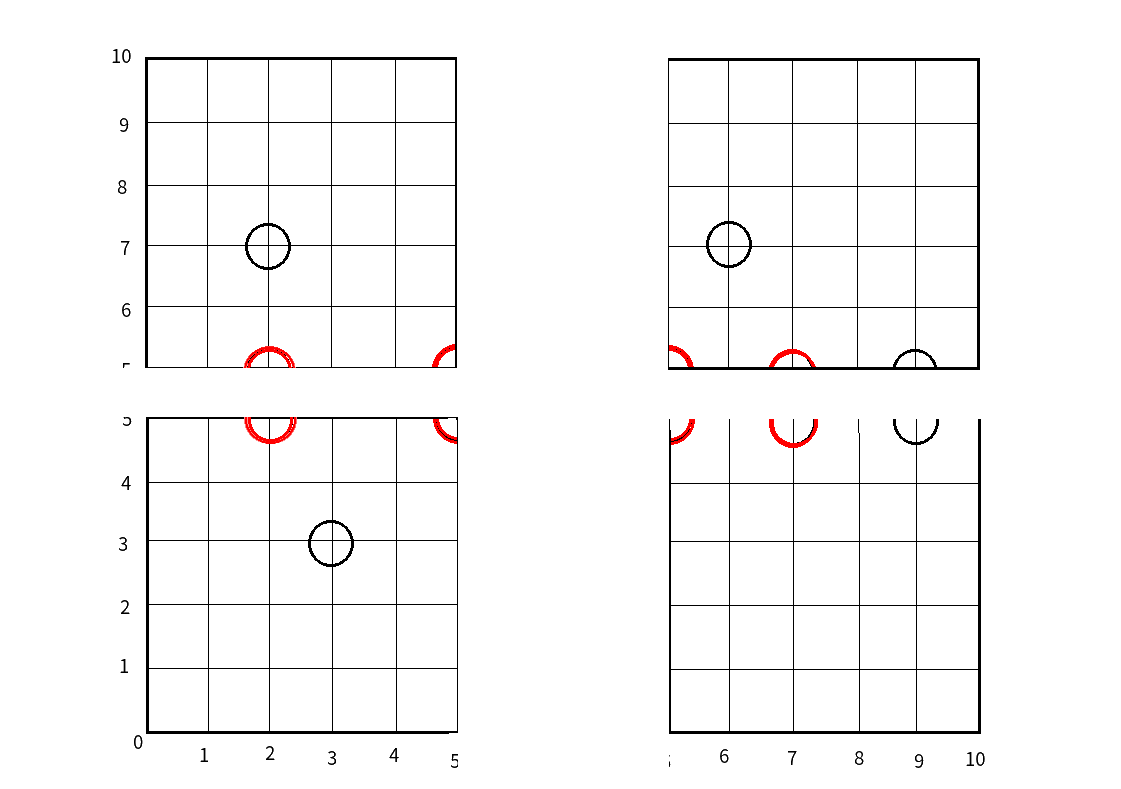
而树就长这样:

然后,我们再一个个分,最后就成了这样:
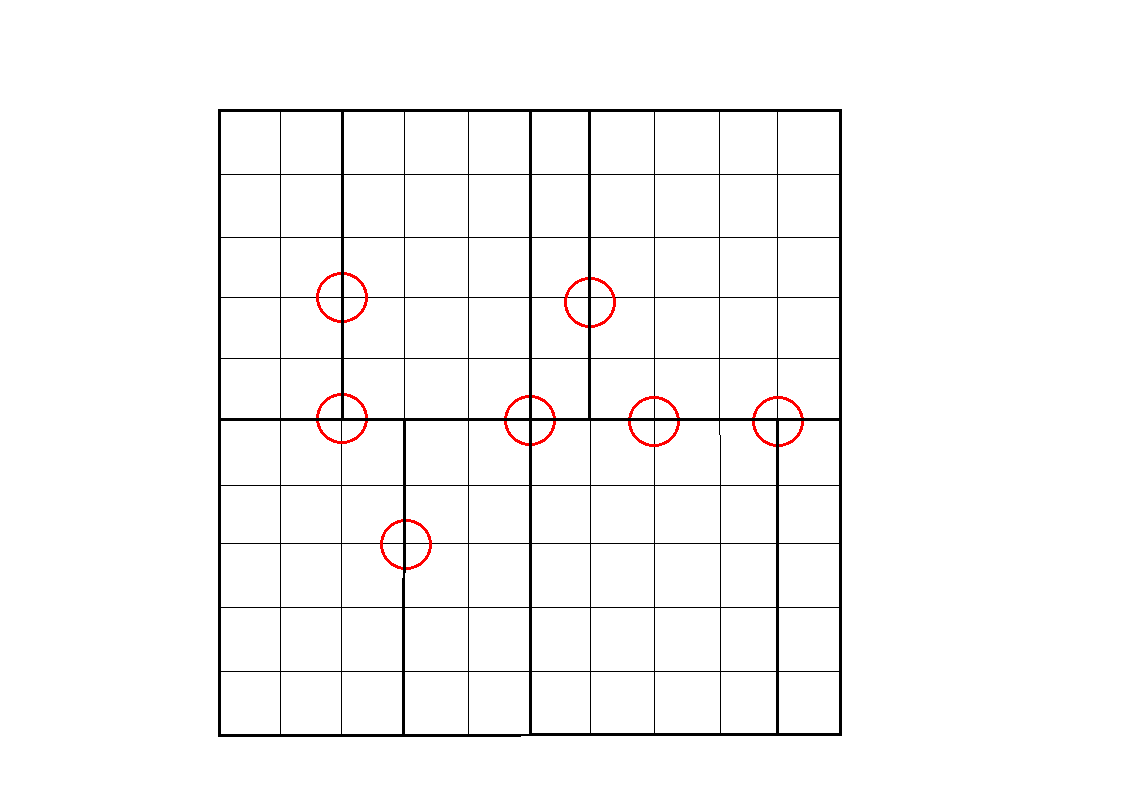
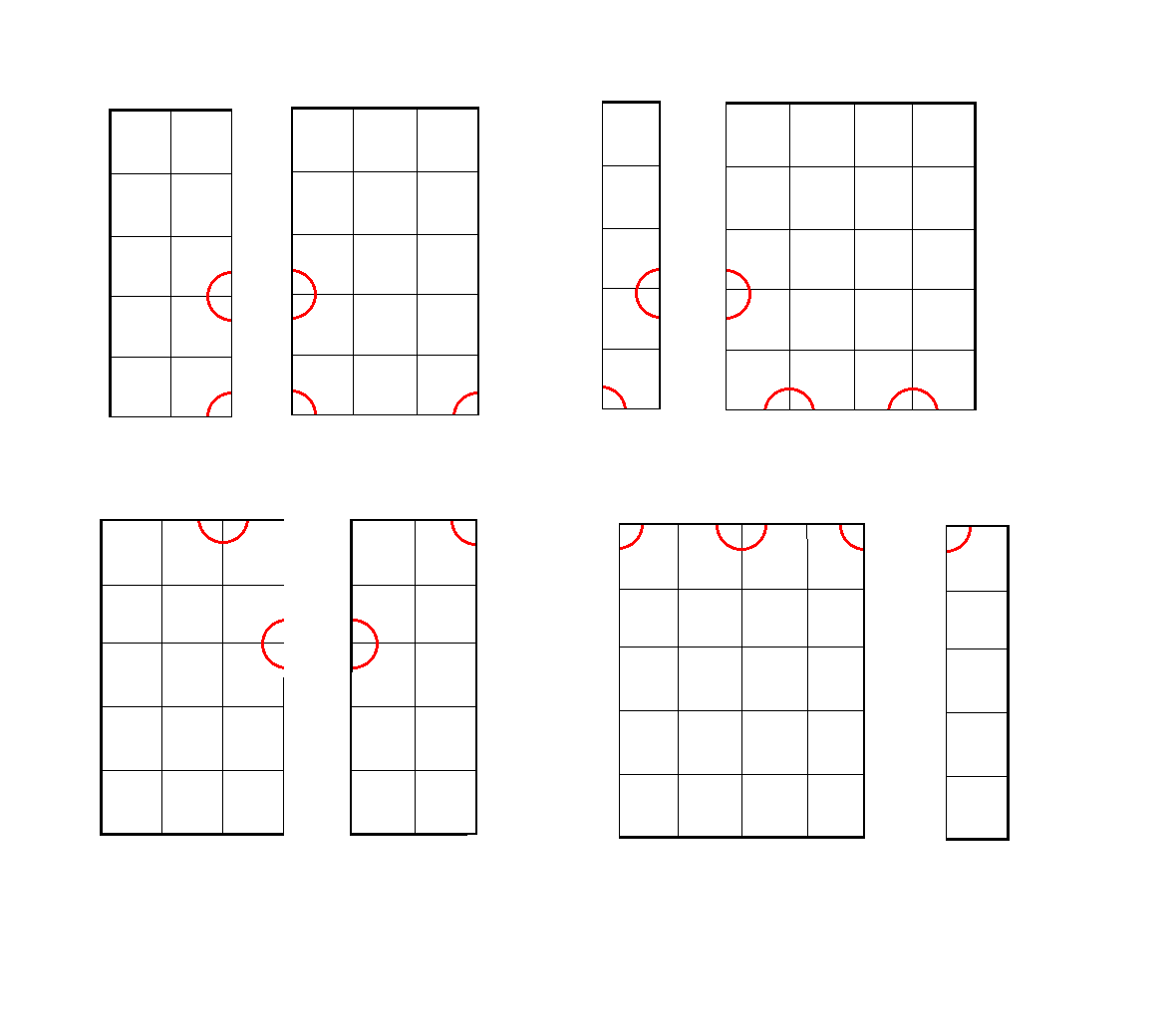
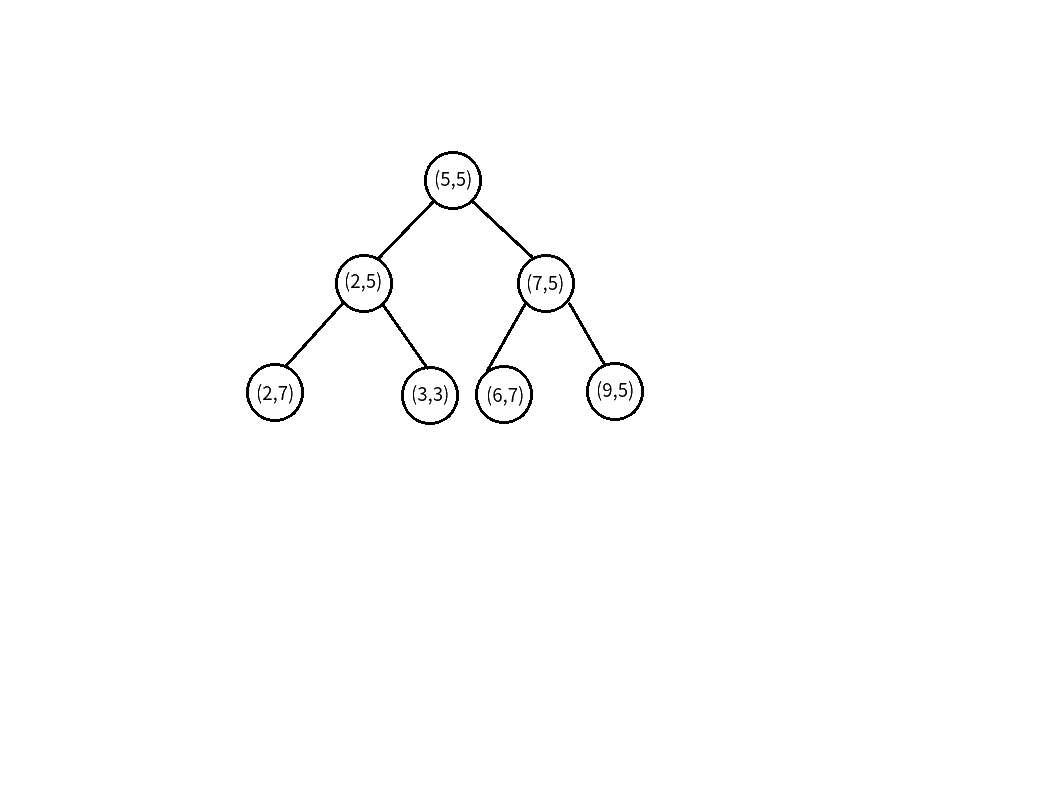
总之,就是说,在划分的时候,
我们先找到中间的那个点,将两边分割开来,
再对于两个儿子以另一维来分割.
并且,头文件algorithm还有一个方便的操作——函数:nth_element.
它能将序列中第\(k\)大的数放在第\(k\)位,
比\(k\)小的放在前面,比\(k\)大的放在后面(但是没有排序,也就是仅仅于第\(k\)大的比较).
代码如下:
nth_element(a+l,a+k,a+r+1,cmp);
所以说,建树的代码也可以出来了:
inline int New(){
if(top) return sta[top--];//这个地方先埋个坑(先不管它)
return ++tot;
}
bool cmp(node a,node b){return a.pla[now]<b.pla[now];}//now表示现在比较的是第几维
inline int build(int l,int r,int opt){
if(l>r) return 0;
int x=New(),mid=(l+r)>>1;now=opt;
nth_element(a+l,a+mid,a+r+1,cmp);t[x].place=a[mid];//这里表示当前的点的位置
t[x].ls=build(l,mid-1,opt^1);t[x].rs=build(mid+1,r,opt^1);
update(x);return x;//update等下会讲的
}
(感觉埋了好多坑了...)
step 3
接下来,让我们了解下每个节点储存的信息.(顺便说一句,本人沉迷于\(struct\))
\(ls,rs\):左儿子,右儿子.
\(size\):子树大小.
\(place\):一个结构体,表示点的位置.
\(mx[k]\):在当前节点的子树中第\(k\)维坐标最大值.
\(mi[k]\):在当前节点的子树中第\(k\)维坐标最小值.
其中,\(mx[k],mi[k]\)表示了当前节点及其子树的管辖范围(在查询时有用),
因此\(update\)就是来更新\(mx,mi,size\)的:
inline void update(int p){
for(int i=0;i<=1;i++){
t[p].mx[i]=t[p].mn[i]=t[p].place.pla[i];
if(t[p].ls) t[p].mx[i]=max(t[p].mx[i],t[t[p].ls].mx[i]),t[p].mn[i]=min(t[p].mn[i],t[t[p].ls].mn[i]);
if(t[p].rs) t[p].mx[i]=max(t[p].mx[i],t[t[p].rs].mx[i]),t[p].mn[i]=min(t[p].mn[i],t[t[p].rs].mn[i]);
}
t[p].size=t[t[p].ls].size+t[t[p].rs].size+1;
}
比如,我们拿之前的图,
红色的框就代表红色节点的范围:
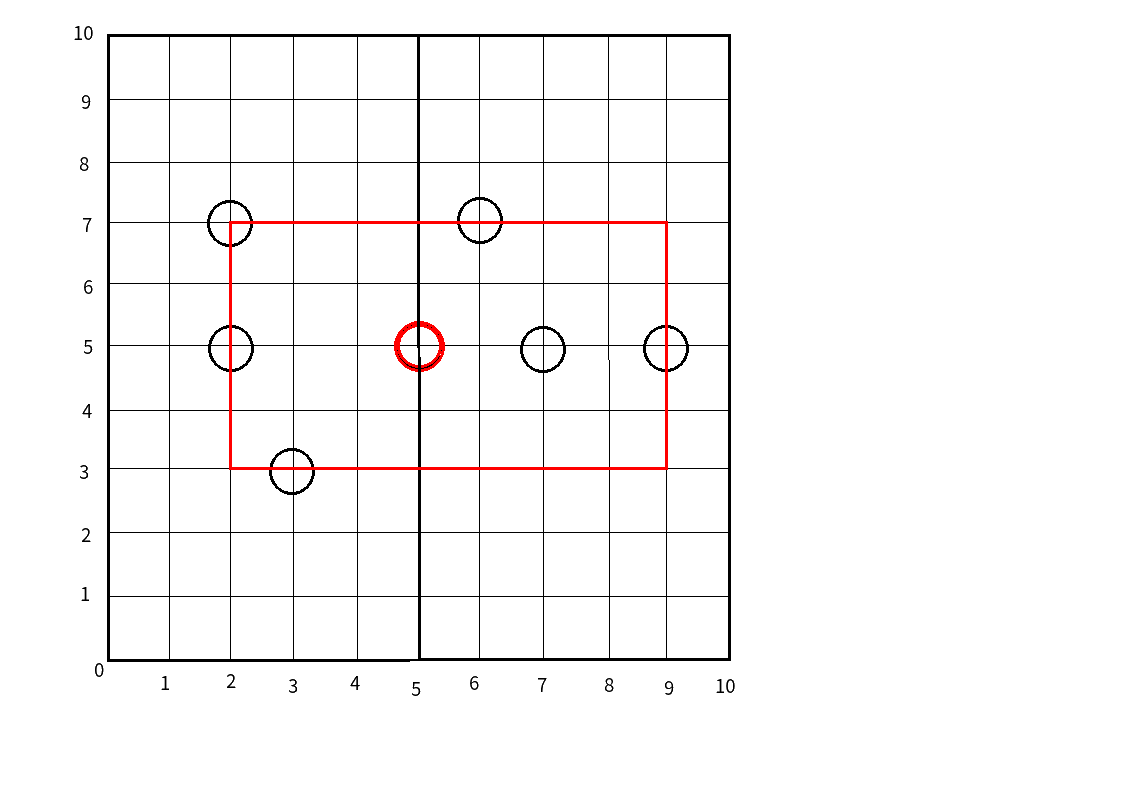
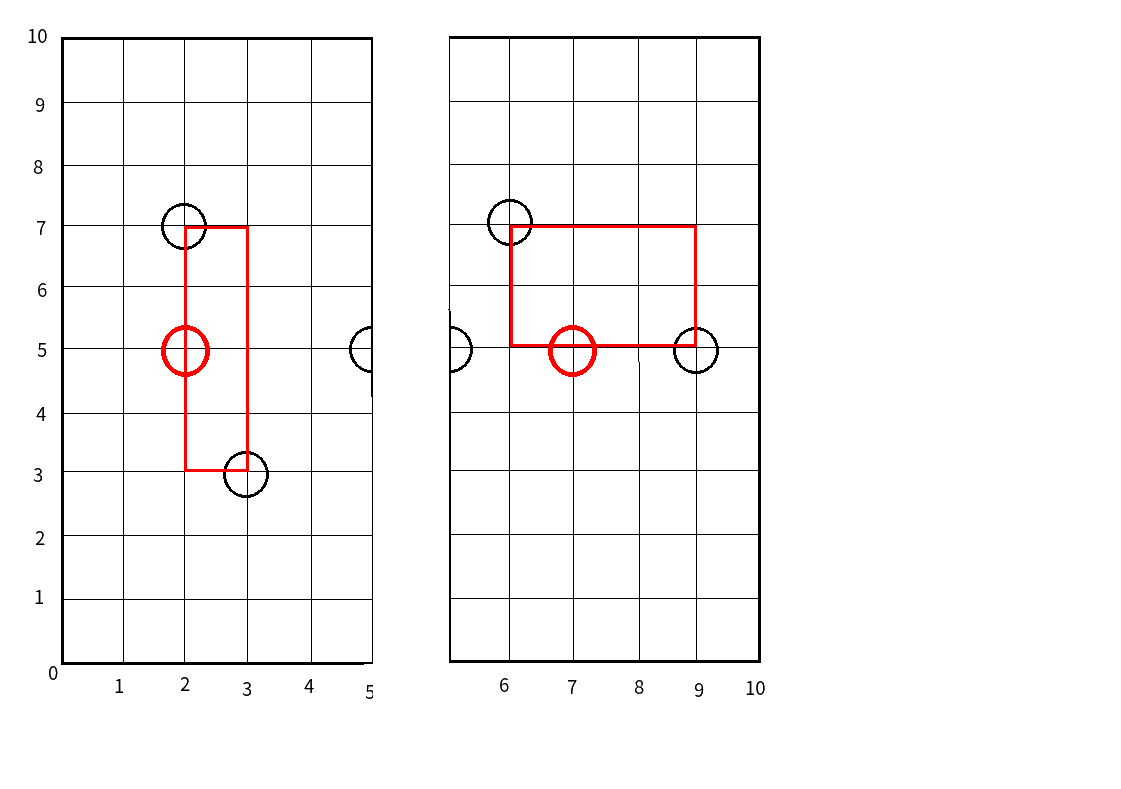
而这范围有什么用呢?
别急,讲查询的时候就知道了.
首先,我们来讲最近点(曼哈顿距离),
我们假设要查询图中离点\((4,7)\)最近的点.
(先把原图放出来,红色的为查询的点)
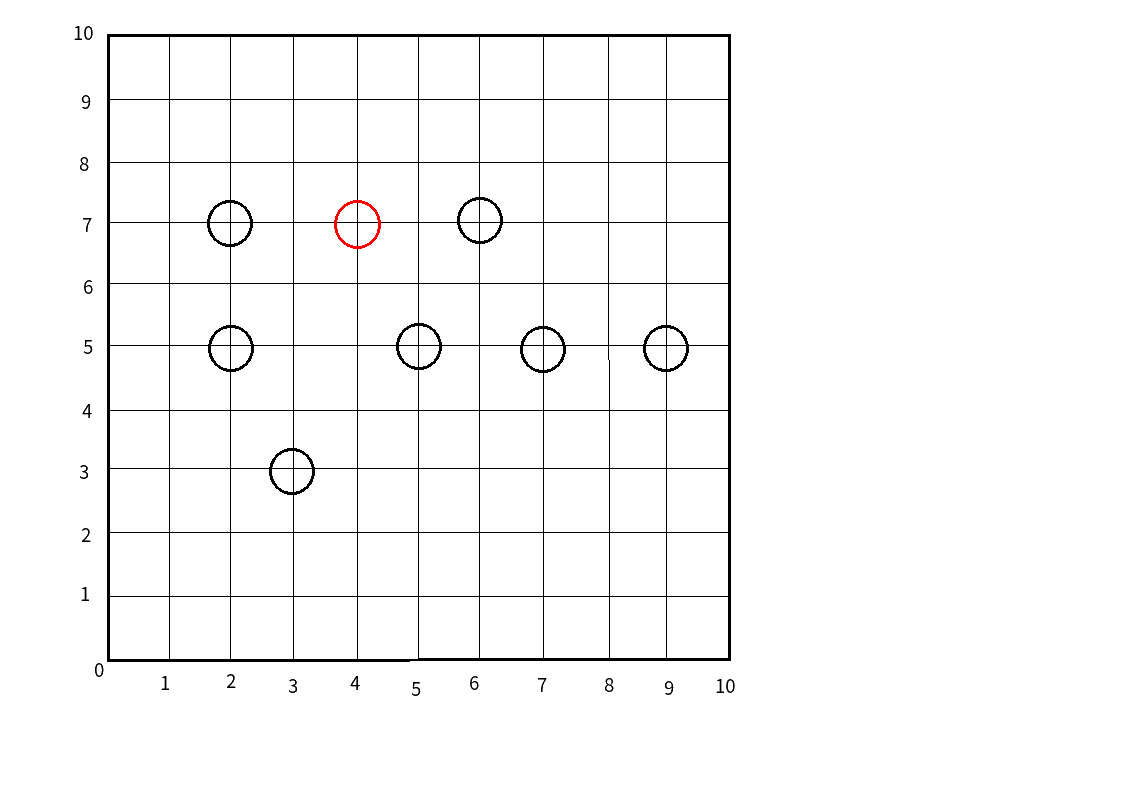
那么首先,我们找到了第一个节点(5,5),
先统计答案,
inline int dis(node a,node b){//node表示的是图中的点
return abs(a.pla[0]-b.pla[0])+abs(a.pla[1]-b.pla[1]);
}
然后我们计算到它两个儿子的范围的最短距离.
因为可能答案就在儿子的子树中,因此我们计算的是到达范围的最短距离(而不是到达儿子本身)
这时候,\(mx\)和\(mi\)就有用了,
inline int getdis(node a,int p){//p是子树节点的编号
int ret=0;
for(int i=0;i<=1;i++) ret+=max(0,a.pla[i]-t[p].mx[i])+max(0,t[p].mn[i]-a.pla[i]);
return ret;
}
如果最短距离都大于等于\(ans\)的话,那这棵子树就没必要搜了.
另外,由于kd-tree的本质是搜索+剪枝,
因此,我们可以在查询的时候,先搜索最短距离短的子树,
因为\(ans\)会在搜索时更新,
所以说不定在搜完一棵后另一棵就会被减掉了.
然后,查询的代码就出来了:
inline void query(node ret,int p){
ans=min(ans,dis(ret,t[p].place));
int teml=INF,temr=INF;
if(t[p].ls) teml=getdis(ret,t[p].ls);
if(t[p].rs) temr=getdis(ret,t[p].rs);
if(teml<temr){
if(teml<ans) query(ret,t[p].ls);
if(temr<ans) query(ret,t[p].rs);
}
else{
if(temr<ans) query(ret,t[p].rs);
if(teml<ans) query(ret,t[p].ls);
}
}
step 4
讲完了查询,我们来讲插入吧.
其实这就和BST一样啦.
一直比较到空节点在插入就行啦.
inline void insert(node ret,int &p,int opt){
if(!p){p=New();t[p].place=ret;t[p].ls=t[p].rs=0;update(p);return ;}
if(ret.pla[opt]<=t[p].place.pla[opt]) insert(ret,t[p].ls,opt^1);
else insert(ret,t[p].rs,opt^1);
update(p);check(p,opt);
}
然而,会有一件细思极恐的事情:
在插入多了后,我们的树可能会退化成一条链!
所以,我们要利用替罪羊树的思想,
设一个值\(\alpha=0.75\)(当然想设其它的也可以),
当某点的\(size*\alpha\)小于它某棵子树的\(size\)时,就直接拍扁重建.
\(size\):终于想起我了
而代码也很简单:
inline int New(){
if(top) return sta[top--];//这下知道什么意思了吧(拍扁重建时直接返回节点就好)
return ++tot;
}
inline void pia(int p,int cnt){//有声音的代码[滑稽]
if(t[p].ls) pia(t[p].ls,cnt);//cnt表示已经存了多少个点了
a[cnt+t[t[p].ls].size+1]=t[p].place,sta[++top]=p;//拍扁后用一个栈来存节点
if(t[p].rs) pia(t[p].rs,cnt+t[t[p].ls].size+1);
}
inline void check(int &p,int opt){//判断是否需要重建
if(t[p].size*alpha<t[t[p].ls].size||t[p].size*alpha<t[t[p].rs].size)
pia(p,0),p=build(1,t[p].size,opt);
}
那么到这里,kd-tree就基本讲完啦!
step 5
来看例题吧:洛谷P4169 [Violet]天使玩偶/SJY摆棋子
这题就是板子了(当然也可以用CDQ分治写).
上代码吧:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define INF 0x3f3f3f3f
using namespace std;
inline int read(){
int sum=0,f=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c<='9'&&c>='0'){sum=sum*10+c-'0';c=getchar();}
return sum*f;
}
const double alpha=0.75;
struct node{int pla[2];}a[2000001];
struct tree{int mx[2],mn[2],size,ls,rs;node place;}t[2000001];
int n,m,rt,tot,now,ans;
int sta[2000001],top=0;
inline int New(){
if(top) return sta[top--];
return ++tot;
}
bool cmp(node a,node b){return a.pla[now]<b.pla[now];}
inline void update(int p){
for(int i=0;i<=1;i++){
t[p].mx[i]=t[p].mn[i]=t[p].place.pla[i];
if(t[p].ls) t[p].mx[i]=max(t[p].mx[i],t[t[p].ls].mx[i]),t[p].mn[i]=min(t[p].mn[i],t[t[p].ls].mn[i]);
if(t[p].rs) t[p].mx[i]=max(t[p].mx[i],t[t[p].rs].mx[i]),t[p].mn[i]=min(t[p].mn[i],t[t[p].rs].mn[i]);
}
t[p].size=t[t[p].ls].size+t[t[p].rs].size+1;
}
inline int build(int l,int r,int opt){
if(l>r) return 0;
int x=New(),mid=(l+r)>>1;now=opt;
nth_element(a+l,a+mid,a+r+1,cmp);t[x].place=a[mid];
t[x].ls=build(l,mid-1,opt^1);t[x].rs=build(mid+1,r,opt^1);
update(x);return x;
}
inline void pia(int p,int cnt){
if(t[p].ls) pia(t[p].ls,cnt);
a[cnt+t[t[p].ls].size+1]=t[p].place,sta[++top]=p;
if(t[p].rs) pia(t[p].rs,cnt+t[t[p].ls].size+1);
}
inline void check(int &p,int opt){
if(t[p].size*alpha<t[t[p].ls].size||t[p].size*alpha<t[t[p].rs].size)
pia(p,0),p=build(1,t[p].size,opt);
}
inline void insert(node ret,int &p,int opt){
if(!p){p=New();t[p].place=ret;t[p].ls=t[p].rs=0;update(p);return ;}
if(ret.pla[opt]<=t[p].place.pla[opt]) insert(ret,t[p].ls,opt^1);
else insert(ret,t[p].rs,opt^1);
update(p);check(p,opt);
}
inline int getdis(node a,int p){
int ret=0;
for(int i=0;i<=1;i++) ret+=max(0,a.pla[i]-t[p].mx[i])+max(0,t[p].mn[i]-a.pla[i]);
return ret;
}
inline int dis(node a,node b){return abs(a.pla[0]-b.pla[0])+abs(a.pla[1]-b.pla[1]);}
inline void query(node ret,int p){
ans=min(ans,dis(ret,t[p].place));
int teml=INF,temr=INF;
if(t[p].ls) teml=getdis(ret,t[p].ls);
if(t[p].rs) temr=getdis(ret,t[p].rs);
if(teml<temr){
if(teml<ans) query(ret,t[p].ls);
if(temr<ans) query(ret,t[p].rs);
}
else{
if(temr<ans) query(ret,t[p].rs);
if(teml<ans) query(ret,t[p].ls);
}
}
int main(){
n=read();m=read();
for(int i=1;i<=n;i++) a[i].pla[0]=read(),a[i].pla[1]=read();
rt=build(1,n,0);
for(int i=1;i<=m;i++){
int opt=read();node ret;
ret.pla[0]=read();ret.pla[1]=read();
if(opt==1) insert(ret,rt,0);
else if(opt==2) ans=INF,query(ret,rt),printf("%d\n",ans);
}
return 0;
}
可能还会更新(埋坑)...


 浙公网安备 33010602011771号
浙公网安备 33010602011771号