题解 【NOIP2006】作业调度方案

【NOIP2006】作业调度方案

Description

我们现在要利用 m 台机器加工 n 个工件，每个工件都有 m 道工序，每道工序都在不同的指定的机器上完成。每个工件的每道工序都有指定的加工时间。
每 个工件的每个工序称为一个操作，我们用记号 j-k 表示一个操作，其中 j 为 1 到 n 中的某个数字，为工件号； k 为 1 到 m 中的某个数字，为工序号，例如 2-4 表示第 2 个工件第 4 道工序的这个操作。在本题中，我们还给定对于各操作的一个安排顺序。
例 如，当 n=3 ， m=2 时，“ 1-1 ， 1-2 ， 2-1 ， 3-1 ， 3-2 ， 2 -2 ” 就是一个给定的安排顺序，即先安排第 1 个工件的第 1 个工序，再安排第 1 个工件的第 2 个工序，然后再安排第 2 个工件的第 1 个工序，等等。
一方面，每个操作的安排都要满足以下的两个约束条件。
(1) 对同一个工件，每道工序必须在它前面的工序完成后才能开始；
(2) 同一时刻每一台机器至多只能加工一个工件。
另一方面，在安排后面的操作时，不能改动前面已安排的操作的工作状态。
由于同一工件都是按工序的顺序安排的，因此，只按原顺序给出工件号，仍可得到同样的安排顺序，于是，在输入数据中，我们将这个安排顺序简写为“ 1 1 2 3 3 2 ” 。
还要注意，“安排顺序”只要求按照给定的顺序安排每个操作。不一定是各机器上的实际操作顺序。在具体实施时，有可能排在后面的某个操作比前面的某个操作先完成。
例如，取 n=3,m=2 ，已知数据如下：

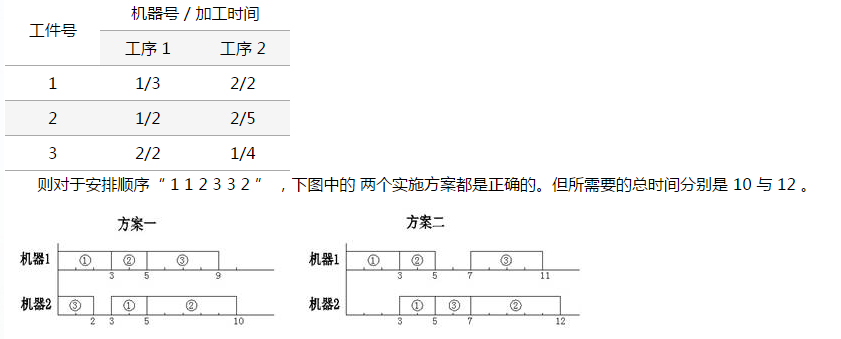
当 一个操作插入到某台机器的某个空档时（机器上最后的尚未安排操作的部分也可以看作一个空档），可以靠前插入，也可以靠后或居中插入。为了使问题简单一些， 我们约定：在保证约束条件（ 1 ）（ 2 ）的条件下，尽量靠前插入。并且，我们还约定，如果有多个空档可以插入，就在保证约束条件（ 1 ）（ 2 ）的条件下，插入到最前面的一个空档。于是，在这些约定下，上例中的方案一是正确的，而方案二是不正确的。
显然，在这些约定下，对于给定的安排顺序，符合该安排顺序的实施方案是唯一的，请你计算出该方案完成全部任务所需的总时间。

Input

第 1 行为两个正整数，用一个空格隔开：m n（其中 m （ <20 ）表示机器数， n （ <20 ）表示工件数）
第 2 行： m * n个用空格隔开的数，为给定的安排顺序。
接下来的 2n 行，每行都是用空格隔开的 m 个正整数，每个数不超过 20 。
其中前 n 行依次表示每个工件的每个工序所使用的机器号，第 1 个数为第 1 个工序的机器号，第 2 个数为第 2 个工序机器号，等等。
后 n 行依次表示每个工件的每个工序的加工时间。
可以保证，以上各数据都是正确的，不必检验。

Output

只有 一个正整数，为最少的加工时间。

Sample Input

2 3
1 1 2 3 3 2
1 2
1 2
2 1
3 2
2 5
2 4

Sample Output

10

Hint

Source

NOIP2006
贪心 ， 模拟

解析

一开始看这题似乎挺难的。。

后来仔细读题，

好像直接模拟就行了。

再看数据范围，

直接简单粗暴地用暴力。

结果就AC了。

 

贴AC代码：

#include <bits/stdc++.h>
using namespace std;

int n,m;
int a[1001][2]/*顺序*/,sum[1001]/*第i件工件目前的工序*/;
int ma[1001][1001]/*第i件第j道的机器*/,ti[1001][1001]/*第i件第j道的时间*/;
int f[101][10001]/*机器*/,ans,d[101][101];

int main(){
    scanf("%d%d",&m,&n);
    for(int i=1;i<=n*m;i++){
        scanf("%d",&a[i][0]);
        a[i][1]=++sum[a[i][0]]/*当前是第几道工序*/;
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            scanf("%d",&ma[i][j]);
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            scanf("%d",&ti[i][j]);
        }
    }
    for(int i=1;i<=n*m;i++){
        int x=a[i][0]/*工件*/,y=a[i][1]/*工序*/;
        int p=ma[x][y]/*机器*/,q=ti[x][y]/*时间*/;
        int k=d[x][y-1]+1,cnt=0;
        while(1){
            if(f[p][k]==0) cnt++;
            else cnt=0;
            if(cnt==q) break;
            k++;
        }/*寻找最前面的满足时间的空档*/
        d[x][y]=k/*x件y道完成的时间*/;
        ans=max(ans,k);
        for(int j=0;j<q;j++){
            f[p][k-j]=1;
        }
    }
    printf("%d\n",ans);
    return 0;
}