《程序员面试金典》+《算法导论》

《程序员面试金典》+《算法导论》 

　　因为最近可能会面临一波面试，但是自己各种算法以及常见的问题的熟悉程度感觉还不够，但是由前几次的代码优化经验来看，算法优化可以说是代码优化的重中之重，算法选取恰当往往会导致运行时间呈现多个数量级的下降，一直认为算法才是人类文化的结晶。因此此周就找了一本程序员面试的书籍配合算法导论阅读。最后看了算法导论的排序与一些图算法与面试书的考题简介。

---

琐碎细节

　　因为面试并不是单纯知识能力的体现，更是一个人综合素养的体现，面试官的印象会受到你言行举止甚至穿衣搭配的影响，前文大概就是对这些琐碎细节进行了一些交代，甚至对于合适的发邮件的时间，如何拒绝offer都进行了交代，这些还是需要注意的，花了点时间随便看了看。

技术细节

　　基本上分了数组字符串处理，栈与队列，树与图，位运算，递归与动态规划进行讲解，最后还讲了一些语言方面的知识点（C,C++,JAVA),以及一些线程锁的知识。下面顺着来捋一下，顺便补充上一些算法导论上看到的知识。

1 数组与字符串

　　面试书上包括链表，哈希表，普通数组，讲了一个快行指针的技巧。

1. 算法导论上，这部分主要讲解的是字符串匹配算法，介绍了四种，最普通的，Rabin-Karp算法，利用有限自动机，最后是经典的kmp算法。应用上，此类算法可以用于提高输入法联想的响应速度包括搜索DNA序列中的特定序列衡量标准有预处理时间与匹配时间。其中KMP算法最为巧妙，将与预处理时间降低到O(m),并将实际的匹配时间控制到了O（n）。
2. 哈希表，通过计算使得链表法散列实现的查找效率降到O(1+C),C为负载系数，使得开放查找法O(1/(1-c))，算法导论中对其进行了证明，并对如何选择合适的哈希函数提出了建议，比如除法散列法可以选择一个不接近2的整数次幂的素数作为除数，乘法散列法可以选择（sqrt（5）-1）/2产生小数部分，另外还介绍了全域散列法，并给出了一个构造方法，可惜我没学过数论，并没有看懂，也下定决心大四一定要补一些cs的基础课。实现上可以利用链表或者数组，前者更被推荐，负载系数可以大于1，通过槽位拉链处理冲突，后者负载系数已更改小于1，通过线性探测，双重散列（这里还介绍了将第二次hash仅仅产生奇数而除数为偶实现互素的小技巧）之类的方法处理冲突。

2 栈与队列

　　面试书上讲了java实现队列与栈，并讲述了几道算法题目，比较有意思的是一道用一个数组实现三个栈的题目，要求三个栈是动态的即空间是动态的，想了一段时间，但是只要注意合适的搬移与压入的时候允许循环，即应当把整个数组看成前后相连的。

3 树与图

　　当初学数据结构的时候就觉得这部分知识点复杂琐碎，几个树遍历的非递归算法几乎都写不出来，但是递归又总是面临爆栈的风险，借此再复习了一下。 面试书中基本就还是回顾了一些基本知识点，然后是题目，做了几道，其中一道在一棵节点数巨大的二叉树中查找子树的题目很有趣，算法思路是两个树完全相同与先序遍历与中序遍历相同等价（注意条件为树必须除根外度都为2，缺少左右孩子应该置空）否则会出现下面的情况，

 

 

 

 

 

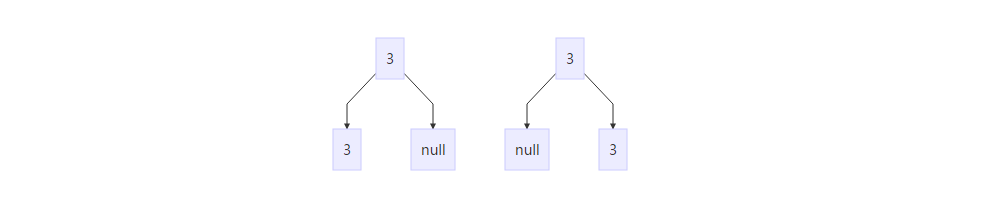
　　判定为相同的树，之后化为了字符串匹配问题，但是这种方法必然会占用大量的内存，因为要做遍历储存遍历结果，有时候这是难以忍受的，另一种方法是直接搜索较大的树，一旦碰到有相同的根节点则对两棵树进行匹配。

　　算法导论上关于这部分就太多了，树主要讲解二叉搜索树以及其插入删除，并对其平均时间复杂度做出了证明。
更多的是关于图的讨论，图的链表表示以及邻接矩阵表示，图的两种遍历，深度优先以及广度优先。并各自对其应用做了简单介绍。

• BFS搜索可以用来建立每个从一个节点开始到每个节点的最短路径，直觉上可以这么想，BFS是以开始节点为圆心，一圈一圈的扩展搜索的，实现上，只要牢记其中队列来保证访问的层次应该就能写出来.
• 关于深度优先遍历，重点讲了两个时间，第一是个是第一次访问到的时间v.d，另一个是其下所有子孙访问结束后的时间d.f,其后的许多算法都基于这个时间展开。

1. 判别节点关系，只要[v.d,v.f]这个区间与其他节点存在包含关系，则说明其中一个另一个的子孙。
2. 进行回路检测 3 . 进行拓扑排序(有向无环图)，按结束时间在链表头进行插入。
3. 查找强连通分量。这个算法感觉十分巧妙，具体的证明花费了大量的篇章，思想上可以这么理解，首先将强连通分量塌缩成一个节点，不同的强联通分量必然只有单向边，称塌缩后的图为分量图，分量图就必然是有向无环图，之后定义塌缩点的.f与.d为强联通分量中的.f的最大值与.d的最小值,其中分量图的边与塌缩点的.f息息相关，就是边指向的塌缩点的.f一定比边发出的塌缩点.f要小，那么先遍历一遍图，那么.f最大的点一定在分量图中拓扑排序的最后一个，按.f的倒序开始DFS遍历图的转置，即G所有边转向，其必然不能跑到其他强联通分量，否则不可能为一个独立的强联通分量，以此倒退，就找到了所有的强连通分量。 最后作者提出一个问题，假如按第一次访问.f的增序直接访问图，是不是也是正确的，假如正确岂不是可以省去求图的转置的时间（一般为O(V+E)),其实不是这样的，.f与分量图的拓扑排序是一致的，但是.d不是，比如思考这样的情况，

 

 

 

 

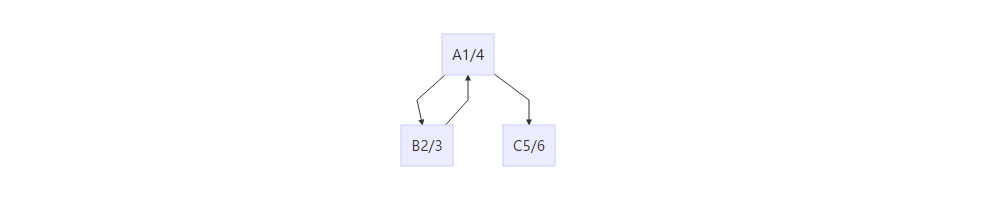
　　从A开始遍历，先走B，假如按上述算法，.f最小值为B，从B遍历则ＡＢＣ为强连通分量，显然错误，这是因为联通分量的.f最小值1与分量图的边的走向是没有确定关系的！！！！

总结

　　比较高深的图算法以及排序，动态规划还没有好好看，感觉确实是没有修过离散数学与图论，看起来有点点吃力，能看完的话会再放到一篇读书笔记里面。

　　算法真的很有意思，就是有点费脑子，尤其是算法导论的证明比较晦涩，看了一周多，觉察到一个比较功利的看法，先看算法的应用，感兴趣再看实现，然后思考大体的逻辑，如果觉得很对（比如BFS做最短路径计算以及回路检测），就不必关心它的证明。，假如真的完全不理解为什么这种算法是对的（比如利用DFS找寻强连通分量），就要仔细看证明，一般顺着证明过程来就能理清其中的逻辑，还能加深理解。最后唯一不足的是时间有限没来得及写算法的实现，感觉还是要抽空写一下的。