基环树

基环树

概念

基环树就是一棵树上多出一条边。也就是说，有 \(N\) 个点 \(N\) 条边的连通图叫做基环树。

对于有向图和无向图，分为有向基环树和无向基环树。有向基环树又分为内向基环树（每个节点以自己为起点的边只有一条）和外向基环树（每个节点以自己为终点的边只有一条）。

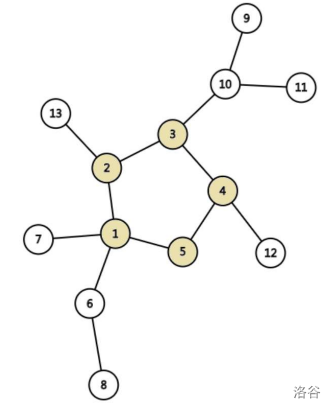
无向基环树：

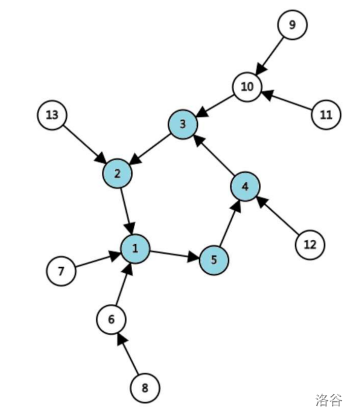
内向基环树：

外向基环树：

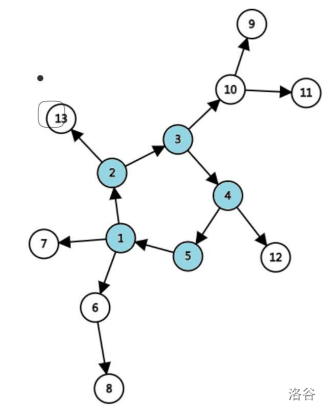
如果我们把环上的任意一条边断掉，那么这个图就会变为一棵树。如果把这个环全部断掉，这个图就会变为一个森林。

例题

[P2607 ZJOI2008] 骑士

首先，这个题非常类似于 没有上司的舞会。我们将每个骑士向他讨厌的人连边，这将会是一个基环树森林。对于每一棵基环树而言，如果他是一棵树，那么就和 没有上司的舞会 完全一样，一个简单的树形 dp。那么我们考虑断掉还上的一条边，分别以断边的两个端点为根跑树形 dp，那么这棵基环树的答案便是 \(\max(f_{u,0},f{v,0})\)。

#include <bits/stdc++.h>
#define int long long 

using namespace std;

int read() {
	int x = 0; char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') {
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x;
}
const int N = 1e6 + 10;
int n, a[N], w[N];
struct edge {
	int y, id;
}; 
vector<edge> G[N];
int vis[N], inst[N], u, v, id;
void dfs(int x, int fr) {
	if (vis[x]) return;
	vis[x] = 1;
	inst[x] = 1;
	for (edge i : G[x]) {
		int y = i.y;
		if (i.id == fr) continue;
		if (inst[y]) {
			u = x, v = y, id = i.id;
			continue;
		}
		dfs(y, i.id);
	}
	inst[x] = 0;
}
int f[N][2];
void dp(int x, int fr) {
	f[x][1] = w[x];
	f[x][0] = 0; 
	for (edge i : G[x]) {
		int y = i.y;
		if (i.id == fr) continue;
		if (i.id == id) continue;
		dp(y, i.id);
		f[x][1] += f[y][0];
		f[x][0] += max(f[y][1], f[y][0]);
	}
}
signed main() {
	n = read();
	for (int i = 1; i <= n; i++) {
		w[i] = read(), a[i] = read();
		G[i].push_back({a[i], i});
		G[a[i]].push_back({i, i});
	}
	int ans = 0;
	for (int i = 1; i <= n; i++) {
		if (vis[i]) continue;
		dfs(i, 0);
		dp(u, 0);
		int val = f[u][0];
		dp(v, 0);
		ans += max(val, f[v][0]);
	}
	printf("%lld\n", ans);
	
	return 0;
}

Others

这边有一个对于外向树用拓扑排序找环的小技巧：

for (int i = 1; i <= n; i++) {
    v[i] = read();
    G[v[i]].push_back(i);
    in[v[i]]++;
}
for (int i = 1; i <= n; i++) {
    if (in[i] == 0) q.push(i);
}
while (!q.empty()) {
    int y = q.front(); q.pop();
    tag[y] = 1;
    int x = v[y];
    // 此处可以进行一些其他的操作，比如转移
    in[x]--;
    if (in[x] == 0) q.push(x);
}