在n×n的棋盘上放置n个不能互相捕捉的国际象棋“皇后”的所有布局。这是来源于国际象棋中的一个问题。皇后是棋盘上最具杀伤力的一个棋子,她可以捕捉与她在同一行,或同一列,或同一斜线(有两条)上的所有棋子。如下图所示,红线经过的格子都会被皇后捕捉。
1. 问题描述:
在n×n的棋盘上放置n个不能互相捕捉的国际象棋“皇后”的所有布局。这是来源于国际象棋中的一个问题。皇后是棋盘上最具杀伤力的一个棋子,她可以捕捉与她在同一行,或同一列,或同一斜线(有两条)上的所有棋子。如下图所示,红线经过的格子都会被皇后捕捉。

2. 问题分析:
1) 皇后的杀伤力在她所对应的行,列,和两条斜线上,所以应该满足该皇后所在的行、列和两条斜线都不存在其它皇后。
2) 所以为了避免皇后冲突,一个可行的办法是将棋盘上所有的行,列,和斜线的占用状态分别用数组存起来,初始状态为未占用。在每成功放入一个皇后以后,将该皇后所对应的行,列,和两条斜线的状态更新为占用。在每次尝试将某个皇后放置到某个位置的时候,需要检查该位置所对应的行,列,和斜线的占用状态,只有全部未被占用,才可以将该皇后放到该位置。
3) 接下来的问题有两个:一是如何用数组来存储棋盘上所有的行,列,和斜线的占用状态?二是对棋盘上每一个位置如何找到它所对应的行、列和斜线在状态数组中的位置。以下分行、列、左低右高斜线和左高右低斜线四种情况来讨论:
4) 行:对n×n的棋盘有n行(1 ~ n),用一个n + 1维的数组row[n + 1](row[0]不用)来表示每一行的占用状态。位置(i,j)对应的行的占用状态为row[i]。
5) 列:对n×n的棋盘有n列(1 ~ n),用一个n + 1维的数组col[n + 1](col[0]不用)来表示每一列的占用状态。位置(i,j)对应的列的占用状态为col[j]。
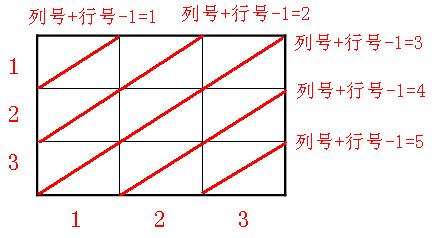
6) 左低右高斜线:n×n的棋盘总共有2n – 1条左低右高斜线,所以可以用2n维的数组b[2n](b[0]不用)来存储每一条左低右高斜线的占用状态。。对某一条斜线,其特点是它所经过的每一个格子的(列号 + 行号)相等,所以可以用这个值作为数组下标来唯一标记每一条左低右高斜线,为了使下标从1开始,对所有的下标减1。如下图所示。位置(i,j)对应的左低右高斜线的占用状态为b[i + j – 1]。
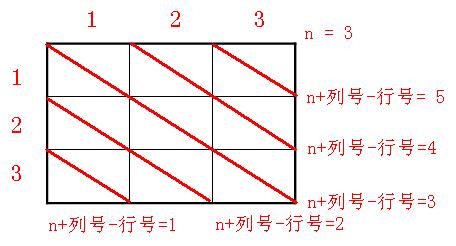
7) 左高右低斜线:n×n的棋盘总共有2n – 1条左高右低斜线,所以可以用2n维的数组c[2n](c[0]不用)来存储每一条左高右低斜线的占用状态。。对某一条斜线,其特点是它所经过的每一个格子的(列号 – 行号)相等,所以可以用这个值作为数组下标来唯一标记每一条左高右低斜线,为了避免出现负值,将所有的下标值都加上一个n。如下图所示。位置(i,j)对应的左高右低斜线的占用状态为c[n + j - i]。
3. 解题思路:
1) 要将n个皇后放到n×n的棋盘中,则每一列必须且只能放一个皇后。所以问题转化为确定皇后在每一列中的位置(在第几行上)。
2) 从第一列开始,依次考察每一列。
3) 在考察每一列的时候,总是从第一行开始,尝试将皇后放入,如果可以放入,就接着考察下一列的第一行。如果不可以放入,就接着考察这一列的下一行,直到成功,然后接着考察下一列的第一行。
4) 如果这一列的每一行都不可以放入,说明这一列前面各列的皇后放置有问题,导致这一列无法放入,需要回溯。
5) 回溯的时候,如果前面的一列每一行都已经被尝试过了,就需要接着往前回溯,直到找到还有行未被尝试过的列,然后尝试这一列的下一行。
6) 在回溯过程中经过的每一列都需要将已经放入的皇后取出来,以备后面重新选择位置放入。
7) 如果每一列都被考察完毕,即每一列中的皇后都找到了合适的位置,则找到一个解。
8) 在找到一个解后,如果还要寻找其它解,则需要回溯,尝试其它情况。
9) 当回溯到第0列时,说明1 ~ n列的所有行都已经被尝试过了,没有其它情况可以尝试,结束程序。
4. 代码:

 Code
Code
void QueenLayout(int n)
{
int j;
char next;
int* row = new int[n + 1]; //每一行的状态(是否已经被占用:0 - 未被占用,1 - 被占用)。
int* col = new int[n + 1]; //皇后在每一列中的位置(行号)
int* b = new int[2 * n]; //每一条正斜线(左低右高)的状态(是否已经被占用:0 - 未被占用,1 - 被占用)。
int* c = new int[2 * n]; //每一条反斜线(左高右低)的状态(是否已经被占用:0 - 未被占用,1 - 被占用)。
bool occupied = false; //用于判断在每一列中放置皇后时,她所对应的行和两条斜线,是否至少有一条已经被占用。
int m = 1; //当前被考察的列
col[0] = col[1] = 1; //从第一列开始的第一行开始考察,如果可以就考察第二列的第一行,如果不可以就考察第一列的第二行(即col[1] = 2)
//初始化所有的行为未被占用状态
for (j = 0; j <= n; j++)
{
row[j] = 0;
}
//初始化所有的斜线为未被占用状态
for (j = 0; j < 2*n; j++)
{
b[j] = c[j] = 0;
}
do
{
if (!occupied)
{
//已经考察到第n列,所以一次考察完毕。
if (m == n)
{
//打印找到的一个解
cout << "Column\tRow\n";
for (j = 1; j <= n; j++)
{
printf("%3d\t%d\n", j, col[j]);
}
//是否接着寻找下一个解
cout << "Find next solution? (Y/N)\n";
cin >> next;
if (next != 'Y' && next != 'y')
{
return;
}
//已经找到一个解,回溯找下一个解。
//一直回溯到还有行未被考察过的列
while(col[m] == n)
{
m--;
//在回溯过程中经过的每一列都需要将已经放入的皇后取出来,以备后面重新选择位置放入。
row[col[m]] = b[m + col[m] - 1] = c[n + m - col[m]] = 0;
}
//考察这一列的下一行
col[m]++;
}
else
{
//因为occupied==false,所以皇后可以被放在当前考察列的当前考察行
//将该皇后对应的行和两条斜线置为被占用状态
row[col[m]]=b[m + col[m] - 1] = c[n + m - col[m]] = 1;
//考察下一列的第一行
col[++m] = 1;
}
}
else
{
//因为occupied==true,所以皇后不可以被放在当前考察列的当前考察行
//一直回溯到还有行未被考察过的列
while(col[m] == n)
{
m--;
//在回溯过程中经过的每一列都需要将已经放入的皇后取出来,以备后面重新选择位置放入。
row[col[m]] = b[m+col[m] - 1] = c[n + m - col[m]] = 0;
}
//考察这一列的下一行
col[m]++;
}
//考察皇后是否可以被放在当前考察列的当前考察行,即她对应的行和两条斜线是否全部未被占用
occupied = row[col[m]] || b[m + col[m] - 1] || c[n + m -col[m]];
}while (m != 0);//退到m == 0, 表示 1 ~ n 列的所有行都被考察过了,即考察过了所有可能的情况,整个考察过程结束。
delete []row;
delete []col;
delete []b;
delete []c;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号