【详解】并查集高级技巧:加权并查集、扩展域并查集
一、普通并查集
可以理解为使用数组实现的树形结构,只保存了每个节点的父节点(前驱)。
功能为:合并两个节点(及其所在集合) 、 查找节点所属集合的代表节点(可以理解为根节点)。
原理及用法
以6个元素为例(编号0到5):把0单独划分为一个集合;把1,2,3,4划分为一个集合;把5单独划分为一个集合。
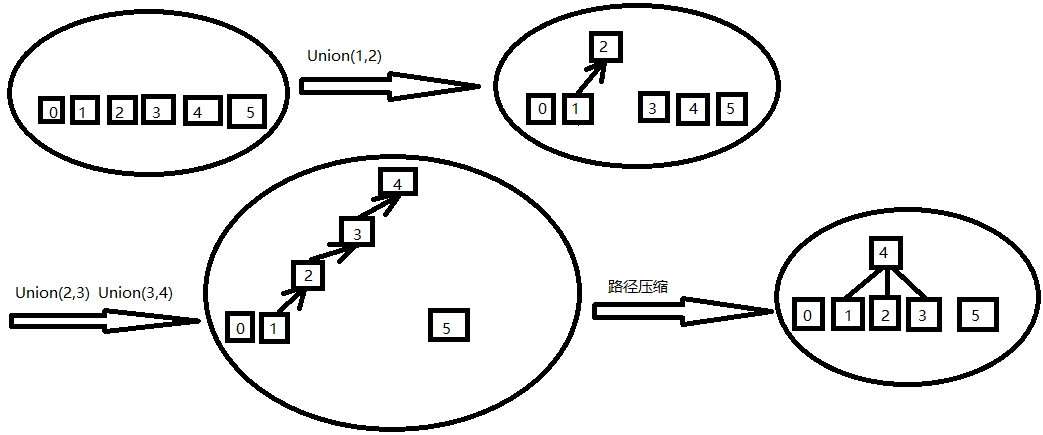
1. 初始化 init()
n个元素的并查集,只需要一个容量为n的数组f[n],值全部初始化为自己即可:for(int i=0;i<n;i++) f[i]=i;
2. 查找节点所属集合 Find(x)
主要代码:Find(x): if(x == f[x]) return x;
return Find(f[x]);
但若只是简单的这样做,会出现上图第三个圆中的情况,即查找某个节点时递归太多次。因此需要“路径压缩”,只需增加一步:
Find(x): if(x == f[x]) return x;
return f[x] = Find(f[x]);
3. 合并两个节点(及其所在集合) Union(x, y)
Union(x,y): int fx=Find(x), fy=Find(y);
if(fx != fy) f [fx] = fy; // 此处换为f [fy] = fx也行,道理相同,意义和效果其实也一样。
注意:一定是f [fx] = fy,而不是f [x] = y。只有把x和y的最终父节点(前驱)连接起来,所属的两个集合才算真正完全连通,整个逻辑也才能正确。
二、扩展域并查集
使用情景:
n个点有m对关系,把n个节点放入两个集合里,要求每对存在关系的两个节点不能放在同一个集合。问能否成功完成?
思路:
把每个节点扩展为两个节点(一正一反),若a与b不能在一起(在同一个集合),则把a的正节点与b的反节点放一起,把b的正节点与a的反节点放一起,这样就解决了a与b的冲突。若发现a的正节点与b的正节点已经在一起,那么说明之前的某对关系与(a,b)这对关系冲突,不可能同时满足,即不能成功完成整个操作。
具体实现:
1. 初始化 init()
n个点,每个点扩展为两个点(一正一反),则需要一个容量为2*n的数组f[n],值全部初始化为自己即可:for(int i=0;i<2*n;i++) f[i]=i;
(注意初始编号,若编号为[1,n],则初始化应该为:for(int i=1;i<=2*n;i++) f[i]=i;)
一个点x的正点编号为x,反点编号为x+n(这样每个点的反点都是+n,规范、可读性强、不重复、易于理解)。
2. Find(x)和Union(x, y)不需要修改,含义和实现不变。
3. 解决问题的算法步骤
1)初始化2*n个节点的初始父节点,即它本身。
2)遍历m对关系,对每对(a,b),先找到a和b的父节点,若相等则说明(a,b)的关系与之前的关系有冲突,不能同时解决,则得到结果:不能完成整个操作。
否则执行:Union(a, b+n), Union(b, a+n). (这时已经Find过了,直接执行f [fx] = fy这一句就等效与Union(x, y) )
3)若m对关系都成功解决,则得到结果:能够完成整个操作。
拓展:
由于扩展域会直接使数组容量翻倍,所有一般只解决这种“二分”问题,只扩展为2倍即可。
优点在于:结构简单,并查集的操作也不需要做改变,非常易于理解。 缺点显然就是:需要额外存储空间。
三、加权并查集
使用情景:
N个节点有M对关系(M条边),每对关系(每条边)都有一个权值w,可以表示距离或划分成多个集合时的集合编号,问题依然是判断是否有冲突或者有多少条边是假的(冲突)等。
思路:
给N个节点虚拟一个公共的根节点,增加一个数组s[n]记录每个节点到虚拟根节点的距离,把x,y直接的权值w看为(x,y)的相对距离。
Union(x,y,w)时额外把x,y到虚拟根节点的距离(s值)的相对差值设置为w;Find(x)时,压缩路径的同时把当前s值加上之前父节点的s值,得到真实距离。
具体实现:
1. 初始化 init()
f[n]数组记录节点的父节点,s[n]数组记录节点到虚拟根节点的距离: for(int i=0;i<n;i++) { f[i]=i; s[i]=0; }
2. Find(x)
if(x==f[x])return x;
int t = f[x];
f[x] = Find(f[x]);
s[x] += s[t];
// s[[x] %= mod; 若s[x]表示划分成mod个集合时的集合编号等情况时,则需要求余。
return f[x];
3. Union(x, y,w)
int fx = Find(x), fy = Find(y); //此时已经s[x]和s[y]都已经计算为真值。
if(fx != fy) {
f [fx] = fy;
s [fx] = (s[x] - s[y] + w + mod) % mod;
}
4. 解决问题的算法步骤
初始化后,遍历m对关系:若x,y的父节点不同,则Union(x,y,w);否则,若x与y的差值为w,则说明正确,继续遍历,不为w时说明出现冲突。
当s[x]只是代表划分为mod个集合时的集合编号时,应该比较s[x]与s[y]的值是否相同,相同时说明出现冲突;不相同时说明之前已经解决了,正确可继续遍历。
拓展:加权并查集主要得赋予并理解s[x]值的意义,较难掌握且应用广泛
牛客网例题:关押罪犯 https://ac.nowcoder.com/acm/problem/16591 ,里面的题解和讨论区有更多讲解和入门题目链接
直接百度搜素“加权并查集”也可找到更多讲解和入门题目链接。
牛客网关押罪犯的题解代码:

#include<cstdio> #include<algorithm> using namespace std; const int maxn = 20002; const int maxm = 100002; struct edge { int a, b, c; }e[maxm]; bool cmp(edge a, edge b) { return a.c > b.c; } int f[2 * maxn]; int Find(int x) { if (x == f[x])return x; return f[x] = Find(f[x]); } int main() { int n, m; scanf("%d%d", &n, &m); for (int i = 0; i < m; i++) scanf("%d%d%d", &e[i].a, &e[i].b, &e[i].c); sort(e, e + m, cmp); //按仇恨值从大到小排序 for (int i = 1; i <= 2 * n; i++)f[i] = i; //初始化并查集 int i; //从大到小依次把每对罪犯安排到不同监狱 for (i = 0; i < m; i++) { int a = Find(e[i].a), b = Find(e[i].b); if (a == b)break; //两人的正点已在同一个集合,无法解决,最大冲突出现 f[a] = Find(e[i].b + n); //把a和b的反点(敌人)合并 f[b] = Find(e[i].a + n); //把b和a的反点(敌人)合并(每个点都有一个正点和反点) } if (i == m)printf("0"); else printf("%d", e[i].c); return 0; }

#include <iostream> #include <vector> #include <algorithm> using namespace std; typedef long long ll; const int maxn = 200000 + 10; const int gxs = 2; //模2就只有0,1两个值,分别代表两个不同的集合 const int mod = 2; int n, m; int f[maxn], s[maxn]; //f记录父节点(前驱),s记录到虚拟root点的距离 void init() { for (int i = 0; i < maxn; i++) f[i] = i, s[i] = 0; } //查找 int finds(int x) { if (x == f[x]) return x; int t = f[x]; f[x] = finds(f[x]); s[x] += s[t]; //s[x]原来是与t的相对距离,现在是与root的相对距离 s[x] %= gxs; //s值求余后代表所属监狱(二选一) return f[x]; } //新建关系 void unions(int x, int y, int w) { int fx = finds(x), fy = finds(y); if (fx != fy) { f[fy] = fx; s[fy] = s[x] - s[y] + w + gxs; //相对距离设置为w,解决这一对冲突 s[fy] %= mod; //求余直接赋予实际意义:所属的mod个集合的编号 } } struct node { int a, b; ll val; bool operator < (const node &a)const { return val > a.val; } }; vector<node> que; int main() { cin >> n >> m; int a, b; ll v; for (int i = 0; i < m; i++) { cin >> a >> b >> v; que.push_back(node{ a,b,v }); } sort(que.begin(), que.end()); //从大到小排序 init(); for (int i = 0; i < m; i++) { a = que[i].a; b = que[i].b; v = que[i].val; if (finds(a) == finds(b)) { //在同一个集合就不能直接解决冲突 if (s[a] == s[b]) { //若s值相同就说明已经在同一个集合,冲突无法解决 cout << v << endl; //因为从大到小遍历,第一个解决不了的关系的val就是答案:最小化的最大冲突值 return 0; } //否则说明解决之前的冲突后,当前冲突也被解决。 } else { //不在一个集合就可以通过设置s值解决冲突 unions(a, b, 1); } } cout << 0 << endl; return 0; }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号