第 1 讲高等数学—元素和极限（万门大学）

高等数学--元素和极限

实数的定义

戴德金分划：

将全集Q分为A、B两个集合，使得AUB = Q（实数） 并且 A∩B = Φ（空集） 并且 a∈A，b∈B，有a<b 。

实数的定义：

有理分化：

1、A中存在最大值，B中没有最小值

2、A中不存在最大值，B中有最小值

无理分化：

3、A中不存在最大值，B中不存在最小值

 实数性质：

1、稠密性（实数轴不再衍生出新数轴）

2、有序性（任何两个实数可以比大小）

分化可以比大小，所以实数可以比大小

单调有界序列存在极限（引理1）

 

实数的元素个数

自然数N  整数Z  有理数Q  实数R

势：集合元素的个数

等势：A、B集合间的元素可一一对应

 

命题一：自然数个数 = 整数个数

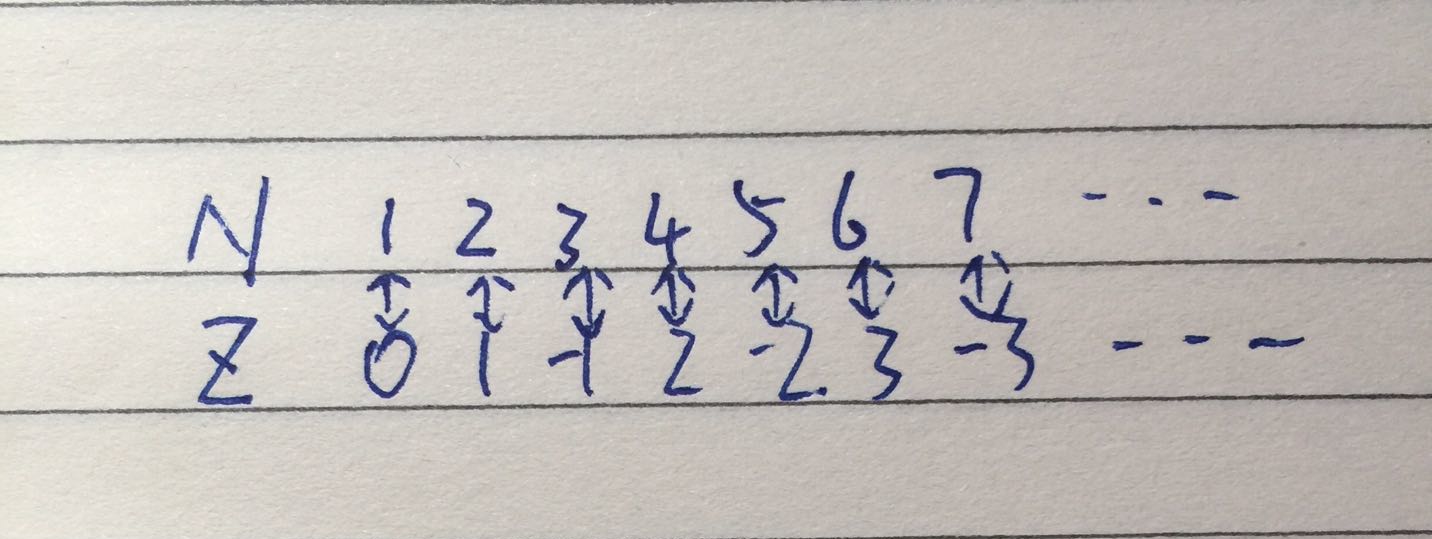
命题二：整数个数 = 有理数个数

自然数个数少于实数个数

 

无穷大的比较

 

 级数的收敛

极限的定义

序列极限/函数极限

想要任意近，只要足够近

极限的四则运算

极限的复合

极限的连续性