「洛谷P7729」交通运输(Wormhole Transportaion) 题解
本文网址:https://www.cnblogs.com/zsc985246/p/17407035.html ,转载请注明出处。
前言
很好的一道题目,有很大的难度,但是也很锻炼思维。
2023/5/18update:修正了 sub4 中的公式,更改了部分描述。
2023/5/19update:添加了代码。
2023/5/27update:日常修锅。
传送门
题目大意
有 个点和 个点对,你需要构造一张 条边的无向图,使得 个点对间最短路之和最小。
求最小值及取到最小值的方案数。
。
保证所有无序对 两两不同,且至少存在一种合法的方案。
| subtask | 特殊限制 | |
|---|---|---|
| 无 | ||
| , | ||
| 由 为无向边的图是仙人掌森林 | ||
| 由 为无向边的图是杏仁 | ||
| 无 |
仙人掌森林:每条边在至多一个简单环中的无向图。
杏仁:恰好存在两个度数大于 的结点,其他结点度数都等于 ,且所有环都经过两个度数大于 的结点的连通无向图。
思路
称以 为无向边的图为 ,我们构造的图为 。
定义 “删去” 表示这条边或路径在 中,但不在 中。“保留” 表示这条边或路径既在 中也在 中。
令 表示在 中 到 的最短路。
求解最短路最小值
题目中保证至少存在一种合法的方案,那么我们可以知道, 中一定有环。
若 中无环,那么 就是普通森林,对于任意森林里的一棵树 ,令其有 条边, 个节点。
由于 有 个节点,所以我们要使其连通至少需要 条边。那么我们所需的总边数为 ,大于题目要求的 ,所以不存在合法方案,矛盾。
那么我们就可以猜测,最短路最小值与环有关。
设环内边数量为 。
先考虑环外的边。
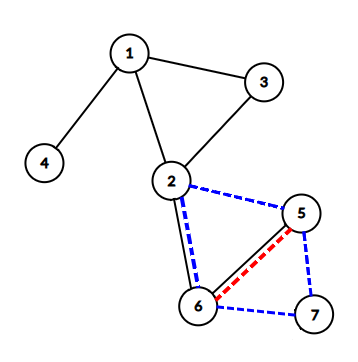
我们观察不在 的环上的边 。
假设我们选择了一个中转点进行连边。
可以发现,如果我们选择一个不在 中的中转点 ,那么我们会连接 两条边,,使用两条边。但实际上我们可以连接 ,此时 且只使用了一条边。
所以,我们不会选择不在 中的节点作中转。
同样的,如果我们选择一个在 中的中转点 ,那么我们会连接 两条边,,使用两条边。但如果我们连接 ,,同样使用两条边。
所以,我们不会选择在 中的节点作中转。
综上,我们不会作中转。
也就是说,如果 ,且 不是环边,那么 。
根据这条性质,我们可以知道,环外的边的答案就是 。
接下来考虑环内的边。
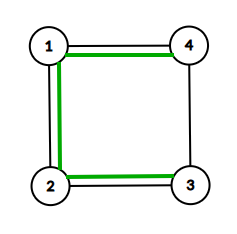
我们假设这个环长度为 。
显然,如图所示将环断成一条链最优。答案为 。
那如果有多个环?显然我们只需断一个环。而又因为我们要让答案最小,即选择一个环 使 最小,所以 一定是最小环。
我们设最小环的长度为 ,那么最后的答案就是 。
这样我们就算出了总答案为 。
关于最小环环长,我们只需要求出 的最短路 和 的第一条路与最短路不同的最短路 ,然后枚举每对距离为 的点对 ,取 的最小值即为环长。
sub2
是一个大小为 ,编号顺次为 的环。
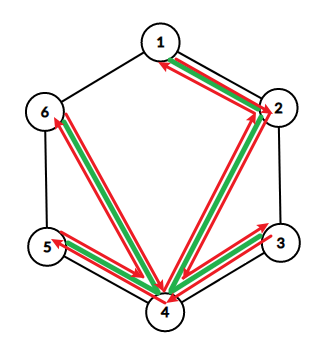
此时 是一棵树,我们令 的根节点为 。
我们只需要计算使 成立的 的个数。
可以发现, 的和实际上就是 的路径长,而 代表每条边正好经过两次。如上图红色路径所示。
那么这样的路径实际上就是我们 dfs 的遍历过程,也就是说我们进入了一棵子树之后会遍历完内部的所有点后再出来。
所以任意一个子树内所有节点的编号必定连续。
我们推广到环上编号不连续的情况,即对于任意一个子树内所有节点的编号组成的集合 ,一定存在环上一段路径,使得这段路径上节点的编号组成的集合与 相同。下方称此结论为条件 。
然后考虑如何计数。
我们设在 中, 的儿子中编号最大的是 ,子树 中点的编号是 。
不难发现,除去子树 后的树编号是 ,也满足条件 ,是一个子问题。
但因为 不是 中编号最大的点,所以它不是子问题。但是如果我们将它拆分成 和 两个区间,我们发现,这两个区间都是满足条件 的,都是子问题。
那么我们就把答案拆分成了三个子问题:。
而不是 是因为 是 的儿子, 这条边一定存在。
发现区间的左右端点对答案没有影响,所以设 表示长度为 的连续区间的方案数。
那么答案 。
因为我们钦定了根节点为 ,所以不会算重。
至于具体计算,用 辅助就可以达到 。
sub3
是仙人掌森林。
那么我们只需要找出最小环的个数 ,然后将最小环的答案乘上 就好了。
注意不是乘方,时刻牢记我们只断一个环。
sub4
是杏仁。
题目中说,杏仁是恰好存在两个度数大于 的结点,其他结点度数都等于 ,且所有环都经过两个度数大于 的结点的连通无向图。
我们翻译一下: 中有两个点 ,它们之间有 条不交路径,如下图。我们设这些路径长度从小到大依次为 。
显然最小环的长度 ,数量 也好算,但是我们不能用 乘以数量来计算答案,因为会算重。
思考什么时候会算重。
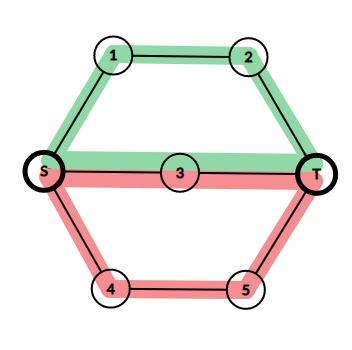
如图,我们令绿色的环为 ,红色的环为 ,路径 为 , 为 , 为 。
发现保留路径 ,改变 与保留路径 ,改变 的方案有一部分是重复的。
据此,我们定义 表示长度为 和 的路径构成的最小环中,保留路径 且 两条路径之间没有连边的方案数。那么对于上图情况,最后答案就是 。
拓展到整个图,令长为 的路径个数为 ,长为 的路径个数为 :
- 当 时,答案为 。
- 当 时,答案为 。
现在只需要考虑怎么计算 了。这里同样钦定一个点是根节点。我们不需要知道根节点具体是谁。
可以发现与条件 差别不大,可以推出 。
发现其实与 无关,所以直接定义 为只更改最小环上长度为 的路径的方案数。
其实仔细观察一下就能发现,这个递推式跟 sub2 中给出的解决 预处理问题的 一模一样。所以我们直接计算 和 就可以了。
sub6
没有特殊限制。
我们类比 sub4 的解法,定义一个 被图 中的环 影响,当且仅当所有不在 上的 ,且存在 。
如果 被 影响,那么 只能在 中 相交的路径 上作修改得到。
那么对于求解方案,我们可以找到 上的一段区间 ,长度为 ,然后只对 进行改动。
发现这与我们 数组的定义很像。但是要注意的是,这里 的端点所连的边也都会改动,所以我们要做一个容斥,答案是 。
但是其实可以发现,对于 只被一个环 影响时,我们无法完全计算到它的贡献。因为多个环的相交部分一定不大于 。
设 为组成最小环的路径,其中 与 均构成最小环。
如果相交部分 ,那么 ,即 ,同理 。
此时发现 ,即 ,与 为最小环长的定义矛盾。
那么我们就需要统计 只被一个环 影响的部分答案。
那么我们只需要进行一个容斥即可。我们用总方案 减去只包含长度小于等于 的路径的方案 。
我们令在 中 表示 到 的最短路。
那么首先我们需要找出最小环长度 和数量 ,然后将 数组和 数组计算出来。
接下来我们枚举每个路径 ,即枚举路径的端点 ,注意需要保证 。对答案的贡献为 。
最后用容斥统计 只被一个环 影响的部分答案。
然后将单个最小环的答案乘上 ,按 sub4 的方法去重就好了。
分析时间复杂度。
处理两点之间最短路、两点之间第一条路与最短路不同的最短路(代码注释中称为次短路),用 bfs 可以做到 。
处理最小环信息,直接做就好,复杂度 。
数组与 数组。复杂度 。
枚举路径计算答案是 。
总时间复杂度 。
那么终于,这道题结束了。
代码实现
本代码需要吸氧。也可以把 long long 改成 int 卡常。
#include<bits/stdc++.h>
#define ll long long
#define For(i,a,b) for(ll i=(a);i<=(b);++i)
#define Rep(i,a,b) for(ll i=(a);i>=(b);--i)
#define pb push_back
const ll N=2e3+10;
const ll p=1e9+7;
using namespace std;
ll ksm(ll a,ll b){ll res=1;while(b){if(b&1)res=res*a%p;a=a*a%p;b>>=1;}return res;}
ll n,m,sid;
vector<ll>e[N];//图G
//下方称次短路为i到j的第一条边与最短路不同的最短路
ll dis[N][N];//dis[i][j]:i到j的最短路
ll dis2[N][N];//dis2[i][j]:i到j的次短路
ll num[N][N];//num[i][j]:i到j的次短路的条数
ll tmp[N][N];//tmp[i][j]:从i到终点s第一条边是(i,j)的最短路条数
ll cnt=1e9,tot;//cnt:最小环长度 tot:最小环数量
void bfs(ll s){//处理dis和dis2
//s是最短路终点
//从终点向外拓展,以便寻找最短路的第一条边
For(x,1,n)for(ll y:e[x])tmp[x][y]=0;//清空
queue<pair<ll,ll>>q;//第二个信息表示上一个点,0表示不是第一次加入队列,需取次短路计算
q.push({s,n+1});
dis[s][s]=0;
while(q.size()){
ll x=q.front().first,pre=q.front().second;
q.pop();
ll d=pre?dis[x][s]+1:dis2[x][s]+1;//距离
for(ll y:e[x]){
if(y==pre)continue;
ll res=1;
if(!pre)res=(num[x][s]-tmp[x][y]+p)%p;//从x到s不经过边(x,y)的最短路条数
if(d<dis[y][s]){//bfs距离单调不减,所以此时一定是第一次更新到起点y
dis[y][s]=d;
q.push({y,x});//y第一次加入队列
}else if(d<dis2[y][s]){//不是第一次更新点y,所以处理次短路
dis2[y][s]=d;
num[y][s]=res;
tmp[y][x]=res;
q.push({y,0});
}else if(d==dis2[y][s]){//次短路长度相同,更新数量
num[y][s]=(num[y][s]+res)%p;
tmp[y][x]=res;
}
}
}
}
ll f[N],g[N];//定义同思路
ll h[N];//提前记录容斥的式子
void init(){//预处理,dis、dis2、cnt、tot、f和g
For(x,1,n)For(y,1,n)dis[x][y]=dis2[x][y]=1e9;
For(x,1,n)bfs(x);//处理dis、dis2和num
//枚举两个距离为1的点,计算cnt和tot
For(x,1,n){
for(ll y:e[x]){
if(x<y){
if(dis2[x][y]+1<cnt)cnt=dis2[x][y]+1,tot=num[x][y];
else if(dis2[x][y]+1==cnt)tot=(tot+num[x][y])%p;
}
}
}
tot=tot*ksm(cnt,p-2)%p;//去重,因为每个最小环上都有cnt个距离为1的点对
//处理f和g
f[1]=g[1]=1;
For(i,2,n+1){
For(j,1,i-1)f[i]=(f[i]+g[j]*f[i-j])%p;
For(j,1,i)g[i]=(g[i]+f[j]*f[i+1-j])%p;
}
//这里直接把g[i]-2*g[i-1]+g[i-2]处理出来了
For(i,1,n){
h[i]=(g[i]-2*g[i-1]+2*p)%p;
if(i>1)h[i]=(h[i]+g[i-2])%p;
}
}
void mian(){
scanf("%lld%lld%lld",&n,&m,&sid);
For(i,1,m){
ll x,y;
scanf("%lld%lld",&x,&y);
e[x].pb(y),e[y].pb(x);
}
init();//预处理
ll ans=0;
For(x,1,n){
For(y,x+1,n){
if(dis[x][y]+dis2[x][y]==cnt){//能构成最小环
ans=(ans+h[dis[x][y]])%p;
if(dis[x][y]==dis2[x][y])ans=(ans+h[dis[x][y]]*num[x][y])%p;
}
}
}
//大于cnt/2的情况
ll res=f[cnt];
For(i,1,cnt/2)res=(res-cnt*h[i]%p+p)%p;
ans=(ans+tot*res)%p;
printf("%lld\n%lld",m+cnt-2,ans);
}
int main(){
int T=1;
// scanf("%d",&T);
while(T--)mian();
return 0;
}
尾声
如果你发现了问题,你可以直接回复这篇题解
如果你有更好的想法,也可以直接回复!




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 25岁的心里话
· 按钮权限的设计及实现