Codeforces Round #831 (Div. 1 + Div. 2) 题解
本文网址:https://www.cnblogs.com/zsc985246/p/17086280.html ,转载请注明出处。
比赛题目非常有趣,推荐!
I 题暂时没有代码,后面可能会补。
2023/2/7update:更新 G 题题解和 I 题思路。
传送门
Codeforces Round #831 (Div. 1 + Div. 2)
A.Factorise N+M
题目大意
多组测试。每次输入一个质数 $ A $,输出任意一个使 $ A + B $ 不是质数的 $ B $。
注意 $ B ≠ 1 $。
思路
直接输出 $ n $。
代码实现
#include<bits/stdc++.h>
#define ll long long
#define For(i,a,b) for(ll i=(a);i<=(b);++i)
#define Rep(i,a,b) for(ll i=(a);i>=(b);--i)
const ll N=1e6+10;
using namespace std;
ll n;
void mian(){
scanf("%lld",&n);
printf("%lld\n",n);
}
int main(){
int T=1;
scanf("%d",&T);
while(T--)mian();
return 0;
}
B.Jumbo Extra Cheese 2
题目大意
你有 $ n $ 个长方形,大小是 $ a_i \times b_i $,现在你需要把它们放到一起,可以旋转,求周长最小值。
思路
构造题。把所有的长方形的最短边作为底边,然后直接按高度排列,答案就是 $ 2\ \times $ 每个长方形最短边之和 $ +\ 2\ \times $ 所有长方形中的最长边。
代码实现
#include<bits/stdc++.h>
#define ll long long
#define For(i,a,b) for(ll i=(a);i<=(b);++i)
#define Rep(i,a,b) for(ll i=(a);i>=(b);--i)
const ll N=1e6+10;
using namespace std;
ll n,m;
ll a[N],b[N];
void mian(){
ll ans=0,maxx=0;
scanf("%lld",&n);
For(i,1,n){
scanf("%lld",&a[i]);
scanf("%lld",&b[i]);
ans+=min(a[i],b[i])*2;
maxx=max(maxx,max(a[i],b[i]));
}
ans+=maxx*2;
printf("%lld\n",ans);
}
int main(){
int T=1;
scanf("%d",&T);
while(T--)mian();
return 0;
}
C.Bricks and Bags
题目大意
给定 $ n $ 个石头和三个空背包,将 $ n $ 个石头放入三个背包中。从三个背包中拿出三个石头,假设拿出的石头的质量分别是 $ a,b,c $,分数就是 $ |a-b|+|b-c| $,你需要使最终的分数的最小值最大。输出分数最小值的最大可能值。
思路
先把所有的石头排序。可以发现中间的背包摆放的石头必定是一段前缀或一段后缀。枚举断点计算极值即可。
代码实现
#include<bits/stdc++.h>
#define ll long long
#define For(i,a,b) for(ll i=(a);i<=(b);++i)
#define Rep(i,a,b) for(ll i=(a);i>=(b);--i)
const ll N=1e6+10;
using namespace std;
ll n,m;
ll a[N],b[N];
void mian(){
ll ans=0;
scanf("%lld",&n);
For(i,1,n){
scanf("%lld",&a[i]);
}
sort(a+1,a+n+1);
//一段前缀
For(i,1,n-2){
ans=max(ans,a[i+1]-a[i]+a[n]-a[i]);//一边放最大值,一边放i+1
}
//一段后缀
For(i,3,n){
ans=max(ans,a[i]-a[1]+a[i]-a[i-1]);//一边放最小值,一边放i-1
}
printf("%lld\n",ans);
}
int main(){
int T=1;
scanf("%d",&T);
while(T--)mian();
return 0;
}
D.Knowledge Cards
题目大意
你有一个 $ n \times m $ 的棋盘,在 $ (1,1) $ 处有 $ n \times m $ 个棋子,从上到下第 $ i $ 个棋子标号为 $ a_i $,你的目标是将所有棋子按照 $ 1-n $ 的顺序移到 $ (n,m) $ 处。你可以将每个格子中顶端的棋子向任意方向移动一步。$ (1,1) $ 处只能移出棋子,而 $ (n,m) $ 处只能移入棋子。除了 $ (1,1) $ 和 $ (n,m) $ 处,不能在一格中堆叠多个棋子。
如果可以将所有棋子按顺序移到 $ (n,m) $,输出YA,否则输出TIDAK。
思路
手动模拟放的过程。可以发现只要棋盘中除了 $ (1,1) $ 和 $ (n,m) $ 有其它空位,就可以将任意一个不在 $ (1,1) $ 和 $ (n,m) $ 的棋子移动到 $ (n,m) $。所以只要场上同时存在不少于 $ n \times m - 2 $ 个棋子即无解。
代码实现
#include<bits/stdc++.h>
#define ll long long
#define For(i,a,b) for(ll i=(a);i<=(b);++i)
#define Rep(i,a,b) for(ll i=(a);i>=(b);--i)
const ll N=1e6+10;
using namespace std;
ll n,m,k;
ll a[N];
ll vis[N];
void mian(){
ll ans=0;
scanf("%lld",&n);
scanf("%lld",&m);
scanf("%lld",&k);
For(i,1,k){
scanf("%lld",&a[i]);
vis[i]=0;
}
ll limit=n*m-3;
ll pos=k;
ll cnt=0;
For(i,1,k){
if(cnt<limit){
if(a[i]==pos){
pos--;
while(vis[pos]){
pos--;
cnt--;
}
}else{
vis[a[i]]=1;
cnt++;
}
}else{
printf("TIDAK\n");
return;
}
}
printf("YA\n");
}
int main(){
int T=1;
scanf("%d",&T);
while(T--)mian();
return 0;
}
E.Hanging Hearts
题目大意
给定一棵 $ n $ 个节点的树,每次操作可以选择一个叶子节点 $ x $,删去 $ x $,记录 $ x $ 的权值 $ w_x $。如果 $ w_x $ 比它父亲 $ y $ 的权值 $ w_y $ 小,$ w_y=w_x $。一共需要进行 $ n $ 次操作。最后得到 $ w_x $ 组成的序列。这个序列的价值是该序列的最长非下降子序列的长度。你需要对每个节点添加权值,使得价值最大。输出最大价值。
提示
-
深度越深,点权越小更优。
-
可以使用树上DP。
思路
一个节点深度越深,点权越小,这样删去它就会将父亲的权值变小,就会有更长的非下降子序列。
我们定义 $ dp_i $ 表示 $ i $ 的子树产生的最长非下降子序列的长度。
可以发现 $ dp_i $ 至少是子树的最大深度。因为我们可以先删掉其它点,只留下一条链。
所以就可以得到 $ dp_i=\sum\max(dp_j,maxd_j) $,其中 $ j $ 是 $ i $ 的儿子节点。
最后输出 $ \max(dp_1,maxd_1) $ 即可。
代码实现
#include<bits/stdc++.h>
#define ll long long
#define For(i,a,b) for(ll i=(a);i<=(b);++i)
#define Rep(i,a,b) for(ll i=(a);i>=(b);--i)
#define pb push_back
const ll N=1e6+10;
using namespace std;
ll n,m,k;
ll a[N];
ll dp[N],d[N];
vector<ll>e[N];
void dfs(ll x){
ll maxd=0;
for(ll y:e[x]){
dfs(y);
maxd=max(maxd,d[y]);
dp[x]+=max(dp[y],d[y]);
}
d[x]=maxd+1;
}
void mian(){
ll ans=0;
scanf("%lld",&n);
For(i,2,n){
ll x;
scanf("%lld",&x);
e[x].pb(i);
}
dfs(1);
printf("%lld\n",max(dp[1],d[1]));
For(i,1,n)e[i].clear();
}
int main(){
int T=1;
// scanf("%d",&T);
while(T--)mian();
return 0;
}
F.Conditional Mix
题目大意
给定 $ n $ 个一元集 $ {a_i} $ , 每次可以合并两个交集为空的集合。合并时会建立一个新集合 $ A $,元素为被合并的两个集合所有的元素。合并后原来的两个集合被删除,用新集合 $ A $ 替换。
可以经过任意次合并。设合并后每个集合的元素个数组成可重集 $ S $。求不同 $ S $ 的数量,对 $ 998244353 $ 取模。
提示
-
考虑满足什么条件的集合 $ S $ 可以被构造出来。
-
计数DP。
思路
首先发现 $ S $ 内元素个数不满 $ n $ 个可以补 $ 0 $。
考虑满足什么条件的集合 $ S $ 可以被构造出来。
首先需要满足 $ \underset{i=1}{\overset{n}{\sum}}S_i=n $。人话解释就是 $ S $ 内元素和为 $ n $。
如果我们令一个数 $ i $ 出现的次数为 $ cnt_i $,那么其实 $ S $ 还需要满足对于 $ \forall k \in [1,n] , \underset{i=1}{\overset{k}{\sum}}S_i\le\underset{i=1}{\overset{n}{\sum}}min(cnt_i,k) $。人话解释是 $ S $ 的前 $ k $ 个元素之和不能超过 $ A $ 中每个元素的出现次数与 $ k $ 的最小值之和。
为什么需要跟 $ k $ 取 $ \min $ 呢?因为题目要求合并的两个集合不能有交集。也就是说合并后的集合不会有重复元素。
这个计数组合数显然不可行,自信计数DP。
将输入的 $ a $ 数组排序,从大到小选数。设 $ f_{i,j,k} $ 表示确定了 $ S $ 中的前 $ i $ 个数,总和为 $ j $,其中选择了 $ a $ 中的最小数为 $ k $。转移方程可以参照代码。
根据上面推出的规律,$ k $ 的枚举范围可以缩小到 $ \frac{n}{i} $。空间上第一维可以滚动。
然后就做完了。
代码实现
#include<bits/stdc++.h>
#define ll long long
#define For(i,a,b) for(ll i=(a);i<=(b);++i)
#define Rep(i,a,b) for(ll i=(a);i>=(b);--i)
const ll N=2e3+10;
const ll p=998244353;
using namespace std;
ll n,m,k;
ll a[N];
ll dp[2][N][N];
ll t[N];
ll s[N];
void mian(){
ll ans=0;
scanf("%lld",&n);
For(i,1,n){
scanf("%lld",&a[i]);
t[a[i]]++;
}
sort(t+1,t+n+1);
For(i,1,n){
For(j,1,n){
s[i]+=min(i,t[j]);//前缀和
}
}
ll i0=0,i1=1;
For(i,1,n)dp[i0][0][i]=1;
For(i,1,n){
ll limit=n/i;
For(j,0,s[i]){
dp[i1][j][limit+1]=0;
}
Rep(k,limit,0){
For(j,0,s[i]){
dp[i1][j][k]=dp[i1][j][k+1];//不选k
if(j>=k){
dp[i1][j][k]+=dp[i0][j-k][k];//转移方程
if(dp[i1][j][k]>=p)dp[i1][j][k]-=p;//手动取模
}
}
}
i0^=1,i1^=1;
}
printf("%lld\n",dp[i0][n][0]);
}
int main(){
int T=1;
// scanf("%d",&T);
while(T--)mian();
return 0;
}
G.Dangerous Laser Power
题目翻译
(不是题目大意的原因是不好概括)
有一个 \(n \times m\) 的网格,上面每个位置都有一个激光发射器。每个发射器有四个面,分别编号为 \(0,1,2,3\)。如下图:
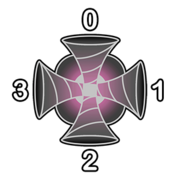
发射器有一个类型 \(t_{i,j} = 0/1\) 和一个强度 \(s_{i,j}\)。从编号为 \(x\) 的面进入、速度为 \(y\) 的激光会被发射器从编号为 \(x' = (x+2+t_{i,j}) \mod 4\) 的面发射出去,速度为 \(y' = \max\{y,s_{i,j}\}\),同时这个发射器消耗 \(y'-y\) 的能量。
现在每个发射器会向四个方向各发射一个速度为 \(1\) 的激光(不消耗能量)。一个激光超出网格或进入了 \(10^{100}\) 个发射器之后就会消失。
如果一个发射器消耗的能量总和对 \(2\) 取模等于这个发射器的类型,则这个发射器是好的。
求一种类型分配方案,使得尽可能多的发射器是好的。
提示
-
按强度依次安排类型,可以让所有发射器都是好的。
-
维护信息快速计算发射器消耗的总能量。
思路
按强度大小依次安排类型。因为激光速度如果大于发射器的强度,发射器不消耗能量。
现在我们只需要快速计算发射器消耗的总能量。
记 $ id_{i,j,k} $ 表示位置为 $ (i,j) $ 的发射器的第 $ k $ 个面的编号。
我们可以维护一个 $ sum_{i} $ 表示 $ id $ 为 $ i $ 的面接收的所有激光速度之和,$ t_{i} $ 表示 $ id $ 为 $ i $ 的面接收的激光个数。
那么位置为 $ (i,j) $ 的发射器消耗的总能量就是 $ ans = \underset{k=0}{\overset{3}{\sum}} t_{pos} \times s_{i,j} - sum_{pos} , pos=id_{i,j,k} $
这样我们就可以快速计算类型了。
接下来只需要用并查集,在加边的时候顺便更新信息。
代码实现
#include<bits/stdc++.h>
#define ll long long
#define For(i,a,b) for(ll i=(a);i<=(b);++i)
#define Rep(i,a,b) for(ll i=(a);i>=(b);--i)
const ll N=1e3+10;
using namespace std;
struct portal{
ll s;//强度
ll x,y;//坐标
bool operator<(const portal &a)const{
return s<a.s;
}
}a[N*N];//发射器
ll n,m;
ll id[N][N][5];//发射器每个面的编号
ll sum[4*N*N],t[4*N*N];//sum表示这个面进入的激光速度和,t表示进入这个面的激光个数
ll nxt[2][4*N*N];//nxt[0]表示类型为0时的下一个发射器,nxt[1]同理
ll ans[N][N];//答案
//并查集
ll fa[4*N*N];
ll find(ll x){
if(fa[x]==x)return x;
return fa[x]=find(fa[x]);
}
void add(ll x,ll y,ll z){
y=find(y);
if(!y||x==y)return;
fa[x]=y;
//更新sum和t
sum[y]=(sum[y]+t[x]*z)&1;
t[y]+=t[x];
}
void mian(){
ll cnt=0;//发射器编号
ll num=0;//发射器的面编号
scanf("%lld",&n);
scanf("%lld",&m);
For(i,1,n){
For(j,1,m){
scanf("%lld",&a[++cnt].s);
a[cnt].x=i,a[cnt].y=j;//记录坐标
For(k,0,3){
id[i][j][k]=++num;//编号
fa[num]=num;
sum[num]=t[num]=1;//最开始发射的激光
}
}
}
For(i,1,n){
For(j,1,m){
//暴力连边
nxt[0][id[i][j][0]]=id[i+1][j][0];
nxt[0][id[i][j][1]]=id[i][j-1][1];
nxt[0][id[i][j][2]]=id[i-1][j][2];
nxt[0][id[i][j][3]]=id[i][j+1][3];
nxt[1][id[i][j][0]]=id[i][j-1][1];
nxt[1][id[i][j][1]]=id[i-1][j][2];
nxt[1][id[i][j][2]]=id[i][j+1][3];
nxt[1][id[i][j][3]]=id[i+1][j][0];
}
}
sort(a+1,a+cnt+1);//按强度从小到大排序
For(i,1,cnt){
ll x=a[i].x,y=a[i].y;
//计算消耗的总能量
ll s=0;
For(k,0,3){
s+=a[i].s*t[id[x][y][k]]-sum[id[x][y][k]];
}
s&=1;
//记录答案
ans[x][y]=s;
//将激光发射出去
For(k,0,3){
add(id[x][y][k],nxt[s][id[x][y][k]],a[i].s&1);
}
}
For(i,1,n){
For(j,1,m){
printf("%lld",ans[i][j]);
}
printf("\n");
}
}
int main(){
int T=1;
// scanf("%d",&T);
while(T--)mian();
return 0;
}
H.MEX Tree Manipulation
题目大意
有一棵有根树,根节点为 $ 1 $。这棵树的叶子节点的权值为 $ 0 $,非叶子节点的权值为其儿子节点(不是整棵子树)的 $ \text{mex} $ 值。
现在这棵树只有一个根节点 $ 1 $,有 $ n $ 次操作,第 $ i $ 次操作在节点 $ x $ 下面接入一个编号为 $ i+1 $ 的节点。对于每次操作,你需要输出操作结束后所有节点的权值之和。
提示
-
可以离线处理。
-
点的权值最大可能值比较小。
-
加点只影响这个点到根节点的一条链,考虑树链剖分。
-
加入一个值,$ mex $ 只有两种情况。
思路
首先考虑离线。
我们发现题目强调了是儿子节点,考虑计算点的权值最大值。
令 $ f_i $ 表示让一个点权值为 $ i $ 至少需要的节点数。
可以推出 $ f_i=\underset{j=1}{\overset{i-1}{\sum}}f_{j} $,整理得到 $ f_i=2^i $。
即一个点的权值最大为 $ \log\ n $。
因为加点只影响这个点到根节点的一条链,一般树上的链式修改有树上差分和树链剖分两种常用优化技巧。这里需要多次输出答案,所以使用树链剖分。
具体来讲就是假设加入的是一个节点的重儿子,将当前的 $ ans $ 减去这条链的答案,然后更改之后再加回来。
考虑维护一个值 $ p_{i,j} $,表示在 $ i $ 的下面插入一个值为 $ j $ 的点后的 $ mex $ 值。
树链剖分维护链上修改需要带上线段树,思考如何在线段树上维护这个值。
因为线段树的区间按照 $ dfs $ 序排列,所以在 $ i $ 下方插入值为 $ j $ 的点等价于在 $ dfn_i $ 这个点表示的区间最后方加入一个值为 $ j $ 的点。
然而这样的时间复杂度为 $ O(n\ \log^3n) $。虽然你卡常到极致还是可以过。
因为加入一个数 $ x $,当 $ mex=x $ 时 $ mex $ 改变,否则不变,所以 $ j $ 的那一维只需要开 $ 2 $。
然后我们需要多维护一个数组 $ num_{i,0/1} $ 表示点 $ i $ 的儿子集合中前两个没有出现的权值,这样可以快速确定 $ p $ 数组的第二维的下标。
这样,时间复杂度就是 $ O(n\ \log^2n) $。
如果没有理解上面的文字,可以结合代码和注释理解!
代码实现
#include<bits/stdc++.h>
#define ll long long
#define For(i,a,b) for(ll i=(a);i<=(b);++i)
#define Rep(i,a,b) for(ll i=(a);i>=(b);--i)
#define lson rt<<1
#define rson rt<<1|1
const ll N=3e5+10;
using namespace std;
ll n;
ll ans;
ll cnt,fir[N],nxt[N],v[N];
void add(ll x,ll y){
v[++cnt]=y;
nxt[cnt]=fir[x];
fir[x]=cnt;
}
ll fa[N],dep[N],siz[N],son[N];
ll dfn_x,dfn[N],top[N];
void dfs(ll x,ll t){
top[x]=t;
dfn[x]=++dfn_x;
if(!son[x])return;
dfs(son[x],t);
for(ll i=fir[x];i;i=nxt[i]){
ll y=v[i];
if(y==son[x])continue;
dfs(y,y);
}
}
ll b[N];//标记链顶位置
ll val[N];//标记这个节点的mex值
ll vis[N][20];//标记当前节点儿子节点权值的出现情况
ll s[N<<2][2];//总和
ll p[N<<2][2];//加入一个值之后的mex
ll num[N<<2][2];//加入的值
void change(ll rt,ll l,ll r,ll x,ll z1,ll z2){
if(l==r){
//直接更改
s[rt][0]=p[rt][0]=num[rt][0]=z1;
s[rt][1]=p[rt][1]=num[rt][1]=z2;
return;
}
ll mid=l+r>>1;
if(x<=mid)change(lson,l,mid,x,z1,z2);
else change(rson,mid+1,r,x,z1,z2);
//本质是dfs序!
For(i,0,1){
ll t=p[rson][i];//假设加入p[rson][i]
p[rt][i]=p[lson][t==num[lson][0]];//加入之后继承原来的mex值
s[rt][i]=s[lson][t==num[lson][0]]+s[rson][i];//求和
}
num[rt][0]=num[rson][0];//num[lson][0]已经用过
}
ll query(ll rt,ll l,ll r,ll x,ll y,ll &z){//z用取址是因为右边的查询对左边有影响
if(x<=l&&r<=y){
ll ans=s[rt][z==num[rt][0]];//记录总和
z=p[rt][z==num[rt][0]];//记录当前mex
return ans;
}
ll ans=0;
ll mid=l+r>>1;
//这里不能写反了!一定是先走右边!
if(y>mid)ans+=query(rson,mid+1,r,x,y,z);//先查右边的mex
if(x<=mid)ans+=query(lson,l,mid,x,y,z);//用右边的mex查左边的mex
return ans;
}
void get_mex(ll x,ll &z1,ll &z2){//找前两个不为0的位置
z1=z2=19;
For(i,0,19){
if(!vis[x][i]){
if(z1==19){
z1=i;
}else{
z2=i;
break;
}
}
}
}
void insert(ll x){
ll f=fa[x];
ll z;
while(f){
z=19;//因为查询中每次都会更改z的值,所以需要初始化
ans-=query(1,1,n,dfn[top[f]],dfn[b[top[f]]],z);//减去之前贡献
f=fa[top[f]];
}
val[x]=19;
b[top[x]]=x;//动态修改标号(假设加入的是重儿子)
while(x){
ll z1,z2;
get_mex(x,z1,z2);//找到加入的值
change(1,1,n,dfn[x],z1,z2);//加入这个值
z=19;
ans+=query(1,1,n,dfn[top[x]],dfn[b[top[x]]],z);//加上现在贡献
x=top[x];
vis[fa[x]][val[x]]--;//减去原来的值
val[x]=z;//更改
vis[fa[x]][val[x]]++;//加回来
x=fa[x];
}
}
void mian(){
scanf("%lld",&n);
n++;
//由于点集输入有顺序,所以这里可以直接使用循环处理fa,dep,siz和son
dep[1]=1;
For(i,2,n){
scanf("%lld",&fa[i]);
dep[i]=dep[fa[i]]+1;
add(fa[i],i);//单向边即可
}
Rep(x,n,1){
siz[x]=1;
for(ll i=fir[x];i;i=nxt[i]){
ll y=v[i];
siz[x]+=siz[y];
if(siz[y]>siz[son[x]]){
son[x]=y;
}
}
}
//树链剖分的第二次dfs
dfs(1,1);
b[1]=1;
change(1,1,n,1,0,1);//先算出总体答案
For(i,2,n){
insert(i);//加入一个点
printf("%lld\n",ans);
}
}
int main(){
int T=1;
// scanf("%d",&T);
while(T--)mian();
return 0;
}
I.Arranging Crystal Balls
(代码没有写,有需要可以阅读下面的链接)
题目大意
给定一个 \(n\) 个点组成的环,每个点的取值范围是 \([0,m-1]\)。每次操作可以将环上一段长度为 \(k\) 的区间 \(+1\) 或 \(-1\)。点权超出取值范围会溢出。求将环变为 \(0\) 的最小操作数。
提示
-
定长区间修改可以使用差分。
-
将点分成多个独立组。
-
枚举端点变化量,断环为链。
-
设计独立组的权值。
-
背包+单调队列。
思路
设差分数组 \(b_i=(a_i-a_{(i-1) \mod n}) \mod m\)。
发现 \(a\) 全部为 \(0\) 等价于 \(a_0=0\) 且 \(b\) 全部为 \(0\)。
一次操作就等价于 \(b_i\) 和 \(b_{(i+k) \mod n}\) 分别 \(+1,-1\)。
这提示我们可以将 \(i\) 和 \(i+k\) 分到一组,形成多个相互独立的组。
可以发现组的个数是 \(cnt=\gcd(n,k)\),组的大小是 \(l=\frac{n}{cnt}\)。
一次操作就变为选择一个组内的相邻两个数(可以选择首尾)分别 \(+1,-1\)。
因为修改的区间长度为 \(k\),所以对 \(a_0\) 有影响的修改操作总个数为 \(k\)。所以每个组中对 \(a_0\) 有影响的操作个数为 \(\frac{k}{cnt}\)。
套路:一个数列需要进行相邻两个元素分别 \(+1,-1\) 操作,并需要知道操作最小数量时,前缀和可以将操作简化为前缀和数组上单点 \(+1,-1\)。但是如果数列不为负,需要保证前缀和数组单调递增。
设组内元素为 \(c_i\)。
因为组互相独立,不妨根据套路,设前缀和数组 \(s_i=s_{i-1}+c_i\)。现在我们需要断环为链。
我们可以先做 \(c_0\) 和 \(c_{l-1}\) 之间的操作。
假设我们让 \(c_0\) 变为了 \((c_0+t)\mod m\),\(c_{l-1}\) 变为了 \((c_{l-1}-t)\mod m\)。
那么新的前缀和数组就变为了 \(s'_{i}=s_{i}+t\),特别的,\(s'_{l-1}=s_{l-1}\)。
现在我们成功地将操作转化成了单点的 \(+1,-1\) 操作。
那么我们想让差分数组 \(b\) 全为 \(0\) 就转化成了让 \(s'\) 数组的每个数都是 \(m\) 的倍数。
那么最小的操作次数就是 $ \underset{i=0}{\overset{l-2}{\sum}} \min ( s'_i \mod m,m-s'_i \mod m ) $。
我们设当 \(t=0\) 时,\(a_i\) 变为了 \(a_i+\Delta\),因为每个组中对 \(a_0\) 有影响的操作个数为 \(\frac{k}{cnt}\),当我们整体加上 \(t\) 时,这些操作都会对 \(a_i\) 产生 \(-t\) 的影响。
也就是说,当 \(t \neq 0\) 时,\(a_i\) 实际上变为了 \(a_i+\Delta-\frac{kt}{cnt}\)。
发现如果一个位置对 \(a_0\) 有影响,那 \(a_0\) 的变化量跟这个位置的 \(s'\) 的变化量是相等的。
所以我们可以提前计算出 \(\Delta\) 的值,加到 \(a_0\) 上。设此时的 \(a_0\) 变为了 \(a'_0\)。
回到最初的问题。还记得另一个条件吗?我们需要使最后 \(a_0=0\)。
如果我们的 \(a'_0\) 正好为 $ \frac{k}{cnt} \times \sum t $,我们就可以正好使 $ a_0=0 $。
对于每个环,我们设每个 \(t\) 的贡献为 $ w_t=\min(t,m-t) + \underset{i=0}{\overset{l-2}{\sum}} \min ( s'_i \mod m,m-s'_i \mod m ) $,即将 \(a_0\) 变为 \(0\) 的最小操作数加上将 \(s'\) 数组的每个数都是 \(m\) 的倍数的最小操作数。
设 \(dp_i\) 表示 $ \sum t \mod m = i $ 的最小操作数,每次算出 \(w_t\) 之后用背包计入答案即可。
但是直接这样做复杂度是 \(O(cnt \times m^2)\),需要优化。
实际上,\(\min(t,m-t)\) 和 \(\underset{i=0}{\overset{l-2}{\sum}} \min ( s'_i \mod m,m-s'_i \mod m )\) 都是只有两段的分段函数,所以 \(w_t\) 可以被分成 \(O(l)\) 个等差数列。
也就是说可以使用单调队列优化。
最终复杂度为 \(O(cnt \times l \times m) = O(n \times m)\)。
代码实现
404 Not Found
尾声
如果有什么问题,可以直接评论!
都看到这里了,不妨点个赞吧!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号