「USACO5.5」矩形周长Picture

题目描述

墙上贴着许多形状相同的海报、照片。它们的边都是水平和垂直的。每个矩形图片可能部分或全部的覆盖了其他图片。所有矩形合并后的边长称为周长。

编写一个程序计算周长。

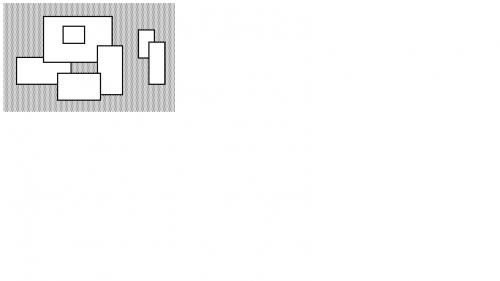
如图1所示7个矩形。

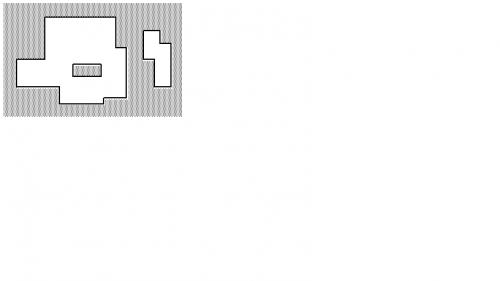
如图2所示，所有矩形的边界。所有矩形顶点的坐标都是整数。

输入输出格式

输入格式:

输入文件的第一行是一个整数\(N(0<=N<5000)\)，表示有多少个矩形。接下来\(N\)行给出了每一个矩形左下角坐标和右上角坐标（所有坐标的数值范围都在\(-10000\)到\(10000\)之间）。

输出格式:

输出文件只有一个正整数，表示所有矩形的周长。

---

基本思路

解决这一类平面矩形面积/周长并的方法，还是用最经典的方法(见下)吧。
毕竟这是一道模板题。。。
大佬们都解释了很多了，蒟蒻就不再赘述了(我才不会告诉你我不会讲)

---

扫描线\(+\)线段树

大体模板应该都差不太多:
扫描一次，从下往上，顺便记录路上的y轴方向的线段长,往\(ans\)中累加就好了。

---

细节注意事项

第一次交的时候莫名WA最后一个点，很是不解，翻了翻大佬的题解，才发现:

bool cmp(edge a,edge b){return a.h<b.h;}

这是我第一次交时写的cmp函数。

bool cmp(edge a,edge b){return a.h<b.h||(a.h==b.h&&a.f>b.f);}

这是AC时的cmp函数。

对于遇到的重合的一条上边和一条下边(当然不会在同一个矩形内)，我们优先处理下边的信息。

---

参考代码

下面就是本蒟蒻的AC代码，有什么不当或可以改进的地方欢迎大佬来指教%%%

#include<cstdio>
#include<cstdlib>
#include<algorithm>
#define rg register
using namespace std;
const int MAXN=5010;
const int MAXM=20010;
const int INF=2147483647;
inline int read(){
	int s=0;bool f=false;char c=getchar();
	while(c<'0'||c>'9')f|=(c=='-'),c=getchar();
	while(c>='0'&&c<='9')s=(s<<3)+(s<<1)+(c^48),c=getchar();
	return (f)?(-s):(s);
}
struct node{
	int l,r,cnt;
	int numx,numy;
	bool lf,rf;
}c[MAXM<<2];
#define lson rt<<1
#define rson rt<<1|1
inline void pushup(int rt){
	if(c[rt].cnt){
		c[rt].numx=c[rt].r-c[rt].l+1;
		c[rt].lf=c[rt].rf=true;
		c[rt].numy=1;
	}
	else if(c[rt].l==c[rt].r){
		c[rt].numx=0;
		c[rt].numy=0;
		c[rt].lf=c[rt].rf=false;
	}
	else{
		c[rt].numx=c[lson].numx+c[rson].numx;
		c[rt].lf=c[lson].lf;
		c[rt].rf=c[rson].rf;
		c[rt].numy=c[lson].numy+c[rson].numy-(c[lson].rf&c[rson].lf);
	}
}
inline void build(int rt,int l,int r){
	c[rt].l=l;
	c[rt].r=r;
	c[rt].cnt=0;
	c[rt].numx=0;
	c[rt].numy=0;
	c[rt].lf=false;
	c[rt].rf=false;
	if(l==r) return;
	int mid=(l+r)>>1;
	build(lson,l,mid);
	build(rson,mid+1,r);
}
inline void update(int rt,int l,int r,int v){
	if(l<=c[rt].l&&c[rt].r<=r)
		return c[rt].cnt+=v,pushup(rt);
	int mid=(c[rt].l+c[rt].r)>>1;
	if(l<=mid)update(lson,l,r,v);
	if(r>mid) update(rson,l,r,v);
	pushup(rt);
}
struct edge{int l,r,h,f;}e[MAXN<<1];
bool cmp(edge a,edge b){
	return a.h<b.h||(a.h==b.h&&a.f>b.f);
}
int main(){
	int n=read(),tot=0;
	int maxl=INF,maxr=-INF;
	for(rg int i=1;i<=n;i++){
		int x1=read(),y1=read();
		int x2=read(),y2=read();
		maxl=min(maxl,min(x1,x2));
		maxr=max(maxr,max(x1,x2));
		e[++tot]=(edge){x1,x2,y1,1};
		e[++tot]=(edge){x1,x2,y2,-1};
	}
	sort(e+1,e+tot+1,cmp);
	long long ans=0,last=0;
	build(1,maxl,maxr-1);
	for(rg int i=1;i<=tot;i++){
		update(1,e[i].l,e[i].r-1,e[i].f);
		ans+=labs(c[1].numx-last);
		ans+=(e[i+1].h-e[i].h)*2*c[1].numy;
		last=c[1].numx;
	}
	printf("%lld\n",ans);
	return 0;
}

完结撒花 \(qwq\)