sqrt函数实现

感谢杨工，让我更加认识到自己技术薄弱，这道题源自于和杨工的非正式面试，当时根本没思路，甚至没和查找有丝毫的联系，看来做自己想做的还是要付出努力的。sqrt()即开平方运算，y=x*x,已知Y的情况下求解X的值，基本的思路是找个区间，逐步计算逼近，知道需要的精度。

（1）二分查找

并不是严格的二分查找，设定寻找的区间，在这个区间中一直取中点，计算中点的平方和Y的查找，逐步逼近，直到自己需要的精度：

#define  ABS_FLOAT 0.000001
bool eqs(double val1 , double val2)
{
    double diff = fabs(val1 - val2) ;
    if(diff < ABS_FLOAT)
    {
        return true ;
    }
    else
    {
        return false ;
    }
}

//获取开方值，二分查找的方法
double SqrtBybisection(double _value)
{
    if (_value <= 0 )
        return 0 ;

    double low  = 0.0;
    double high = 0.0 ;

    if (_value > 0 && _value < 1)
    {
        low = _value;
        high = 1.0 ;
    }
    else
    {
        low  = 1.0 ;
        high =  _value  ;
    }

    double mid  = (low + high)/2.0 ;
    double last = 0.0 ;

    do 
    {
        if (mid * mid > _value)
        {
            high =  mid ;
        }
        else 
        {
            low = mid ;
        }

        last = mid ;
        mid = (high + low )/ 2.0 ;

        //std::cout << mid << std::endl ;

    }while(! eqs( last , mid)) ;

    return mid ;
}

2 牛顿迭代法

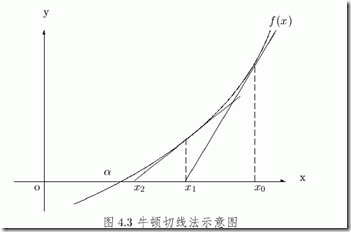
牛顿迭代法通过泰勒公司展开，通过切线逐步逼近，具体推到可以参考：牛顿逼近， sqrt实现的代码：

//牛顿迭代法求解  
/* f(x) = x^2 - v --> x = x0 - f(x0)/2x0 -->x = (x0 + v / x0) / 2  ;
   -->
*/
double SqrtByNewton(const double& _val)
{
    double nrt = _val ; 
    double last_nrt = 0 ;
     while (! eqs( nrt , last_nrt))
     {
         last_nrt = nrt ;
         nrt = (nrt + _val / nrt) / 2.0 ;
     }
     return  nrt ;
}

3 技巧算法

看到这种解法，我也很惊讶，程序员真是无底线啊~~

先看看浮点数表示，浮点数不论是float还是double在存储方式上都是遵从IEEE的规范的，float遵从的是IEEE R32.24 ,而double 遵从的是R64.53。

数学中浮点用S=M*2^N，在计算机中主要由三部分构成：符号位+指数位(N)+尾数(M)，符号位：0为正1为负，指数位：2^M ，移位存储，尾数：即有效数字，规定整数部分为1

float 浮点数内存分布：

31	30~23	22~0
1 位符号位	8位指数位	23位尾数

double型浮点内存分布：

63	62~52	51~0
1 位符号位	11位指数位	52位尾数

比如 float类型8.5，二进制表示为1000.1 ，标准表达为1.0001*2^3 , OK ,该数的指数位：127+3=130，即10000010 ，符号位 0，尾数去掉1为0001 ，填充后为0001 0000 0000 0000 0000 000，这个数的表示为 1 1000010 0001 0000 0000 0000 0000 0000 000

符号位	指数位	尾数
0	10000010	0001 0000 0000 0000 0000 000

了解这些之后，再来看一下快速的技巧：

float sqrtinv(float x)
{
    float xhalf = 0.5f*x;
    int i = *(int*)&x; // get bits for floating VALUE 
    i = 0x5f375a86- (i>>1); // gives initial guess y0
    x = *(float*)&i; // convert bits BACK to float
    x = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracy
    x = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracy
    x = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracy

    return 1/x;
}

这个算法速度据说比系统函数还要快，确实，迭代的步骤少来很多，具体解释和浮点的表示有关，可以参考下文：一般而言，一个float数据 $x$ 共32个bit，和int数据一样。其中前23位为有效数字 $M_x$ ，后面接着一个8位数据 $E_x$ 表示指数，最后一位表示符号，由于这里被开方的数总是大于0，所以我们暂不考虑最后一个符号位。此时