排序算法
排序是计算机程序设计的一种重要操作,它的功能是将一个数据元素(或记录)的任意序列,重新排列成一个按关键字有序的序列。下面主要对一些常见的排序算法做的介绍,并分析它们的时空复杂度。
常见排序算法:
1.冒泡排序
2.简单选择排序
3.直接插入排序
4.希尔排序
5.归并排序
6.快速排序
7.堆排序
常见排序算法性能的比较:
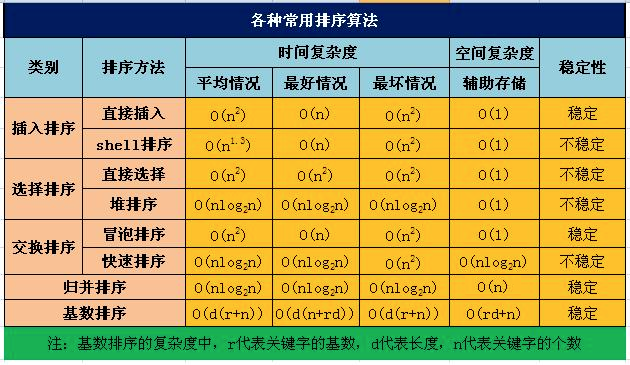
上图表中最后一列“稳定性”,是指如果在排序的序列中,存在前后相同的两个元素的话,排序前和排序后他们的相对位置不发生变化。
下面从冒泡排序开始逐一介绍:
1.冒泡排序
冒泡排序的基本思想是:设排序序列的记录个数为n,进行n-1次遍历,每次遍历从开始位置依次往后比较前后相邻元素,这样较大的元素往后移,n-1次遍历结束后,序列有序。
实现:
public class bubbleSort { //冒泡排序法 public static void main(String[] args) { int[] line = {24,36,12,25,3,67,55}; maopao(line) ; } public static void maopao(int[] line) { for (int i = 0; i < line.length - 1; i++) {// 最多做line.length-1趟排序 for (int j = i; j < line.length; j++) { int temp = 0; if (line[i] > line[j]) { //相邻的两个比较 temp = line[i]; line[i] = line[j]; line[j] = temp; } } } System.out.println(Arrays.toString(line)); //[3, 12, 24, 25, 36, 55, 67] } }
分析:最佳情况下冒泡排序只需一次遍历就能确定数组已经排好序,不需要进行下一次遍历,所以最佳情况下,时间复杂度为** O(n) **。
最坏情况下冒泡排序需要n-1次遍历,第一次遍历需要比较n-1次,第二次遍历需要n-2次,...,最后一次需要比较1次,最差情况下时间复杂度为** O(n^2) **。
2.简单选择排序
简单选择排序的思想是:设排序序列的记录个数为n,进行n-1次选择,每次在n-i+1(i = 1,2,...,n-1)个记录中选择关键字最小的记录作为有效序列中的第i个记录。
实现:
public class selectionSort { public static void main(String[] args) { int[] line = { 23, 17, 5, 8, 1, 25, 33 }; selectSort(line); } // 思路:在每步中选择最小数来重新排列 public static void selectSort(int[] line) { for (int i = 0; i < line.length - 1; i++) { int min = i; // 每次从未排序数组中找到最小值的坐标 for (int j = i + 1; j < line.length; j++) { if (line[j] < line[min]) { min = j; } } // 将最小值放在最前面 if (min != i) { int temp = line[min]; line[min] = line[i]; line[i] = temp; } } System.out.println(Arrays.toString(line)); } }
分析:简单选择排序过程中需要进行的比较次数与初始状态下待排序的记录序列的排列情况** 无关。当i=1时,需进行n-1次比较;当i=2时,需进行n-2次比较;依次类推,共需要进行的比较次数是(n-1)+(n-2)+…+2+1=n(n-1)/2,即进行比较操作的时间复杂度为 O(n^2) ,进行移动操作的时间复杂度为 O(n) 。总的时间复杂度为 O(n^2) **。
简单选择排序是不稳定排序。
//插入排序 的伪代码 INSERTION-SORT(A) for j = 2 to A.length key = A[j] //insert A[j] into the sorted sequence A[1..j-1] i = j - 1 while i >= 0 and A[i] > key A[i+1] = A[i] i = i - 1 A[i+1] = key
实现
package cn.xdf.Algorithm; import java.util.Arrays; public class insertSort { public static void main(String[] args) { int[] arr = { 5, 2, 4, 6, 1, 3 }; // INSERTION-SORT(A) for (int j = 1; j < arr.length; j++) { // j=1,从第二位开始 int tmp = arr[j]; // tmp=2 int i = j - 1; // i=0 while (i >= 0 && arr[i] > tmp) { // 5 > 2 前一位和后一位比较 arr[i + 1] = arr[i]; // 把较大的数赋值给后一位 i = i - 1; // 为了跳出while循环 } arr[i + 1] = tmp; // 把较小的数赋值为前一位(也就是把小的插到前面) } System.out.println(Arrays.toString(arr)); // 升序-打印插入排序后的新数组 // 如果看不太懂的话,debug跑一遍就好了 } }
分析:最好情况下,当待排序序列中记录已经有序时,则需要n-1次比较,不需要移动,时间复杂度为 O(n) 。最差情况下,当待排序序列中所有记录正好逆序时,则比较次数和移动次数都达到最大值,时间复杂度为 O(n^2) 。平均情况下,时间复杂度为 O(n^2) 。
4.希尔排序
希尔排序又称“缩小增量排序”,它是基于直接插入排序的以下两点性质而提出的一种改进:
(1) 直接插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率。
(2) 直接插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位。
5.归并排序
归并排序是分治法的一个典型应用,它的主要思想是:将待排序序列分为两部分,对每部分递归地应用归并排序,在两部分都排好序后进行合并。
例如,排序序列(3,2,8,6,7,9,1,5)的过程是,先将序列分为两部分,(3,2,8,6)和(7,9,1,5),然后对两部分分别应用归并排序,第1部分(3,2,8,6),第2部分(7,9,1,5),对两个部分分别进行归并排序,第1部分继续分为(3,2)和(8,6),(3,2)继续分为(3)和(2),(8,6)继续分为(8)和(6),之后进行合并得到(2,3),(6,8),再合并得到(2,3,6,8),第2部分进行归并排序得到(1,5,7,9),最后合并两部分得到(1,2,3,5,6,7,8,9)。
package cn.xdf.Algorithm; import java.util.Arrays; public class mergeSort { public static void main(String[] args) { int[] arr = { 3, 2, 8, 6, 7, 9, 1, 5 }; funMergeSort(arr); System.out.println(Arrays.toString(arr)); //[1, 2, 3, 5, 6, 7, 8, 9] } public static void funMergeSort(int[] arr) { // 归并排序 if (arr.length > 1) { int length1 = arr.length / 2; int[] arr1 = new int[length1]; System.arraycopy(arr, 0, arr1, 0, length1); // [3,2,8,6] System.out.println(Arrays.toString(arr1)); funMergeSort(arr1); // 递归 int length2 = arr.length - length1; int[] arr2 = new int[length2]; System.arraycopy(arr, length1, arr2, 0, length2); // [7,9,1,5] System.out.println(Arrays.toString(arr2)); funMergeSort(arr2); // 递归 int[] arr3 = merg(arr1, arr2);// 自定义方法 System.arraycopy(arr3, 0, arr, 0, arr.length); System.out.println(Arrays.toString(arr3)); } } public static int[] merg(int[] arr1, int[] arr2) { int[] arr3 = new int[arr1.length + arr2.length]; int count1 = 0; int count2 = 0; int count3 = 0; while (count1 < arr1.length && count2 < arr2.length) { if (arr1[count1] < arr2[count2]) { arr3[count3++] = arr1[count1++]; } else { arr3[count3++] = arr2[count2++]; } } while (count1 < arr1.length) { arr3[count3++] = arr1[count1++]; } while (count2 < arr2.length) { arr3[count3++] = arr2[count2++]; } return arr3; } }
//控制台输出 [3, 2, 8, 6] [3, 2] [3] [2] //第一个分支拆分完 [2, 3] //调用自定义方法,合并两个分支并排序 [8, 6] [8] [6] [6, 8] [2, 3, 6, 8] //第一个大分支,合并并排序完 [7, 9, 1, 5] [7, 9] [7] [9] [7, 9] [1, 5] [1] [5] [1, 5] [1, 5, 7, 9] //第二个大分支,合并并排序完 [1, 2, 3, 5, 6, 7, 8, 9] [1, 2, 3, 5, 6, 7, 8, 9]
分析:归并排序的时间复杂度为O(nlogn),它是一种稳定的排序,java.util.Arrays类中的sort方法就是使用归并排序的变体来实现的。
6.快速排序
快速排序的主要思想是:在待排序的序列中选择一个称为主元的元素,将数组分为两部分,使得第一部分中的所有元素都小于或等于主元,而第二部分中的所有元素都大于主元,然后对两部分递归地应用快速排序算法。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号