DS博客作业06--图

1.本周学习总结

 1.1思维导图

 1.2谈谈你对图结构的认识及学习体会。

图这一章节算法很多，用到适当的算法可以是代码量及存储空间少很多，使得更加便利，例如用广度遍历时好比一棵树,访问初始顶点的所有没有被访问过的孩子,再从访问的孩子里访问它的所有没有被访问过的孩子，直至所有孩子都被访问过为止,使用队列会比较好

2.PTA实验作业

 2.1.题目7-1图着色问题

 2.1.1设计思路

建立邻接矩阵 
定义vis[MAXV]={0}标志颜色是否存在，0为不存在，1为存在
定义颜色种类num=0，flag表示方案正误，1为错误，0为正确； 
for i=1 to g.v
    输入颜色种类；
    if 该颜色不存在{
        颜色种类num++；
        标记该颜色存在 
    } 
end for
if 颜色种类不为k种，flag=1； 
遍历每个顶点
    if 两个顶点相邻并且颜色相同
        flag=1；退出循环
if flag为1   输出NO
else  输出Yes 

 2.1.2代码截图

 2.1.3本题PTA提交列表说明

• 这当中的问题存在
  顶点遍历错误
  

 2.2 题目2 7-3六度空间

 2.2.1设计思路

首先要确认的是用 DFS还是BFS，考虑到你要找的人，可能是你朋友的朋友的朋友。。每个人都有自己的交际圈，所以把每个人（结点）的交际圈看成一层，那么只要不超过六层的结点就是符合要求的，因此应用BFS。

 2.2.2代码截图

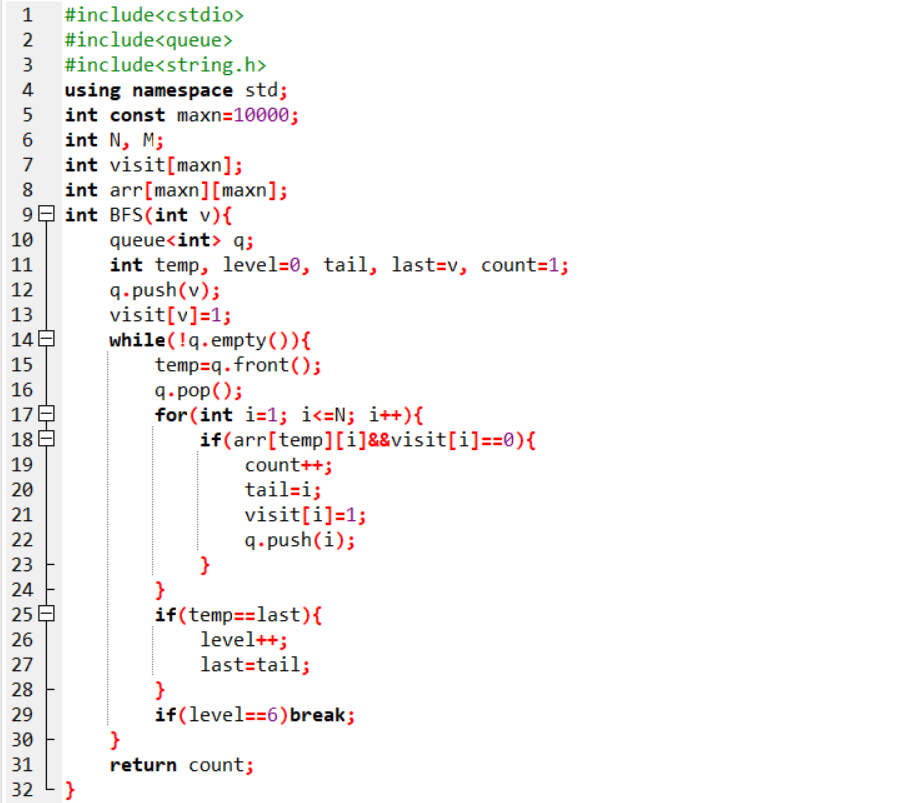
 2.2.3本题PTA提交列表说明。

题中两个正整数，分别表示社交网络图的结点数N（1<N≤104，表示人数）、边数M（≤33×N，表示社交关系数）
所以用数组时二维数组开的太大了。

 2.3 题目3 7-4公路村村通

 2.3.1设计思路

定义数组a[][]记录边的权值关系，初始值为inf;
定义变量min表示每条道路最低预算;变量sum表示最低成本 
    for i=1 to n
        dis[i]=a[1][i]; 
    end for 
    for i=2 to n{ 
       min置为inf;
    for j=1 to n
        if (顶点未被访问且该边权值小于min) {
            最低预算min置为该边权值;
            记录最近顶点的编号flag； 
        }
            sum累加最低成本 
            flag顶点标记已访问 
            for j=1 to n
                修改数组dis}
    end for
   if(sum值越界即表示不连通）输出-1；
   else 输出 sum的值；

 2.3.2代码截图

 2.3.3本题PTA提交列表说明。

一直有个点没有过去，后来经过不断尝试发现时判断村是否全部连通的问题，在询问同学后成功解决。

3、上机考试错题及处理办法

 3.1.截图错题代码

一、7-1六度空间

 3.2 错的原因及处理方法

错误：

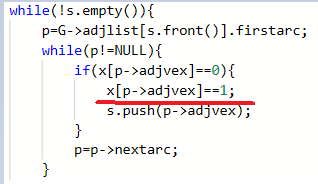
正确：

图中x[p->adjvex] = 1;写成了x[p->adjvex] ==1;
真的就是一个“=”毁所有，太致命了。呜呜

二、7-2公路村村通

• 这次的题代码量有点多，到最后实在写不完了，前面7-1六度空间一直卡在那太久，一直过不去心态有点炸了。就写不下去了。