过河卒

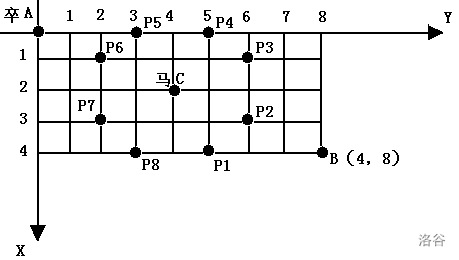
设s为该点在地图上的状态。注意坐标都+2防止数组越界了。

因为卒行走的规则是可以向下、或者向右的。所以得出状态转移方程为 \(f(i, j) = f(i-1,j)+f(i,j-1)\)

第一次做 \(DP\) 题啊，还是有一些不懂的。

具体上 \(Code\)

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int fx[] = {0, -2, -1, 1, 2, 2, 1, -1, -2}; // fx与fy对应位马可以走到的位置坐标
const int fy[] = {0, 1, 2, 2, 1, -1, -2, -2, -1};
int bx, by, mx, my; // (bx,by)是目标位置 (mx,my)是马的位置
ll f[40][40];
bool s[40][40]; // 判断点的状态（是否被拦住）
int main()
{
    cin >> bx >> by >> mx >> my;
    bx += 2, by += 2, my += 2, mx += 2; // 全部+2防止越界
    f[2][1] = 1; // f[1][2]也可以，防止0+0没有意义
    s[mx][my] = 1;
    for (int i = 1; i <= 8; i++)
        s[mx + fx[i]][my + fy[i]] = 1; // 标记马可以走到的绝对坐标 8个
    for (int i = 2; i <= bx; i++)
        for (int j = 2; j <= by; j++)
        {
            if (s[i][j])
                continue; // 被拦住直接跳过
            f[i][j] = f[i - 1][j] + f[i][j - 1];
        }
    cout << f[bx][by];
    return 0;
}

重要的一点就是怎么巧妙的把马可以走到的相对位置转为绝对位置，见主函数的第一个 \(for\) 循环。