光展守恒定律

---

[Illumination Engineering Design with Nonimaging Optics (R. John Koshel (Editor)) (Z-Library).pdf]

1 问题

是否有可能用光学器件先把太阳光的张角减小也就是光展角减小，然后再聚光。我们能否理论上证明这一点？光转角减小之后向远处传输它的光斑就可能减小。很多面这样的镜子往一个地方去，虽然受到1万倍的这个聚光比限制，到达远处的光斑也可能不会很大。其实我们工程上只要1000多倍就很厉害了。

---

2 回答

从理论上说光展角守恒，光展角无法减小。但可以不断改变相对平面，使得光斑聚焦

光展守恒的三种证明方法，

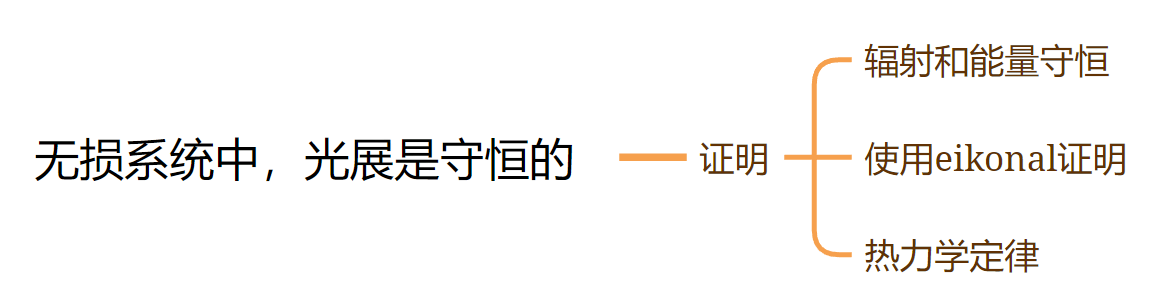
还可以使用刘维尔定理和应用于哈密顿系统的斯托克斯定理

---

1.1 SQUEEZING THE ÉTENDUE

---

• étendue squeezing
• étendue remapping

由这两种方法设计一起，能够解用平面对称光学解决不了的问题

Étendue Rotating Mappings

\[\begin{align} x' &= y + \sigma p \\ y' &= x + \sigma q \\ p' &= q \\ q' &= p \end{align} \]

Étendue Squeezing Mappings（2:1压缩）

\[x' = \begin{cases} 2x - x_0 + \sigma p \\ 2x + x_0 + \sigma p \end{cases} \]

\[y' = \begin{cases} \frac{1}{2}y + \frac{1}{2}y_0 + \sigma q \\ \frac{1}{2}y - \frac{1}{2}y_0 + \sigma q \end{cases} \]

\[p' = \frac{p}{2} \]

\[q' = 2q \]

---

1.1.1 etendue squeezer（透镜）

---

• 实现可变压缩光学的一种方法是将光学系统划分为两个或多个透镜对。每一对透镜将拦截来自光源的部分光通量，然后将其转移到目标。每个透镜对产生的角扩散或压缩将由透镜对的镶嵌决定。（这里2:1的意思是——使照片上的图像在一个维度上拉伸两倍，在另一个维度上压缩相同的）

图3.6 使用两个透镜元件对的2:1模数压缩光学元件。（水平延展压缩了）

图3.7 使用三个透镜元件对的光展压缩光学。（垂直平面有更高的对称性）

图3.8 使用五个透镜元件对的光展压缩光学。（水平平面有更高的对称性）

1.1.1 主要聚焦的四种方式

1.1.2 聚光镜-反射镜

传统的椭圆聚光镜

二级聚光——先收集光，在集中发射

2 using light guiding manifold（light guiding manifold）

例如U.S. Patent 7,520,641所述，这些设计的基石是light shifters 。这些“移动”光的同时保持其面积和角孔径。
图3.31a展示了其中一种装置的例子。每一面都由一面平镜和一条抛物线弧组成。它将光线横向移动距离s，同时保持其面积d和角孔径θ。在这个简单的装置中，沿着抛物线移动光圈的边缘P，就可以调节横向位移，如图3.31b所示。

再举一个例子，考虑这样一个情况，如图3.32a所示，我们想要将一个宽高比为2 ×2的光源转换到另一个宽高比为1 ×4的光源上。其中一个器件由两个独立的部分组成，每个部分由两个移光器组成。它将方形光源分成两半(1 ×2宽高比)，然后将它们并排放置。

图3.32b显示了另一个改变光源宽高比的设备示例。它从3 ×3宽高比变为1 ×9。光学元件由三部分组成。其中两个由两个移光器组成，中间的一个是直光波导。

---

附录

目前聚焦系统的根基：伽利略聚焦系统、开普勒聚焦系统

伽利略聚焦系统

开普勒聚焦系统

汇聚比的计算

\[C_3D=\frac{A}{A'}=(\frac{n'\sin\theta '}{n'\sin\theta })^2 \]