数据结构-图-最小生成树
最小生成树表示得是连通图的极小连通子图,它包含所有的的顶点,但足以生成n-1条边的数。
下面是我学习的内容和理解。
1.使用普里姆算法构成最小生成树。
先讲一下普里姆算法的思路。普里姆算法思路是这样的:
前提:G={V,E} 这个是我们图的定义这个应该是明白啥意思的。
1.现在定义一个V1表示一个空的新集合
2.首先随机的将V中的一个节点放入到V1中,作为遍历图开始位置
3.其次选取V1中的一个节点和选取V中的一个节点,使边的权值是E中最小的(必须是存在E中的,不然不是两个节点不是连通的,也没用意义。第一次从V1只能选取我们随机取的那个节点啦,但是后面需要看情况)
4.再将V中的那个节点放入到V1中来,并且将我们刚才在第三3步使用过的那边条从E中删除,重复第3步,只到V1=V.
下面是JAVA实现:
private int edgeSize; private int vertexeSize; public static final int MAX_VALUE = Integer.MAX_VALUE; private List<Edge> minimumTreeEdges = new ArrayList<>(); //最小生成树 n-1 private int[][] arc = new int[9][9]; //边集合 邻接矩阵表示方式 /** * 普里姆构建最小生成树 */ public void buildMinimumTreeByPrim() { int[] minimumLine = new int[vertexeSize]; int[] minimumLine2LastSearched = new int[vertexeSize]; //这里是记录上一次最小权值节点的下标 for (int i = 1; i < vertexeSize; i++) { minimumLine[i] = arc[0][i]; //首先将第一排的数据作为最小的一列值后面将从这其中查找最小权值 minimumLine2LastSearched[i] = 0; } minimumLine[0] = 0; //0已经在加入到了遍历过的节点中去 minimumLine2LastSearched[0] = 0;//表示0是0的上一次的最小权值(因为0是开始,所以前面还是0了) for (int i = 1; i < vertexeSize; i++) { int k = 0, min = MAX_VALUE; for (int j = 1; j < vertexeSize; j++) { if (minimumLine[j] != 0 && minimumLine[j] < min) { //这里是找目前所有的边中权值最小的那个 min = minimumLine[j]; k = j; } } // NotBoundEdge edge = new NotBoundEdge(minimumLine2LastSearched[k], k); //如果是第一次的话 为0 因为由0这个最小权值计算出了k这个最小权值 // minimumTreeEdges.add(edge); System.out.println("("+minimumLine2LastSearched[k]+","+k+")"); minimumLine[k] = 0; //因为这个k已经遍历过了 所以设置为0 for (int j = 0; j < vertexeSize; j++) { if (minimumLine[j] != 0 && arc[k][j] < minimumLine[j]) { minimumLine[j] = arc[k][j]; //如果有比其他更小权值得节点 那么就覆盖(更大的权值已经没有任何意义了) minimumLine2LastSearched[j] = k; //这里就表示k是j的上一个节点(如果权值最小 也就是: (k,j)) } } } }
上面不是我自己实现的,上面的思路是网上最为流行的,所以就将这种算法理解了一下(把变量名改了一下,以前的i,j,k真是不能忍),然后加了一些自己的理解.我觉得这个算法很不好理解的地方在于
int[] minimumLine = new int[vertexeSize];
int[] minimumLine2LastSearched = new int[vertexeSize]; //这里是记录上一次最小权值节点的下标
这两个数组,因为的代码基本都没怎么讲明白(可能刚好我看的几遍都没讲清楚),所以我就加上自己的注释了,linimumLine 一开始记录的和0相关的权值,但是到了后来就不是了,是记录了每一行只要比它对应的那一列小的权值.
2 克鲁斯卡尔算法
这个算法的原理是这样的:
前提:G={V,E}
1.先定义 一个T={V1,{}},初始化的时候,T中是没有边的,只有n个顶点,图中的每一个节点都作为一个连通分量
2.在E中选择代价最小的边,若边依附于不用的连通分量,那么就将这个边放到T中,否则就丢弃这条边,一直到T中的所有的几点都在一个连通分量上
代码:
private NetNode[] netNodes=new NetNode[15];
/** * TODO * 根据克鲁斯卡尔构建最小生成树 */ public void buildMinimumByKruskal() { int[] parent=new int[edgeSize]; for (int i=0;i<vertexeSize;i++){ parent[i]=0; } int m,n; for (int i=0;i<vertexeSize;i++){ /** * 如果这里求出的n=m的话 那么就表示构成环了( * 因为parent[index]>0的话 就会接着往下走,直到parent[index]=0. * 这条路线可以看成是边连在一起的. * 这里就相当于从begin 和end 这两个点开始往下一直连线[直到parent[index]=0结束]. * 如果碰到了一块(m=n) 那么就说明他们相遇了 * ) */ m=findNode(parent,netNodes[i].getBegin()); n=findNode(parent,netNodes[i].getEnd()); if(m!=n){ parent[n]=m; System.out.println("("+netNodes[i].begin+","+netNodes[i].getEnd()+")"); } } } /** * 这里比较难理解 * 1.这里其实就是想查看是否在用一个子集(如果parent[index]=0 * 那就也就表示没有连在一起) * @param parent * @param index * @return */ public int findNode(int[] parent, int index) { while (parent[index] > 0) { index = parent[index]; } return index; } public interface Edge { int getBegin(); int getEnd(); int getWeight(); } /** * */ public class NetNode implements Edge { private int begin; private int end; private int weight; public int getBegin() { return begin; } public void setBegin(int begin) { this.begin = begin; } public int getEnd() { return end; } public void setEnd(int end) { this.end = end; } public int getWeight() { return weight; } public void setWeight(int weight) { this.weight = weight; } }
注意我这里没体现出的一个地方是:放进去的netNodes是按照权值从小到大的:
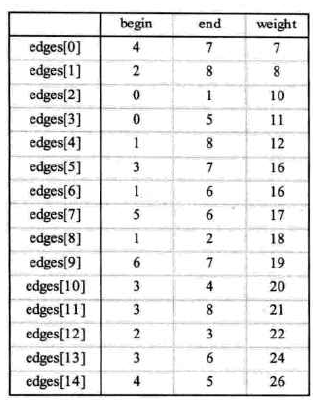
参考:
大话数据结构 第七章




