3_确定性推理
推理概述
推理的基本概念
推理就是按照某种策略从已有事实和知识推出结论的过程
推理的分类
| 分类方式 | 类别1 | 类别2 |
|---|---|---|
| 逻辑基础 | 演绎推理 | 归纳推理 |
| 所用知识的确定性 | 确定性推理 | 不确定性推理 |
| 推理策略是否使用启发式知识 | 启发式推理 | 非启发式推理 |
详谈逻辑推理分类
| 推理方式 | 概念 | 常用形式 | 特点 |
|---|---|---|---|
| 演绎推理 | 一般到个别 | 三段论法(大前提、小前提、结论) | 不能增殖新知识 |
| 归纳推理 | 个别到一般 | 完全归纳推理,不完全归纳推理 | 可以增殖新知识 |
产生式系统的推理
可以分为以下类别:正向推理,逆向推理,双向推理
| 推理形式 | 优点 | 缺点 |
|---|---|---|
| 正向推理 | 较为直观 | 推理无明确的目标,求解问题时可能会执行许多与解无关的操作,导致推理效率较低 |
| 逆向推理 | 不必寻找和使用那些与假设目标无关的信息和规则,推理过程的目标明确 | 当用户对解的情况认识不清时,由系统自主选择假设目标的盲目性比较大,若选择不好,会影响系统效率。 |
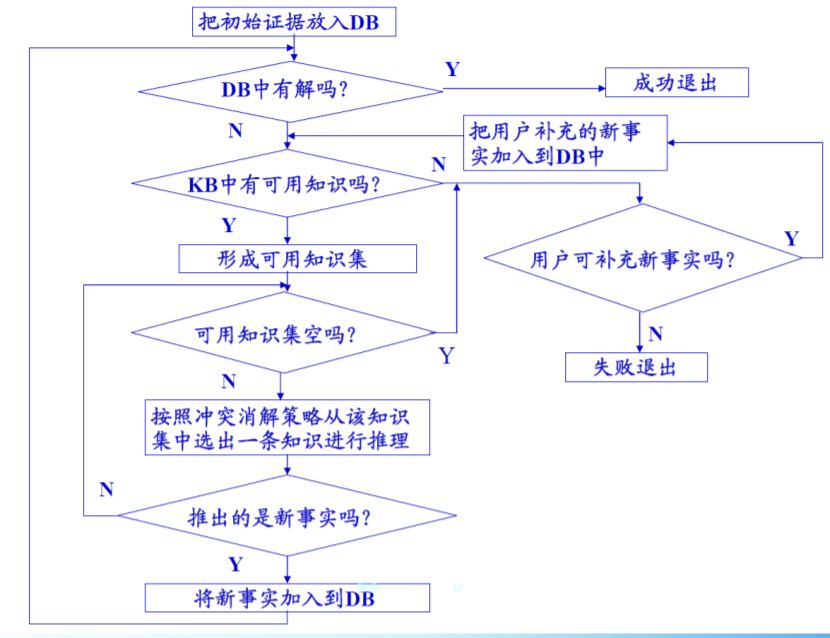
正向推理
- 把用户提供的初始证据放入综合数据库。
- 检查综合数据库中是否包含了问题的解,若已包含,则求解结束,并成功推出;否则执行下一步。
- 检查知识库中是否有可用知识,若有,形成当前可用知识集,执行下一步; 否则转(5)。
- 按照某种冲突消解策略,从当前可用知识集中选出一条规则进行推理,并将 推出的新事实加入综合数据库种,然后转(2)。
- 询问用户是否可以进一步补充新的事实,若可补充,则将补充的新事实加入 综合数据库中,然后转(3);否则表示无解,失败退出。
逆向推理
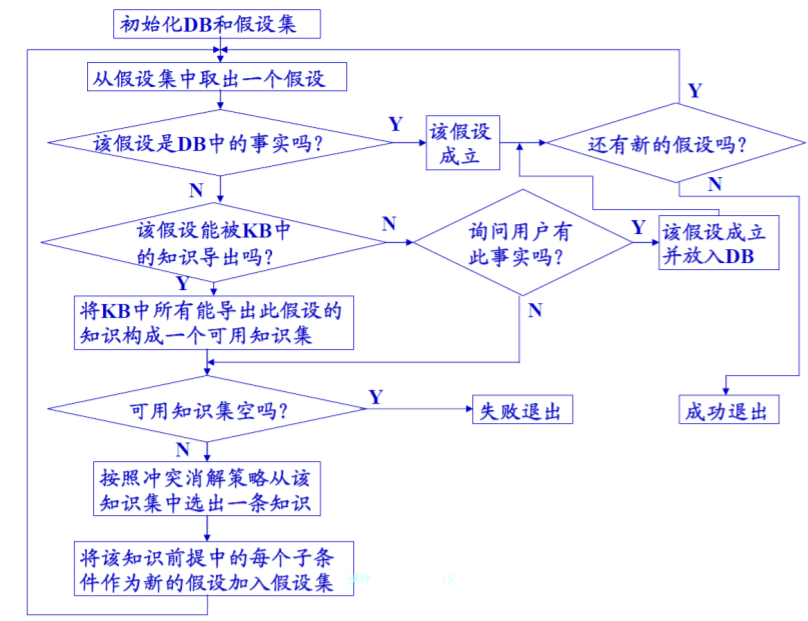
- 将要求证的目标(称为假设)构成一个假设集。
- 从假设集中选出一个假设,检查该假设是否在综合数据库中。
- 若不在,则执行第3步。
- 若在, 则该假设成立,删除假设集中成立的假设,重复执行第2步。
- 此时,若假设集为空,则成功退出,否则仍执行。
- 检查该假设是否可由知识库的某个知识导出,将知识库中可以导出该假设的所有知识构成一个可用知识集。
- 检查可用知识集是否为空,若是,失败退出;否则执行下一步。
- 按冲突消解策略从可用知识集中取出一个知识。将该知识的前提中的每个子条件都作为新的假设放入假设集,删除原假设,然后转(2)。
双向推理
结合版,可以先正向后逆向,也可以先逆向后正向
例子
假设知识库中包含有以下2条规则:
r1 :IF B THEN C
r2 :IF A THEN B
已知初始证据A,求证目标C。
正向推理求解
- 推理开始前,综合数据库为空。
- 推理开始后,先把A放入综合数据库,然后检查综合数据库中是否含有该问题的解,回答为“N”。
- 接着检查知识库中是否有可用知识,显然r2可用,形成仅含r2 的知识集。从该知识集中取出r2 ,推出新的实事B,将B加入综合数据库。
- 检查综合数据库中是否含有目标C, 回答为“N”。
- 再检查知识库中是否有可用知识,此时由于B的加入使得r1为可用,形成仅含r1的知识集。从该知识集中取出r1 ,推出新的事实C,将C加入综合数据库,检查综合数据库中是否含有目标C,回答为“Y”。
- 它说明综合数据库中已经含有问题的解,推理成功结束,目标C得证。
逆向推理求解
- 推理开始前,综合数据库和假设集均为空。
- 推理开始后,先将初始证据A和目标C分别放入综合数据库和假设集,然后从假设集中取出一 个假设C,查找C是否为综合数据库中的已知事实,回答为“N”。
- 再检查C是否能被知识库中的知识所导出,发现C可由r1 导出,于是r1 被放入可用知识集。由于知识库中只有r1 可用,故可用知识集中仅含r1 。 接着从可用知识集中取出r1 ,将其前提条件B作为新的假设放入假设集。
- 从假设集中取出B,检查B是否为综合数据库中的实事,回答为“N”。
- 再检查B是否能被知识库中 的知识所导出,发现B可由r2 导出,于是r2被放入可用知识集。由于知识库中只有r2可 用,故可用知识集中仅含r2 。 从可用知识集中取出r2 ,将其前提条件A作为新的假设放入假设集。
- 然后从假设集中取出A,检查A是否为综合数据库中的实事,回答为“Y”。
- 它说明该假设成立,由于无新的假设,故推理过程成功结束,于是目标C得证。
一阶谓词逻辑基础
谓词公式的解释
定义,设D是谓词公式P的非空个体域,若对P中的常量,函数和谓词按如下规定赋值:
- 为每个个体常量指派D中的一个元素;
- 为每个n元函数指派一个从Dn到D的一个映射,其中 Dn = {(x1,x1,...,xn)|x1,x1,...,xn ∈ D}
- 为每个n元谓词指派一个从Dn到{F,T}的映射
则称这些指派为P在D上的一个解释。
- 可以确定在一个指派下,某个谓词公式的真或假。
例子,谓词公式在解释下的真值确定


全称固化
y是个体域中的任一个体,依此可消去谓词公式中的全称量词。
存在固化
y是个体域中某一个可以使P(y)为真的个体,依此可消去谓词公式中的存在量词。
置换与合一
置换与合一的目的:将相同谓词名但个体不同的情况做出处理,使得二者变量名相同
- 差异集:在对两个谓词公式中的项从左到右进行比较时,那些第一个不 相同的项所构成的集合,称为差异集。
合一,设有公式集F={F1 , F2 ,…,Fn },若存在一个置换θ,可使 F1θ=F2θ=…=Fnθ, 则称θ是F的一个合一。称F1 ,F2 ,…,Fn是可合一的。否则,是不可合一的。
最一般合一的求取算法
-
置k=0, 谓词公式集Sk=S,置换集σk=ε
-
若Sk只含有一个谓词公式,则算法停止,σk就是要求的最一般合一
-
求Sk的差异集Dk
-
若Dk中存在元素xk和tk,其中xk是变元,tk是项且xk不在tk中出现,则置Sk+1= Sk · {tk /xk}, σk+1=σk · {tk / xk},k=k+1,然后转②
-
算法停止,S的最一般合一不存在。
以本人看来,就是寻找差异集作为置换,使用常元替换变元,使用函词替换简单个体元
例子


自然演绎推理
概念
思想
从一组已知为真的事实出发,直接运用命题 逻辑或谓词逻辑中的推理规则推出结论的过程
推理基础:
| 名称 | 逻辑表示 |
|---|---|
| 假言三段论 | 𝑃 → 𝑄,𝑄 → 𝑅 ⇒ 𝑃 → R |
| 假言推理 | 𝑃, 𝑃 → 𝑄 ⇒ 𝑄 |
| 拒取式推理 | 𝑃 → 𝑄,¬Q ⇒ ¬P |
例子,纯粹的逻辑应用
已知,下列公式为真
\[R, S, R→T, S∧T →P, P →Q \]求证,Q为真
例子,合一+推理
已知,下列公式为真
\[W (a),(∀x)(W (x) → Q(x)) \]求证,Q(a)为真

例子,实用例子
设已知如下事实
- 如果是需要编程序的课,王程都喜欢。
- 所有的程序设计语言课都是需要编程序的课。
- C是一门程序设计语言课。
求证:王程喜欢C这门课。

归结演绎推理
概念
思想
采用反证法的思想, 把关于永真性的证明转化为关于不可满足性的证明,要证明P→Q永真,只要能够证明P∧﹁Q是不可满足的即可。
子句集化简方法
-
消去连接词
→和↔,反复使用如下等价公式P→Q ⇔﹁P∨Q&&P↔Q ⇔(P∧Q)∨(﹁P∧﹁Q) -
减少否定符号的辖域,使用
﹁(∀x)P(x)⇔(∃x)﹁P(x)&&﹁(∃x)P(x)⇔(∀x)﹁P(x) -
不同量词约束的变元有不同的名字。
-
化为前束范式,把所有量词都移到公式的左边,并且在移动时不能 改变其相对顺序。
-
消去存在量词。
- 若存在量词不出现在全称量词的辖域内(即它的左边没有全称量词),只要用一个新的个体常量替换受该存在量词约束的变元,就可消去该存在量词。
- 若存在量词位于一个或多个全称量词的辖域内,则需要该全称量词的函词替换受该存在量词约束的变元y,然后再消去该存在量词。(值得注意的是,是否在某个全程量词的辖域,请看化为前束范式之前的等式,且必须是在辖域内,如果是两个共享一个辖域可以交换,不做处理)
-
展开为标准合取式。
-
消去全称量词。直接去掉就可以。
-
消去合取词,并更换变量名称,得到子句集。
归结
命题逻辑的归结
设C1 和C2是子句集中的任意两个子句,if C1中的文字L1与C2中的文字L2互补,then可从C1 和C2 中分别消去L1 和L2 ,并将C1 和C2 中余下的部分按析取关系构 成一个新的子句C12 ,则C12为C1和C2的二元归结式。
谓词逻辑的归结
设C1和C2是两个没有公共变元的子句,L1和L2分别是C1和C2中的文字。if L1和¬L2存在一个最一般合一σ,then 称 C12 =({C1σ}-{ L1σ})∪({ C2σ}-{ L2σ}) 为C1和C2的二元归结式。
- 归结前,消去每个归结式中可以合一的文字
- 换元消去两个归结式中相同的元素
- 一次归结只能消去一个变元
归结演绎推理总问题
已知 F,求证G
- 否定目标公式G,得﹁G
- 把﹁G并入到公式集F中,得到
- 把{F,﹁G}化为子句集S。
- 应用归结原理对子句集S中的子句进行归结,并把每次得到的归结式并入S中(并入S中,不代表删除归结的原子句)。如此反复进行,若出现空子句,则停止归结,此时就证明了G为真。
求解问题
- 把已知条件用谓词公式表示,并化成相应的子句集S1
- 把待求解的问题也用谓词公式表示,然后将其否定,并与谓词ANSWER构成析取式G1;
- 把G1化为子句集S2,并把子句集S2与S1合并构成新子句集S
- 对子句集S应用谓词归结原理进行归结,在归结过程中通过合一置换, 改变ANSWER中的变元
- 如果得到归结式ANSWER,则问题的答案就在ANSWER谓词中
归结策略
归结策略的目的:每一步选取何时的归结子句,以尽快得到空子句
| 有用的归结策略 | 阐述 |
|---|---|
| 纯文字删除法 | 删除子句集中包含纯文字的子句 |
| 重言式删除法 | 删除子句集中包含重言式的子句 |
| 包孕删除法 | 删除子句集中被包孕的子句 |
| 支持集策略 | 被归结的子句必须有目标子句或者其后裔 |
| 没用的,看看就可的归结策略 | 阐述 |
|---|---|
| 排序策略 | 每一步都尽可能地计算子句 |
| 线形输入策略 | 被归结的子句必须有原子句集的子句 |
| 单文字子句策略 | 被归结的子句必须有单文字子句 |
纯文字删除法
- 纯文字:如果某文字L在子句集中不存在可与其互补的文字﹁L,则称该文字为纯文字。
- 删除子句集中包含纯文字的子句
例子
\[S=\{ P∨Q∨R, ﹁Q∨R, Q, ﹁R \} \]
P是纯文字,因此可以将子句P∨Q∨R从子句集S中删除
重言式删除法
- 重言式:如果一个子句中包含有互补的文字对,则称其为重言式。
- 删除子句集中包含重言式的子句
例子
\[P(x)∨﹁P(x), P(x)∨Q(x)∨﹁P(x) \]
全部可以删除
包孕删除法
- 包孕:设有子句C1 和C2 ,如果存在一个置换σ,使得C1σ ⊆ C2 ,则称C1包孕于C2。
- 删除子句集中被包孕的子句
\[\begin{align} & P(x) & 包孕于 & \quad P(a) & σ=\{a/x\}\\ & P(x) & 包孕于 & \quad P(a)∨Q(z) & σ=\{a/x\}\\ & P(x)∨Q(a) & 包孕于 & \quad P(f(a))∨Q(a)∨R(y) & σ=\{f(a)/x\}\\ & P(x)∨Q(y) & 包孕于& \quad P(a)∨Q(u)∨R(w) & σ=\{a/x, u/y\} \\ \end{align} \]
全部可以删除左边的部分
支持集策略
- 要求每一次参加归结的两个亲本子句中,至少应该有一个是由目标公式的否定所得到的子句或它们的后裔。
特点
- 完备,缩减了子句集的归结,增加了子句集归结的深度
例子
\[S=\{﹁I(x)∨R(x), I(a),﹁R(y)∨L(y), ﹁L(a) \} \]其中﹁I(x)∨R(x)为目标公式的否定。
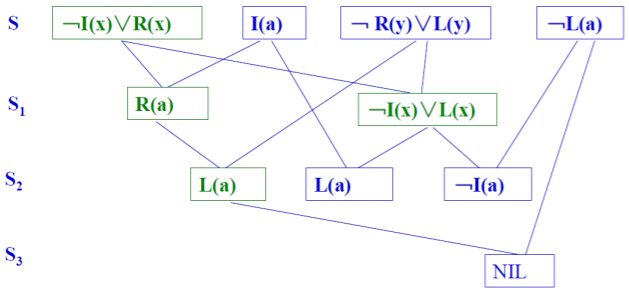
排序策略(广度度优先策略)
过程:
-
从S0出发,对S0中的全部子句作所有可能的归结,得到第一层归结式,把这些归结式的集合记为S1
-
用S0中的子句与S1中的子句进行所有可能的归结,得到第二层归结式,把这些归结式的集合记为S2
-
用S0和S1中的子句与S2中的子句进行所有可能的归结,得到第三层归结式,把这些归结式的集合记为S3。
-
如此继续,知道得出空子句或不能再继续归结为止
特点
- 完备,可以找到最短归结路径
- 归结效率较低,可能出现组合爆炸
例子
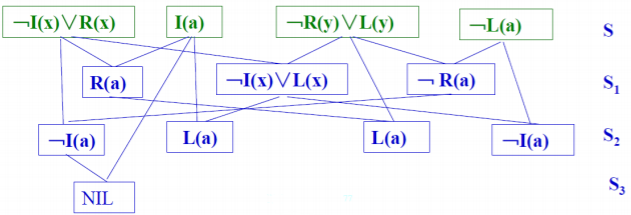
\[S=\{﹁I(x)∨R(x), I(a), ﹁R(y)∨L(y), ﹁L(a) \} \]
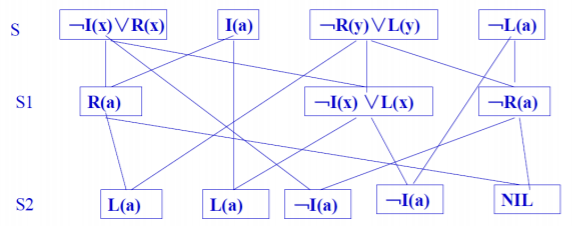
线形输入策略
- 要求每次参加归结的两个亲本子句中,至少应该有一个是初始子句集中的子句。
- 所谓初始子句集是指开始归结时所使用的子句集。
特点
- 不完备,可能高效
例子
\[S=\{﹁I(x)∨R(x), I(a), ﹁R(y)∨L(y), ﹁L(a) \} \]
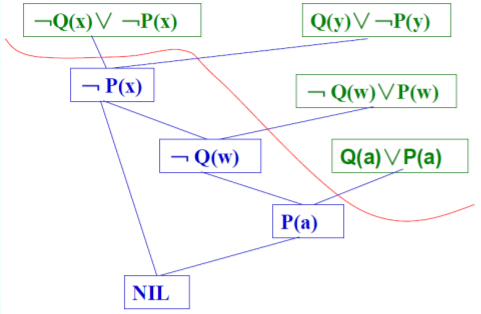
祖先过滤策略
每次参加归结的两个亲本子句,只要满足以下两个条件中的任意一个就可进行归结
- 两个亲本子句中至少有一个是初始子句集中的子句。
- 如果两个亲本子句都不是初始子句集中的子句,则一个子句应该是另一个 子句的先辈子句。
特点:完备的
例子
\[S=\{﹁Q(x)∨﹁P(x), Q(y)∨﹁P(y),﹁Q(w)∨P(w) , Q(a)∨P(a) \} \]
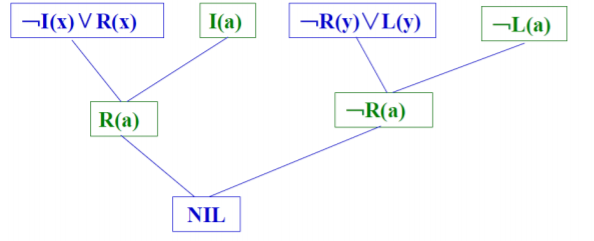
单文字子句策略
- 单文字:如果一个子句只包含一个文字,则称此子句为单文字子句
- 要求每次参加归结的两个亲本子句中至少有一个子句是单文字子句
特点
- 不完备的,效率较高
例子
\[S={﹁I(x)∨R(x), I(a), ﹁R(y)∨L(y), ﹁L(a) } \]
例子:化简子句集
\[(∀x)((∀y)P(x,y)→﹁(∀y)(Q(x,y)→R(x,y))) \]
- 消去连接词
→和↔
- 减少否定符号的辖域
- 不同量词约束的变元有不同的名字。
- 化为前束范式
- 消去存在量词。
- 展开为标准合取式。
- 消去全称量词。
- 消去合取词,并更换变量名称,得到子句集。
例子:归结(比较重要)
设:C1 =P(a)∨R(x),C2 =﹁P(y)∨Q(b),求C12
- 取L1 = P(a), L2 =﹁P(y),则L1 和﹁L2 的合一是σ=
设:C1 =P(x)∨Q(a),C2 =﹁P(b)∨R(x) ,求C12
- 先换元,令C2 =﹁P(b)∨R(y)
- 取L1 = P(x), L2 =﹁P(b),L1 和﹁L2 的合一是σ={b/x}。
设:C1 =P(x)∨﹁Q(b),C2 =﹁P(a)∨Q(y)∨R(z)
-
这道题需要注意的是,C1和C2的一次归结只能消去一个互补对,不能同时消去两个互补对
-
如在 σ={a/x, b/y}下,若同时消去两个互补对所得R(z)不是C1 和C2 的二元归结式
-
可以从另一个角度说明这道题的正确性:﹁P∨Q与P∨﹁Q永真,但是如果使用同时归结,那么可归结为NIL,是不可满足的,产生矛盾。
设:C1 =P(x)∨P(f(a))∨Q(x) ,C2 =﹁P(y)∨R(b),求C12
-
对参加归结的某个子句,若其内部有可合一的文字,则在进行归结之前应先进行合一。
-
严格来讲C1经过合一之后所得式子将不是C1,但是仍然认为该式与C2的二元归结式等同于C1和C2的二元归结式。也就是说,子句集合一之不影响原归结结果。
设C1 =P(y)∨P(f(x))∨Q(g(x)) ,C2 =﹁P(f(g(a)))∨Q(b),求C12
- 对C1 ,取合一σ={f(x)/y},得C1 的因子 C1 σ=P(f(x))∨Q(g(x))
- 对C1 的因子和C2 归结(σ={g(a)/x }),可得到C1 和C2的二元归结式 C12 =Q(g(g(a)))∨Q(b)
例子,使用归结演绎证明问题
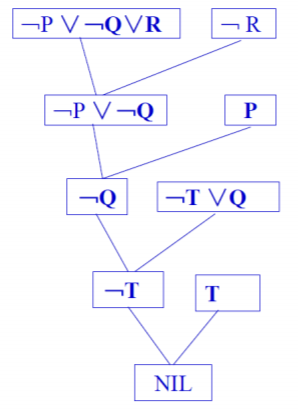
设已知的公式集为{P, (P∧Q)→R, (S∨T)→Q, T},求证结论R
假设结论R为假, 将﹁R加入公式集, 并化为子句集
归结如下图:
已知
\[F: (∀x)((∃y)(A(x, y)∧B(y))→(∃y)(C(y)∧D(x, y)))\\ G: ﹁(∃x)C(x)→(∀x)(∀y)(A(x, y)→﹁B(y)) \]求证G 是 F 的逻辑结论。
子句集为
归结过程如下
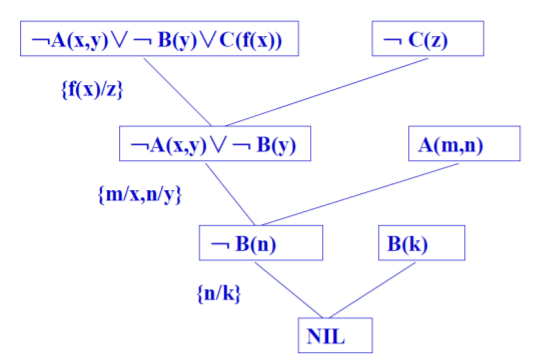
“激动人心的生活”问题
假设:
- 所有不贫穷并且聪明的人都是快乐的
- 那些看书的人是聪明的
- 李明能看书且不贫穷
- 快乐的人过着激动人心的生活。
求证:
- 李明过着激动人心的生活。
问题用谓词表示如下:
| 知识 | 知识表示 |
|---|---|
| 所有不贫穷并且聪明的人都是快乐的 | (∀x)((﹁Poor(x)∧Smart(x))→Happy(x)) |
| 那些看书的人是聪明的 | (∀y) (Read(y) →Smart(y)) |
| 李明能看书且不贫穷 | Read(Liming)∧﹁Poor(Liming) |
| 快乐的人过着激动人心的生活。 | (∀z) (Happy(z)→Exciting(z)) |
| 目标的否定:李明过着激动人心的生活 | ﹁Exciting(Liming) |
子句集
子句集的归结
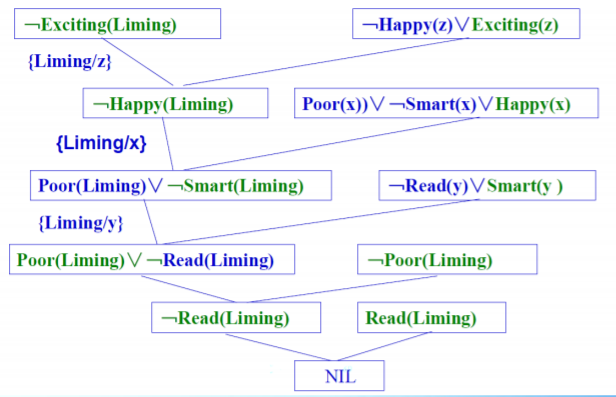
“快乐学生”问题
假设:
- 任何通过计算机考试并获奖的人都是快乐的
- 任何肯学习或幸运的人都可以通过所有考试
- 张不肯学习但他是幸运的
- 任何幸运的人都能获奖。
求证:张是快乐的。
问题用谓词表示如下
| 知识 | 知识表示 |
|---|---|
| 任何通过计算机考试并获奖的人都是快乐的 | (∀x)(Pass(x, computer)∧Win(x, prize)→Happy(x)) |
| 任何肯学习或幸运的人都可以通过所有考试 | (∀x) (∀y) (Study(x)∨Lucky(x)→Pass(x, y)) |
| 张不肯学习但他是幸运的 | ﹁Study(zhang)∧Lucky(zhang) |
| 任何幸运的人都能获奖 | (∀x) (Lucky(x)→Win(x, prize)) |
| 目标的否定:张是快乐的 | ﹁Happy(zhang) |
子句集
子句集的归结
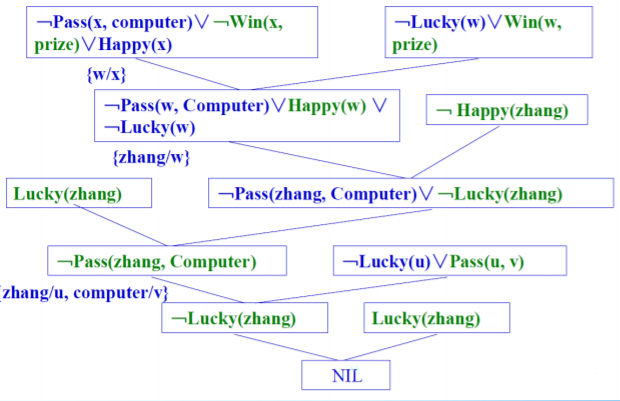
例子,使用归结演绎求解问题
已知:
- 如果x和y是同班同学,则x的老师也是y的老师。
- 王先生是小李的老师。
- 小李和小张是同班同学。
问:小张的老师是谁?
知识表示
| 知识 | 知识表示 |
|---|---|
| 如果x和y是同班同学,则x的老师也是y的老师 | (∀x)(∀y)(∀z)(C(x,y)∧T(z,x)→T(z,y) |
| 王先生是小李的老师 | T(Wang,Li) |
| 小李和小张是同班同学 | C(Li,Zhang) |
| 问题的表示 | ﹁ T(u,Zhang)∨ANSWER(u) |
化为子句集
归结
最终
- u=Wang,即小张的老师是王先生。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号