Longest palindrome subsequence

问题

来自于《Introduction to algorithm》(CLRS) Problem 15-2

A palindrome is a nonempty string over some alphabet that reads the same forward and backward. Examples of palindromes are all strings of length 1, civic, racecar,and aibohphobia (fear of palindromes). Give an efficient algorithm to find the longest palindrome that is a subsequence of a given input string. For example, given the input character, your algorithm should return carac. What is the running time of your algorithm?

Input

• X = <x₁, x₂, .... , x_m>

Output

• the longest palindrome of X

调用LCS算法

针对这个问题，完全可以使用LCS最长公共子序列问题的算法进行求解，将所给字符串A进行倒置得到字符串B，计算A，B的最长公共子序列即可。

动态规划算法

引用：算法导论 — 思考题15-2 最长回文子序列

优化子结构

Theorem

假设P[1..k]=< p1, p2 ,…,pk> 是字符串S[1..n]=s1, s2 ,…, sn的一个最长回文子序列，那么：

• if s1 == sn, then s1 = p1, sn = pn, P[2..k-1]是S[2..-1]的一个最长回文子序列
• if s1 != sn, s1 != p1, then P[1..k]是S[2..k]的一个最长回文子序列
• if s1 != sn, s1 != pn, then P[1..k]是S[1..k-1]的一个最长回文子序列

这一问题的优化子结构，及其类似于LCS问题的优化子结构，都需要依据情况进行想处理。

Proof

• 如果s1 != p1（s2 != p2这两个其实是一个意思），那么，完全可以将s1，s2加在P[1..k]两侧，构造一个比当前最长回文子序列更长的回文子序列。
• 如果P[2..k-1]不是S[2..k-1]的一个最长回文子序列，即存在回文子序列Q是S[2..k-1]的一个最长回文子序列，且，|Q| > k-2。那么，可以在Q两端加入s1==sn，得到回文子序列M，|M| > k，这与P[1..k]=< p1, p2 ,…,pk> 是字符串S[1..n]=s1, s2 ,…, sn的一个最长回文子序列矛盾，假设不成立。
• 至于2&&3点，反证法及其简单。

递归地定义代价方程

定义c[i,j ]为s[i,j] = <s_i, s_i+1,..., s_j>的最长回文子序列的长度。

\[c[i,j]= \left\{ \begin{array}{rcl} & 0 & j < i \\ & 1 & j = i \\ & c[i+1,j-1] & j>i,s_{i} = s_{j} \\ & max{c[i,j-1],c[i+1,j]} & j>i,s_{i}\neq s_{j} \end{array} \right. \]

重叠子问题

要计算	需计算	需计算	需计算
c[i,j]	c[i+1,j-1]	c[i,j-1]	c[i+1,j]
c[i+1,j-1]	c[i+2,j-2]	c[i+1,j-2]	c[i+2,j-1]
c[i,j-1]	c[i+1,j-2]	c[i,j-2]	c[i+1,j-1]
c[i+1,j]	c[i+2,j+1]	c[i+1,j-1]	c[i+2,j]

计算优化解的代价的伪代码

下图为优化解的填充顺序，黄》绿》蓝》橘》灰》白

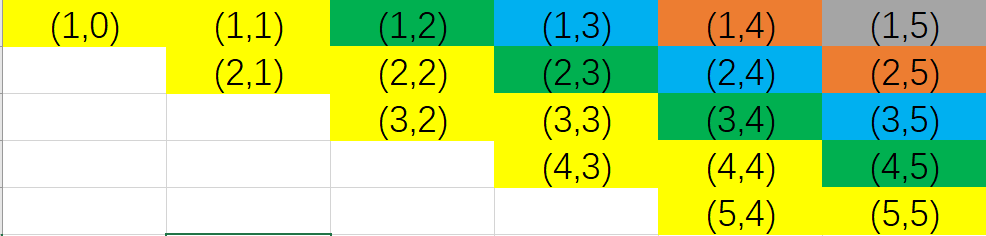
由此可以构建出计算优化解的算法(bottomup)：

LPS_LENTH(x)
n = x.length
let s[1..n,1..n] and c[1..n,1..n]be a new array
for i = 1 to n do
    s[i,i] = 1; 
    s[i,i-1] = 0;
for l = 1 to n - 1 do 
    for i = 1 to n - l
        j = i + l
        if xi == xj
            s[i,j] = s[i+1,j-1] + 2
            c[i,j] = '↙'
        else 
            if s[i+1,j] > s[i,j-1]
               s[i,j] = s[i+1,j]
               c[i,j] = '↓'
            else
               s[i,j] = s[i,j-1]
               c[i,j] = '←'

构造优化解的伪代码

Print_LPS(x,c,i,j)
if i == j 
    print x[i]
    return
if c[i,j] == '↙'
    print x[i];
    Print_LPS(x,c,i+1,j-1);
    print x[i];
else if c[i,j] == '↓'
    Print_LPS(x,c,i+1,j);
else if c[i,j] = '←'
    Print_LPS(x,c,i,j-1);

算法复杂度分析

计算优化解的代价的算法时间复杂度为：O(n²)

构造优化解算法的时间复杂度为：O(n)

代码

#include<stdio.h>
#include<string.h>

#define N 9

void LPS_LENGTH(char* x);
void Print_LPS(char* x, char c[N + 1][N + 1], int i, int j);

void main() {
	char x[N + 1] = { ' ', 'c', 'h', 'a', 'r', 'a', 'c', 't','e','r' };
	for (int i = 1; i <= N; i++) {
		printf("%c	", x[i]);
	}
	printf("\n");
	
	LPS_LENGTH(x);

}

void LPS_LENGTH(char* x) {
	int s[N + 1][N + 1];
	char c[N + 1][N + 1];
	memset(s, 0, sizeof(int) * (N + 1) * (N + 1));
	memset(c, '0', sizeof(char) * (N + 1) * (N + 1));
	for (int i = 1; i <= N; i++) {
		s[i][i] = 1;
		s[i][i - 1] = 0;
	}
	for (int l = 1; l <= N - 1; l++) {
		for (int i = 1; i <= N - l; i++) {
			int j = i + l;
			if (x[i] == x[j]) {
				s[i][j] = s[i + 1][j - 1] + 2;
				//c[i][j] = '↙';
				c[i][j] = '1';
			}
			else {
				if (s[i + 1][j] > s[i][ j - 1]) {
					s[i][j] = s[i + 1][j];
					//c[i][j] = '↓';
					c[i][j] = '2';
				}
				else {
					s[i][j] = s[i][j - 1];
					//c[i][j] = '←';
					c[i][j] = '3';
				}
			}
		}
	}
	for (int i = 1; i <= N; i++) {
		for (int j = 1; j <= N; j++)
			printf("%d	", s[i][j]);
		printf("\n");
	}
	printf("\n");
	printf("\n");
	for (int i = 1; i <= N; i++) {
		for (int j = 1; j <= N; j++)
			printf("%d	", s[i][j]);
		printf("\n");
	}
	printf("\n");
	printf("\n");
	Print_LPS(x, c, 1, N);
}

void Print_LPS(char *x, char c[N+1][N+1], int i, int j) {
	if (i == j) {
		printf("%c	", x[i]);
		return;
	}
	if (c[i][j] == '1') {
		printf("%c	", x[i]);
		Print_LPS(x, c, i + 1, j - 1);
		printf("%c	", x[i]);
	}
	else if(c[i][j] == '2')
		Print_LPS(x, c, i + 1, j);
	else 
		Print_LPS(x, c, i, j - 1);
}