算法导论15章答案

15.1-1

Show that equation (15.4) follows from equation (15.3) and the initial condition T(0) = 1.

\[\begin{aligned} T(n) & = 1 + T(1) + T(2) + ... + T(n-2) + T(n-1). \\ T(n-1) & = 1 + T(1) + T(2) + ... + T(n-2). \\ T(n) & = 2^{1}*T(n-1) = 2^{2}*T(n-2) = ... =2^{i}*T(n - i)\\ \\ 可令 & T(n - i) = 1，那么i = n\\ 则 & T(n) = 2^{n} \end{aligned} \]

15.1-2

Show, by means of a counterexample, that the following “greedy” strategy does not always determine an optimal way to cut rods. Define the density of a rod of length i to be pi / i, that is, its value per inch. The greedy strategy for a rod of length n cuts off a first piece of length i,where 1 <= i <= n, having maximum density. It then continues by applying the greedy strategy to the remaining piece of length n - i .

length i	1	2	3	4
price Pi	1	5	8	9
density Ci	1	2.5	2.6666....	2.25

显然，C₃ > C₂ > C₄ > C₃

那么，依照上面的贪心算法，分割方式为 4 = 3 + 1，此时的总价值为9。而存在 4 = 2 + 2，此时的总价值为10。

15.1-3

Consider a modification of the rod-cutting problem in which, in addition to a price pi for each rod, each cut incurs a fixed cost of c. The revenue associated with a solution is now the sum of the prices of the pieces minus the costs of making the cuts. Give a dynamic-programming algorithm to solve this modified problem.

MEMOIZED-CUT-ROD(p,n)
1. let r[0...n] and s[0...n] be a new array
2. for i = 0 to n
3.    r[i] = -∞
4. return MEMOIZED-CUT-ROD-AUX(p,n,r,s) and s

MEMOIZED-CUT-ROD-AUX(p,n,r,s)
1. if r[n] >= 0
2.    return r[n]
3. if n == 0
4.    q = 0 
5. else
6.    q = -∞
7.    for i = 1 to n - 1
8.        m = p[i] + MEMOIZED-CUT-ROD-AUX(p,n-i,r) - c
9.        if q < m
10.           q = m
11.           s[n] = i
12.   if q < p[n]
13.      q = p[n];
14.      s[n] = n;
15. r[n] = q
16. return q

BOTTOM-UP-CUT-ROD(p,n)
1. let r[0...n] and s[0...n] be a new array 
2. r[0] = 0 
3. for j = 1 to n 
4.     q = -∞
5.     for i = 1 to j-1 
6.        if q < p[i] + r[j - i] - c 
7.           q = p[i] + r[j - i] - c
8.           s[j] = i
9.     if q < P[j]
10.       q = p[j]
11.       s[j] = j
12.    r[j] = q 
13. return r[n] and s

15.1-4

Modify MEMOIZED-CUT-ROD to return not only the value but the actual solution, too.

MEMOIZED-CUT-ROD(p,n)
1. let r[0...n] and s[0...n] be a new array
2. for i = 0 to n
3.    r[i] = -∞
4. s[0] = 0
5. return MEMOIZED-CUT-ROD-AUX(p,n,r,s) and s

MEMOIZED-CUT-ROD-AUX(p,n,r,s)
1. if r[n] >= 0
2.    return r[n]
3. if n == 0
4.    q = 0 
5. else
6.    q = -∞
7.    for i = 1 to n
8.      m = p[i] + MEMOIZED-CUT-ROD-AUX(p,n-i,r))
9.      if q < m
10.         q = m
11.         s[n] = i
12. r[n] = q
13. return q

15.1-5

The Fibonacci numbers are defined by recurrence (3.22). Give an O(n)time dynamic-programming algorithm to compute the n_th Fibonacci number. Draw the subproblem graph. How many vertices and edges are in the graph?

这道题严格来讲并不是动态规划问题，下面是采用动态规划保存解的方式进行处理的算法，其实只需要两个变量保存前面两个值即可，不用这么麻烦。

至于其时间复杂度，显然是O(n).

top-down

Fibonacci-number(n)
let r[0...n] be a new array
for i = 0 to n
    r[i] = -1
return Fibonacci-run-number(n-1,r) + Fibonacci-run-number(n-2,r)

Fibonacci-run-number(n,r)
if r[n] != -1 return r[n]
if n = 0 
    r[n] = 0
else if n = 1 
    r[n] = 1
else 
    r[n] = Fibonacci-run-number(n-1) + Fibonacci-run-number(n-2)
return r[n]

bottom-up

Fibonacci-number(n)
1. let r[0...n] and s[0...n] be a new array 
2. r[0] = 0
3. r[1] = 1
4. for q = 2 to n
5.    r[q] = r[q-1] + r[q-2]
6. return r[n]

15.2-2

Give a recursive algorithm MATRIX-CHAIN-MULTIPLY(A,s,i,j) that actually performs the optimal matrix-chain multiplication, given the sequence of matrices {A₁,A₂,...,A_n} , the s table computed by MATRIX-CHAIN-ORDER, and the indices i and j . (The initial call would be MATRIX-CHAIN-MULTIPLY(A,s,1,n)

MATRIX-CHAIN-MULTIPLY(A,s,i,j)
1. if i == j
2.    return A[i]
3. else
4.    return MATRIX-CHAIN-MULTIPLY(A,s,i,s[i,j]) * MATRIX-CHAIN-MULTIPLY(A,s,s[i,j]+1,j)

15.2-3 未完成

Use the substitution method to show that the solution to the recurrence (15.6) is Ω(2ⁿ)

15.2-4

Describe the subproblem graph for matrix-chain multiplication with an input chain of length n. How many vertices does it have? How many edges does it have, and which edges are they?

方法一：看矩阵直接归纳

计算顶点个数，可以类比矩阵的填充，进行构思。一共(n² + n) / 2个子问题，每一个子问题A_i...A_j一共有 2*(j - i) 条出边。

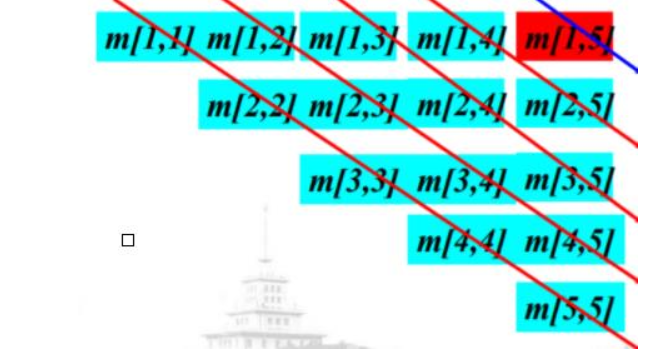
对于整个图的边数，可以借助填充矩阵进行思考，即：

主对角线上的第0条对角线，共有n个元素，其中每个元素有0条出边
主对角线上的第1条对角线，共有(n-1)个元素，其中每个元素有1条出边
主对角线上的第2条对角线，共有(n-2)个元素，其中每个元素有2条出边
......
主对角线上的第n-2条对角线，共有2个元素，其中每个元素有n-2条出边
主对角线上的第n-1条对角线，共有1个元素，其中每个元素有n-1条出边
即，总的边数为：

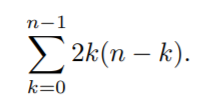
方法二：形式化证明

摘录他人答案

 
 The subproblem graph for matrix chain multiplication has a vertex for each pair (i, j) such that 1 ≤ i ≤ j ≤ n, corresponding to the subproblem of finding the optimal way to multiply A<sub>i</sub>A<sub>i+1</sub> · · · A<sub>j</sub> . There are n(n − 1)/2 + n vertices. 

 Vertex (i, j) is connected by an edge directed to vertex (k, l) if k = i and k ≤ l < j or l = j and i < k ≤ j. A vertex (i, j) has outdegree 2(j − i). **看不懂**

 There are n − k vertices such that j − i = k, so the total number of edges is nX−1 k=0 2k(n − k).

对于上面问题的补充

对于上文求解的可能细节的补充，以使用排列组合进行处理，典型的从n个物体中选取两个物体，同时还需要加上 i = j的情况。那么一共 n(n − 1)/2 + n = (n² + n) / 2个子问题。
对于依赖的子问题，另一种思考方式，对于一个顶点( i,j )，要寻找其依赖的子问题，实际上就是寻找k，将其矩阵列进行划分为 ( i,k ) &&( k+1,j )，i≤k≤j - 1，故而，一共存在 j - 1 - (i - 1) = j - i 种划分，那么一共有2*( j-i )个子问题。

15.2-5

Let R(i, j) be the number of times that table entry m[i, j] is referenced while computing other table entries in a call of MATRIX-CHAIN-ORDER. Show that the total number of references for the entire table is
(Hint: You may find equation (A.3) useful.)

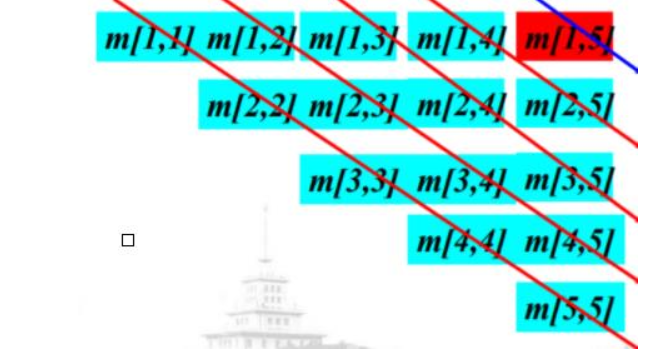
对于此问题而言，可以考虑采用矩阵填充进行判断。

主对角线上的第0条对角线，共有n个元素，其中每个元素被引用(n-1)次
主对角线上的第1条对角线，共有(n-1)个元素，其中每个元素被引用(n-2)次
主对角线上的第2条对角线，共有(n-2)个元素，其中每个元素被引用(n-3)次
......
主对角线上的第n-2条对角线，共有2个元素，其中每个元素被引用1次
主对角线上的第n-1条对角线，共有1个元素，其中每个元素被引用0次
即，总的引用次数为：1 * 2 + 2 * 3 + ... + (n-1)*(n)

而

\[\begin{aligned} & 1 * 2 + 2 * 3 + ... + (n)*(n+1)\\ = & (1 + 2 + 3 + ... + n) + (1^{2} + 2^{2}+ ... + n^{2}) \\ = & \frac{n(n+1)}{2} + \frac{n(n+1)(2n+1)}{6}\\ = & \frac{n(n+1)(n+2)}{3} \end{aligned} \]

而

\[1 * 2 + 2 * 3 + ... + (n-1)*(n) = \frac{( n-1 )( n )( n+1 ) }{ 3} = \frac{n^2-n}{3} \]

另一种更为形式化的证明：

We count the number of times that we reference a different entry in m than the one we are computing, that is, 2 times the number of times that line 10 runs.

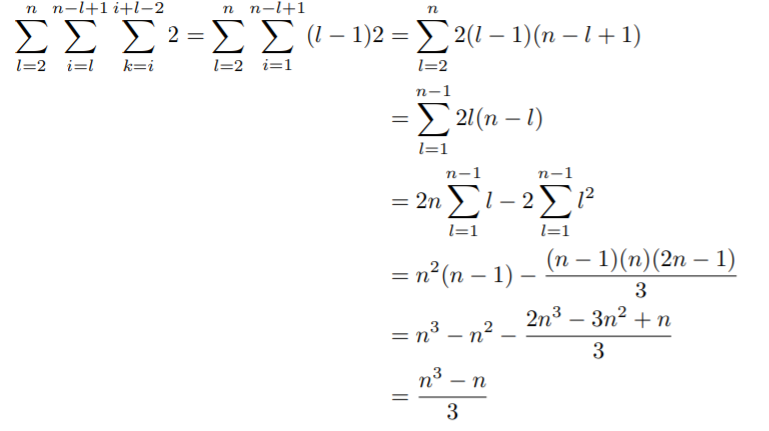
15.2.6

Show that a full parenthesization of an n-element expression has exactly n-1 pairs of parentheses.

定义, A product of matrices is fully parenthesized, if it is either a single matrix or the product of two fully parenthesized matrix products, surrounded by parentheses.

对于parenthesization的定义，我们可以将之递归地定义：

a single matrix is fully parenthesized.
A * B is fully parenthesized，if A is fully parenthesized and B is fully parenthesized.

证明：

We proceed by induction on the number of matrices. A single matrix has no pairs of parentheses. Assume that a full parenthesization of an n-element expression has exactly n − 1 pairs of parentheses. Given a full parenthesization of an n+ 1-element expression, there must exist some k such that we first multiply B = A₁ · · · A_k in some way, then multiply C = A_k+1 · · · A_n+1 in some way, then multiply B and C. By our induction hypothesis, we have k − 1 pairs of parentheses for the full parenthesization of B and n + 1 − k − 1 pairs of parentheses for the full parenthesization of C. Adding these together, plus the pair of outer parentheses for the entire expression, yields k−1+n+ 1−k−1+ 1 = (n+ 1)−1 parentheses, as desired.

个人所进行的证明时，对于归纳的第3步的往证出现问题，这里它使用了一个矩阵链乘的基本定理：即多个矩阵相乘，最终一定会归结到两个矩阵的乘法。另外对于该英文解释中的细节值得注意。

15.3-1 疑问

Which is a more efficient way to determine the optimal number of multiplications in a matrix-chain multiplication problem: enumerating all the ways of parenthesizing the product and computing the number of multiplications for each, or running RECURSIVE-MATRIX-CHAIN? Justify your answer.

下面是摘抄网络上的题解，由你自己进行评判。

这里感觉在某种程度上是不可以细究的，因为其并没有给出究竟应当计算的基础是哪种运算的数量。这里将默认为所有运算的数量，包括赋值，但不包括比较。

这里会T(n)会涉及c 的问题。对于n = 1，为1-2行的至多运行次数，对于n>1，个人认为第一个c所指示的是6-7行的运行次数，第二个c所指示的是第5行的乘法次数，当然了可能存在某些不合理性，但是，由于取一个上界，那么，对于常数的扩大也是可以的。（这一部分不是很确定）

下面是另一种思考方式：

其中需要进行深究的是，究竟判断2组n个数据的大小算法复杂度低环视判断n²个数据的的算法复杂度低呢？

15.3-2

Draw the recursion tree for the MERGE-SORT procedure from Section 2.3.1 on an array of 16 elements. Explain why memoization fails to speed up a good divideand-conquer algorithm such as MERGE-SORT.

递归树的形式化描述：

Let [i..j ] denote the call to Merge Sort to sort the elements in positions i through j of the original array. The recursion tree will have [1..n] as its root, and at any node [i..j ] will have [i..(j − i)/2] and [(j − i)/2 + 1..j] as its left and right children, respectively. If j − i = 1, there will be no children.

备忘不可以加速归并算法的原因：

The memoization approach fails to speed up Merge Sort because the subproblems aren’t overlapping. Sorting one list of size n isn’t the same as sorting another list of size n, so there is no savings in storing solutions to subproblems since each solution is used at most once.

15.3-3

Consider a variant of the matrix-chain multiplication problem in which the goal is to parenthesize the sequence of matrices so as to maximize, rather than minimize, the number of scalar multiplications. Does this problem exhibit optimal substructure?

仍然表现出优化子结构的性质，可以使用spilt进行说明。

15.3-4

As stated, in dynamic programming we first solve the subproblems and then choose which of them to use in an optimal solution to the problem. Professor Capulet claims that we do not always need to solve all the subproblems in order to find an optimal solution. She suggests that we can find an optimal solution to the matrix chain multiplication problem by always choosing the matrix A_k at which to split the subproduct A_i, A_i+1 ,..., A_j (by selecting k to minimize the quantity p_i-1p_kp_j ) before solving the subproblems. Find an instance of the matrix-chain multiplication problem for which this greedy approach yields a suboptimal solution.

例子1：

此处的判断方法与动态规划算法中的判断方法相比，其缺少了关于其拆分之后的两个矩阵链的代价，当比较两种分割方式时，如果这两个矩阵链的代价相差大于p_i-1p_kp_j的相差，便会对最终的选择造成影响。

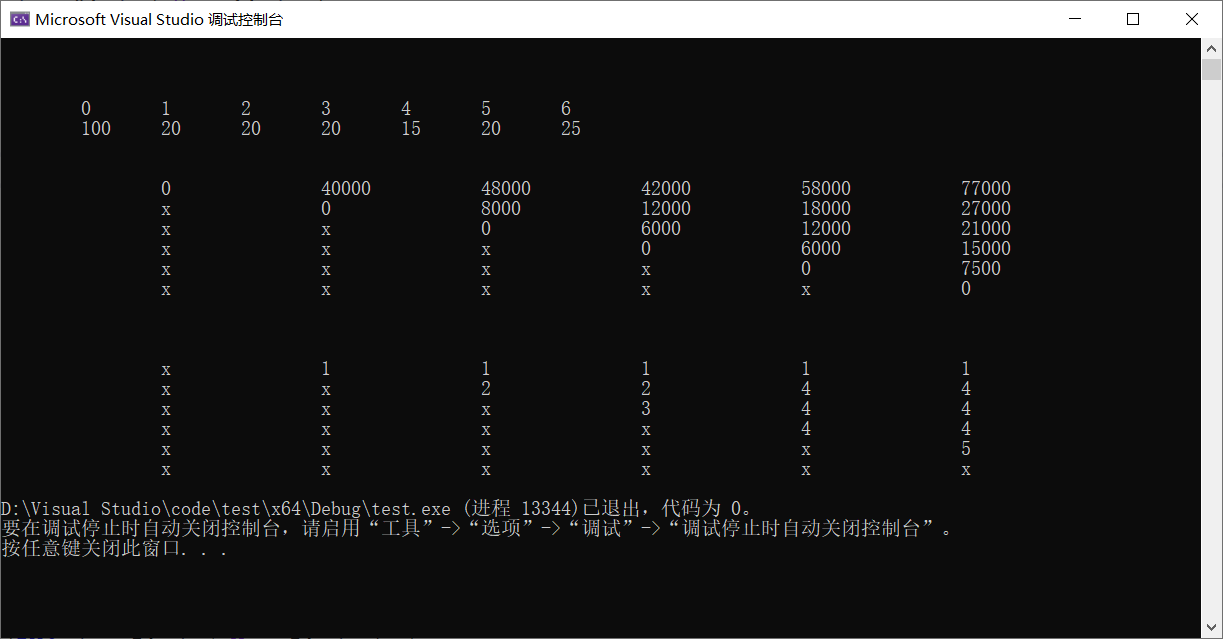
源代码如下

#include<stdio.h>
#include<stdlib.h>
#define n 6

void main() {
	long P[n + 1] = {100,20,20,20,15,20,25};
	//int P[n + 1] = { 30,35,15,5,10,20,25 };
	long m[n + 1][n + 1];
	long s[n + 1][n + 1];
	for (int i = 0; i < n + 1; i++) {
		for (int j = 0; j < n + 1; j++) {
			s[i][j] = -1;
			m[i][j] = -1;
		}
	}
	for (int i = 1; i <= n; i++) {
		m[i][i] = 0;
	}
	for (int l = 2; l <= n; l++) {
		for (int i = 1; i <= n - l + 1; i++) {
			int j = i + l - 1;
			m[i][j] = INT_MAX;
			for (int k = i; k <= j - 1; k++) {
				long q = m[i][k] + m[k + 1][j] + P[i - 1] * P[k] * P[j];
				if (q < m[i][j]) {
					m[i][j] = q;
					s[i][j] = k;
				}
			}
		}
	}
	printf("\n"); 
	printf("\n"); 
	printf("\n");
	for (int i = 0; i < n + 1; i++)
		printf("	%d", i);
	printf("\n");
	for (int i = 0; i < n + 1; i++)
		printf("	%d", P[i]);
	printf("\n");
	printf("\n");
	printf("\n");
	for (int i = 1; i < n+1; i++) {
		for (int j = 1; j < n + 1; j++) {
			if (m[i][j] != -1)
				printf("		%d", m[i][j]);
			else
				printf("		x");
		}
		printf("\n");
	}
	printf("\n");
	printf("\n");
	printf("\n");
	for (int i = 1; i < n+1; i++) {
		for (int j = 1; j < n + 1; j++) {
			if (s[i][j] != -1)
				printf("		%d", s[i][j]);
			else
				printf("		x");
		}
		printf("\n");
	}
}

例子2

Suppose that we are given matrices A₁, A₂, A₃, and A₄ with dimensions such that p₀, p₁, p₂, p₃, p₄ = 1000, 100, 20, 10, 1000. Then p0pkp4 is minimized when k = 3, so we need to solve the subproblem of multiplying A₁A₂A₃ and also A₄ which is solved automatically. By her algorithm, this is solved by splitting at k = 2. Thus, the full parenthesization is (((A₁A₂)A₃)A₄). This requires 1000 · 100 · 20 + 1000 · 20 · 10 + 1000 · 10 · 1000 = 12, 200, 000 scalar multiplications. On the other hand, suppose we had fully parenthesized the matrices to multiply as ((A₁(A₂A₃))A₄). Then we would only require 100 · 20 · 10 + 1000 · 100 · 10 + 1000 · 10 · 1000 = 11, 020, 000 scalar multiplications, which is fewer than Professor Capulet’s method. Therefore her greedy approach yields a suboptimal solution.

15.3-5

Suppose that in the rod-cutting problem of Section 15.1, we also had limit l_i on the number of pieces of length i that we are allowed to produce, for i = 1, 2 ,..., n. Show that the optimal-substructure property described in Section 15.1 no longer holds.

一定要理解清楚题意，其增加的限制条件是队友长度是i的棒的数量做出了规定，而这显然就破坏子问题的独立性。

The optimal substructure property doesn’t hold because the number of pieces of length i used on one side of the cut affects the number allowed on the other. That is, there is information about the particular solution on one side of the cut that changes what is allowed on the other. To make this more concrete, suppose the rod was length 4, the values were l₁ = 2, l₂ = l₃ = l₄ = 1, and each piece has the same worth regardless of length. Then, if we make our first cut in the middle, we have that the optimal solution for the two rods left over is to cut it in the middle, which isn’t allowed because it increases the total number of rods of length 1 to be too large.

15.3-6 未完成

Imagine that you wish to exchange one currency for another. You realize that instead of directly exchanging one currency for another, you might be better off making a series of trades through other currencies, winding up with the currency you want. Suppose that you can trade n different currencies, numbered 1; 2; ::: ; n, where you start with currency 1 and wish to wind up with currency n.You are given, for each pair of currencies i and j , an exchange rate rij , meaning that if you start with d units of currency i , you can trade for drij units of currency j . A sequence of trades may entail a commission, which depends on the number of trades you make. Let ck be the commission that you are charged when you make k trades. Show that, if ck D 0 for all k D 1; 2; ::: ; n, then the problem of finding the best sequence of exchanges from currency 1 to currency n exhibits optimal substructure. Then show that if commissions ck are arbitrary values, then the problem of finding the best sequence of exchanges from currency 1 to currency n does not necessarily exhibit optimal substructure.

对于货币序列(i,i+1,...,j)，定义所有两种货币的利率的集合为A，将货币i 交换为货币j 的的最优解的交换序列为(r₁, r₂, ,...,r_j-i)，r_i ∈ A，r_i != r_j，且，r_i 表示的得到的货币类型与r_i+1中被交易的货币类型相同。那么，

15.4-1

Determine an LCS of {1, 0, 0, 1, 0, 1, 0, 1} and {0, 1, 0, 1, 1, 0, 1, 1, 0}.

		0	1	2	3	4	5	6	7	8
			`1`	`0`	`0`	`1`	`0`	`1`	`0`	`1`
0		0	0	`0`	0	0	0	0	0	0
2	`0`	`0`	0	1	`1`	1	1	1	1	1
3	`1`	0	`1`	1	1	`2`	2	2	2	2
4	`0`	0	1	`2`	2	2	`3`	3	3	3
5	`1`	0	1	`2`	`2`	3	`3`	4	4	4
6	`1`	0	1	`2`	2	`3`	3	`4`	4	5
7	`0`	0	1	2	`3`	3	`4`	4	`5`	5
8	`1`	0	1	2	3	`4`	`4`	5	`5`	6
9	`1`	0	1	2	3	4	4	`5`	5	`6`
10	`0`	0	1	2	3	4	5	5	`6`	`6`

公共字符串为：0，1，0，1，0，1 && 1，0，1，0，1，0

其实公共字符串不止一条，可以在上述表格中找到其他的路径，由此构造的公共字符串也可以是最优解

15.4-2

Give pseudocode to reconstruct an LCS from the completed c table and the original sequences X =< x₁, x₂, ..., x_m> and Y = <y₁, y₂, ... ,y_n> in O(m + n) time, without using the b table.

PRINT-LCS(b,X,Y,i,j)
if i == 0 or j == 0
    return 0
if X[i] == Y[j] then
    PRINT-LCS(b,X,Y,i-1,j-1)
    print X[i]
else 
    if(b[i][j] == b[i][j-1])
        PRINT-LCS(b,X,Y,i,j-1)
    else
        PRINT-LCS(b,X,Y,i-1,j)

显然，其算法时间复杂度为O(m+n)，在每一次调用中，将至少减少i或者j中的任意一个。这与原构造最优解的算法是类似的，只是在判断条件上改变了判断条件，实际的判断代价改变非常小。

15.4-3

Give a memoized version of LCS-LENGTH that runs in O(mn) time.

伪代码

LCS-LENGTH( X, Y, m ,n )
Let b[0..m][0..n] be an new array
for i = 1 to m
    for j = 1 to n
        b[i][j] = -1
return LCS-LENGTH-AUX(X, Y, m ,n ,b ,s)

        

LCS-LENGTH-AUX(X, Y, i ,j ,b ,s)
if b[i][j] != -1
    return b[i][j] && s
if i = 0 || j = 0
    b[i][j] = 0
else if X[i] == X[j]
    b[i][j] = LCS-LENGTH-AUX(X, Y, i-1 ,j-1 ,b ,s) + 1
else 
    b[i][j] = LCS-LENGTH-AUX(X, Y, i-1 ,j ,b ,s) > LCS-LENGTH-AUX(X, Y, i ,j-1 ,b ,s) ? LCS-LENGTH-AUX(X, Y, i ,j-1 ,b ,s):LCS-LENGTH-AUX(X, Y, i-1 ,j ,b ,s)
return b[i][j]

代码

下面是输出结果，极为有趣的是，从这里可以看出这两种构造方法的区别，一种完全遍历，一种只会遍历其需要的单位。

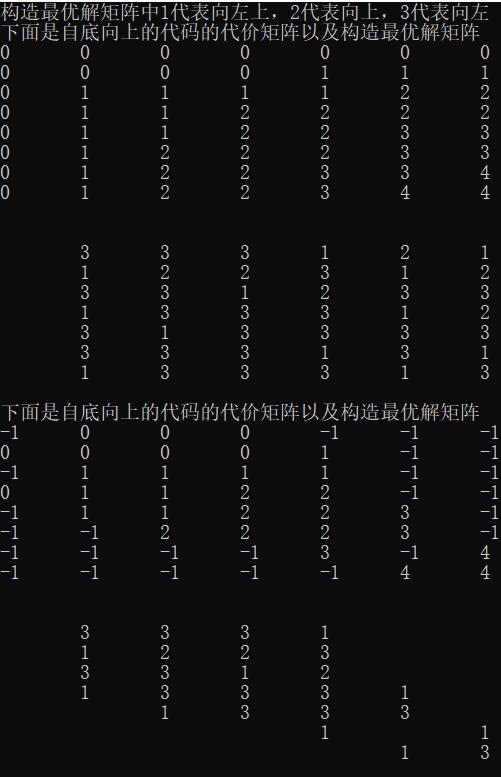
#include<stdio.h>
#include<string.h>

#define M 7
#define N 6

void LCS_length_bottomup(char* x, char* y);
void LCS_length_updown(char* x, char* y);
int LCS_length_AUX(char* x, char* y, int i, int j, int b[M + 1][N + 1], char s[M + 1][N + 1]);

void main() {
	char x[M + 1] = { ' ', 'A', 'B', 'C', 'B', 'D', 'A', 'B' };
	char y[N + 1] = { ' ','B','D','C','A','B','A' };
	LCS_length_bottomup(x, y);
	LCS_length_updown(x, y);
}

void LCS_length_updown(char* x, char* y) {
	int b[M + 1][N + 1];
	char s[M + 1][N + 1];
	memset(b, -1, (M + 1) * (N + 1) * sizeof(int));
	memset(s, ' ', (M + 1) * (N + 1) * sizeof(char));
	LCS_length_AUX(x, y, M, N, b, s);
	for (int i = 0; i <= M; i++) {
		for (int j = 0; j <= N; j++) {
			printf("%d	", b[i][j]);
		}
		printf("\n");
	}
	printf("\n");
	for (int i = 0; i <= M; i++) {
		for (int j = 0; j <= N; j++) {
			printf("%c	", s[i][j]);
		}
		printf("\n");
	}
	printf("\n");
}

int LCS_length_AUX(char* x, char* y,int i, int j, int b[M + 1][N + 1], char s[M + 1][N + 1]){
	if (b[i][j] != -1) return b[i][j];
	if (i == 0 || j == 0) {
		b[i][j] = 0;
	}
	else if (x[i] == y[j]) {
		b[i][j] = LCS_length_AUX(x, y, i-1, j-1, b, s) + 1;
		s[i][j] = '1';//左上
	}
	else {
		int p = LCS_length_AUX(x, y, i , j - 1, b, s);
		int q = LCS_length_AUX(x, y, i - 1, j , b, s);
		if (p > q) {
			b[i][j] = p;
			s[i][j] = '2';//上
		}
		else {
			b[i][j] = q;
			s[i][j] = '3';//下
		}
	}
	return b[i][j];
}

void LCS_length_bottomup(char *x, char *y) {
	int b[M + 1][N + 1];
	char s[M + 1][N + 1];
	memset(b, -1, (M + 1) * (N + 1) * sizeof(int));
	memset(s, ' ', (M + 1) * (N + 1) * sizeof(char));
	for (int i = 0; i <= M; i++) 
		b[i][0] = 0;
	for (int i = 0; i <= N; i++)
		b[0][i] = 0;
	for (int i = 1; i <= M; i++) {
		for (int j = 1; j <= N; j++) {
			if (x[i] == y[j]) {
				b[i][j] = b[i - 1][j - 1] + 1;
				s[i][j] = '1';//左上
			}
			else if (b[i - 1][j] < b[i][j - 1]) {
				b[i][j] = b[i][j - 1];
				s[i][j] = '2';//上
			}
			else {
				b[i][j] = b[i - 1][j];
				s[i][j] = '3';//左
			}
		}
	}
	for (int i = 0; i <= M; i++) {
		for (int j = 0; j <= N; j++) {
			printf("%d	", b[i][j]);
		}
		printf("\n");
	}
	printf("\n");
	for (int i = 0; i <= M; i++) {
		for (int j = 0; j <= N; j++) {
			printf("%c	", s[i][j]);
		}
		printf("\n");
	}
	printf("\n");
}

15.4-4

Show how to compute the length of an LCS using only 2* min(m, n) entries in the c table plus O(1) additional space. Then show how to do the same thing, but using min(m, n) entries plus O(1) additional space.

伪代码：2 min(m, n) entries in the c table plus O(1) additional space*

PS：不得不说，取余真是个好东西，原本以为会很长的

LCS-length_bottomup(X, Y)
m = length(X);
n = length(Y);
let p[0..1][1...min(m,n)]  be a new array
for i = 1 to min(m,n) do
    p[0,i] = 0
for i = 1 To max(m,n) Do
     For j = 1 To min(m,n) Do
          If Xi == Yj
             Then p[i%2,j] = p[(i-1)%2,j-1]+1;
          Else If p[(i-1)%2,j]  <  C[i%2,j-1]
             Then p[i%2,j] = p[(i-1)%2,j];
          Else     
                  p[i%2,j] = p[i%2,j-1];
Return p[max(m,n),min(m,n)]

下面是实际代码

#include<stdio.h>
#include<string.h>

#define M 7
#define N 6

void LCS_length_2min(char* x, char* y);

void main() {
	char x[M + 1] = { ' ', 'A', 'B', 'C', 'B', 'D', 'A', 'B' };
	char y[N + 1] = { ' ','B','D','C','A','B','A' };
	LCS_length_2min(x, y);
}

void LCS_length_2min(char* x, char* y) {
	// M >= N
	int P[2][N + 1];
	for (int i = 0; i <= N; i++) {
		P[0][i] = 0;
	}
	P[1][0] = 0;
	for (int i = 1; i <= M; i++) {
		for (int j = 1; j <= N; j++) {
			if (x[i] == y[j]) {
				P[i % 2][j] = P[(i - 1) % 2][j - 1] + 1;
			}
			else if (P[(i - 1) % 2][j] > P[(i) % 2][j - 1]) {
				P[i % 2][j] = P[(i - 1) % 2][j];
			}
			else {
				P[i % 2][j] = P[(i) % 2][j - 1];
			}
		}
	}
	printf("%d\n", P[M % 2][N]);
}

伪代码： min(m, n) entries in the c table plus O(1) additional space

LCS-length_bottomup(X, Y)
m = length(X);
n = length(Y);
int Leftentry = 0;//保存当前计算代价的左上代价
int LeftUpentry = 0;
//保存当前代价的左代价，其实可以不使用，直接比较p[j-1]和p[j]，但是为了保证代码的统一性，即0的情况，故采用一个单独变量
let P[1...min(m,n)]  be a new array;
for i = 1 to min(m,n) do
    P[i] = 0;
for i = 1 To max(m,n) Do
     For j = 1 To min(m,n) Do
          If Xi == Yj
             Then transition = P[j];
                  //由于下一次循环需要使用被覆盖的P[j],但又不可以直接赋值到LeftUpentry中，设置过渡变量
                  P[j] = LeftUpentry + 1;
                  LeftUpentry = transition;
                  Leftentry = P[j];
          Else If Leftentry  <  P[j]
             Then LeftUpentry = P[j];
                  Leftentry = P[j];
          Else     
                  LeftUpentry = P[j];
                  P[j] = Leftentry;
                  Leftentry = P[j];
     Leftentry = 0;
     LeftUpentry = 0;
Return p[min(m,n)]

下面是实际代码

#include<stdio.h>
#include<string.h>

#define M 7
#define N 6

void LCS_length_min(char* x, char* y);

void main() {
	char x[M + 1] = { ' ', 'A', 'B', 'C', 'B', 'D', 'A', 'B' };
	char y[N + 1] = { ' ','B','D','C','A','B','A' };
	LCS_length_min(x, y);
}

void LCS_length_min(char* x, char* y) {
	//M > N
	int Leftentry = 0;
	int LeftUpentry = 0;
	int P[N + 1];
	for (int i = 1; i <= N; i++) {
		P[i] = 0;
	}
	for (int i = 1; i <= M; i++) {
		for (int j = 1; j <= N; j++) {
			if (x[i] == y[j]) {
				int trans = P[j];
				P[j] = LeftUpentry + 1;
				LeftUpentry = trans;
				Leftentry = P[j];
			}
			else if (Leftentry < P[j]) {
				Leftentry = P[j];
				LeftUpentry = P[j];
			}
			else {
				LeftUpentry = P[j];
				P[j] = Leftentry;
				Leftentry = P[j];
			}
		}
        //这里为调试信息，可以以原来矩阵的格式打印出来
		for (int i = 1; i <= N; i++) {
			printf("%d	", P[i]);
		}
		printf("\n");

		Leftentry = 0;
		LeftUpentry = 0;
	}
	printf("%d\n", P[N]);
}

15.4-5 未完成

Give an O(n²)-time algorithm to find the longest monotonically increasing subsequence of a sequence of n numbers.

算法可以给出，但是关于最优解的证明无法给出，因为一个最长递增子序列的前半部分，并不一定是最优解。

15.4-6 未完成

Give an O(nlgn) time algorithm to find the longest monotonically increasing subsequence of a sequence of n numbers. (Hint: Observe that the last element of a candidate subsequence of length i is at least as large as the last element of a candidate subsequence of length i - 1. Maintain candidate subsequences by linking them through the input sequence.)

15.5-1

Write pseudocode for the procedure CONSTRUCT-OPTIMAL-BST(root) which, given the table root, outputs the structure of an optimal binary search tree. For the example in Figure 15.10, your procedure should print out the structure

corresponding to the optimal binary search tree shown in Figure 15.9(b).

伪代码

CONSTRUCT-OPTIMAL-BST(root) 
n = root[0].length
print K {root[1,n]} is the root
Print-BST(root,1,n)

Print-BST(root,i,j)
if (i <= root[i,j]-1) 
   print k {root[i,root[i,j]-1]} is the left child of k {root[i,j]}
   print-BST(root,i,root[i,j]-1)
else
   print d {root[i,j]-1} is the left child of k {root[i,j]}
if (j >= root[i,j]+1)
   print K {root[root[i,j]+1,j]} is the right child of K {root[i,j]}
   print-BST(root,root[i,j]+1,j)
else
   print d {j} is the right child of k {root[i,j]}

实际代码

#include<stdio.h>
#include<string.h>

#define N 5
#define MAX_FLOAT 10.0

void OPTIMAL_BEST(float* p, float* q, int n);
void CONSTRUCT_OPTIMAL_BST(int root[N + 1][N + 1]);
void Print_BST(int root[N + 1][N + 1], int i, int j);

void main() {
	float p[N + 1] = { 0.0,0.15,0.10,0.05,0.10,0.20 };
	float q[N + 1] = { 0.05,0.10,0.05,0.05,0.05,0.10 };
	OPTIMAL_BEST(p, q, N);

}
void OPTIMAL_BEST(float* p, float* q, int n) {
	float e[N + 2][N + 1];
	float w[N + 2][N + 1];
	int root[N + 1][N + 1];
	memset(e, 0.0, sizeof(float) * (N + 2) * (N + 1));
	memset(w, 0.0, sizeof(float) * (N + 2) * (N + 1));
	memset(root, 0, sizeof(int) * (N + 1) * (N + 1));
	for (int i = 1; i <= n + 1; i++) {
		e[i][i - 1] = q[i - 1];
		w[i][i - 1] = q[i - 1];
	}
	for (int l = 1; l <= n; l++) {
		for (int i = 1; i <= n - l + 1; i++) {
			int j = i + l - 1;
			e[i][j] = MAX_FLOAT;
			w[i][j] = w[i][j - 1] + p[j] + q[j];
			for (int r = i; r <= j; r++) {
				float t = e[i][r - 1] + e[r + 1][j] + w[i][j];
				if (t < e[i][j]){
					e[i][j] = t;
					root[i][j] = r;
				}
			}
		}
	}
	for (int i = 1; i <= n + 1; i++) {
		for (int j = 0; j <= n; j++) {
			printf("%.2f	", e[i][j]);
		}
		printf("\n");
	}
	printf("\n");
	printf("\n");
	printf("\n");
	for (int i = 1; i <= n + 1; i++) {
		for (int j = 0; j <= n; j++) {
			printf("%.2f	", w[i][j]);
		}
		printf("\n");
	}
	printf("\n");
	printf("\n");
	printf("\n");
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			printf("%d	", root[i][j]);
		}
		printf("\n");
	}
	printf("\n");
	printf("\n");
	printf("\n");
	CONSTRUCT_OPTIMAL_BST(root);
}

void CONSTRUCT_OPTIMAL_BST(int root[N + 1][N + 1]) {
	printf("K %d is the root\n", root[1][N]);
	Print_BST(root, 1, N);
}

void Print_BST(int root[N + 1][N + 1], int i, int j) {
	if (i <= (root[i][j] - 1)) {
		printf("k %d is the left child of k %d\n", root[i][root[i][j] - 1], root[i][j]);
		Print_BST(root, i, root[i][j] - 1);
	}
	else {
		printf("d %d is the left child of k %d\n", root[i][j] - 1, root[i][j]);
	}
	if (j >= root[i][j] + 1) {
		printf("k %d is the rightchild of k %d\n", root[root[i][j] + 1][j], root[i][j]);
		Print_BST(root, root[i][j] + 1, j);
	}
	else {
		printf("d %d is the right child of k %d\n", j, root[i][j]);
	}
}

15.5-2

Determine the cost and structure of an optimal binary search tree for a set of n = 7 keys with the following probabilities:

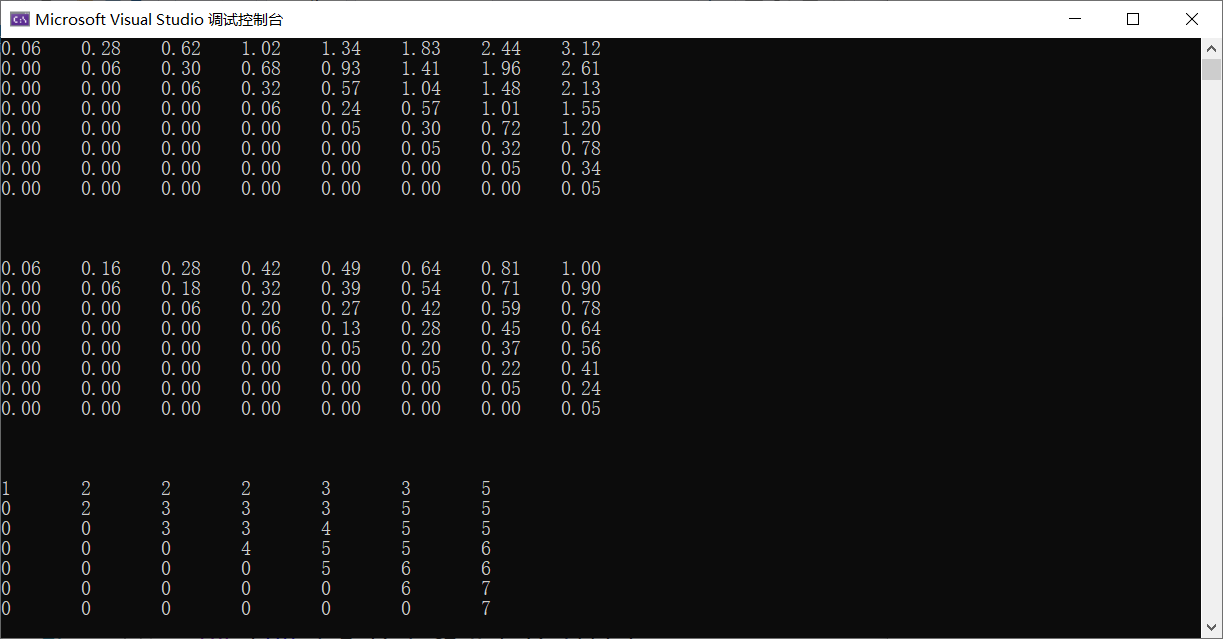
15.5-3

Suppose that instead of maintaining the table w[i, j], we computed the value of w(i, j) directly from equation (15.12) in line 9 of OPTIMAL-BST and used this computed value in line 11. How would this change affect the asymptotic running time of OPTIMAL-BST?

计算一个w(i,j)需要进行 (j - i +1 + j - i + 2 + 1 = j - i + 4)次加法。
而 j = i + l - 1，故而每次OPTIMAL-BST将计算(l - 1 + 4 = l + 3)次加法，那么该算法的时间复杂度为：O(n * n * (l+3)) + O(n * n * n) = O(n³)。
对于算法的渐进分析并没有什么影响，只是增加了一个常数，而常数在渐进分析中一般可忽略。

15.5-4

Knuth [212] has shown that there are always roots of optimal subtrees such that root[i, j] + 1 <= root[i, j] <= root[i + 1, j ] for all 1 <= i < j <= n. Use this fact to modify the OPTIMAL-BST procedure to run in (n²) time.

伪代码

空间结构：
M[1:n+1; 0:n]: 存储优化解搜索代价
W[1: n+1; 0:n]: 存储代价增量Wm(i, j)
Root[1:n; 1:n]: root(i, j)记录子问题{ki, …, kj}优化解的根

Optimal-BST(p, q, n)
 For  i=1  To  n+1   Do
      E(i, i-1) = qi-1;
      W(i, i-1) = qi-1;
 For  l=1  To  n   Do
      For   i=1   To   n-l+1   Do
            j=i+l-1;            
            E(i, j)=正无穷;
            W(i, j)=W(i, j-1)+pj+qj;
            // 这里对于l == 1的情况需要特殊处理，否则会造成数组越界
            if (l == 1){
                For  r=i  To  j   Do
                    t=E(i, r-1)+E(r+1, j)+W(i, j);
                    If    t<E(i, j)
                    Then  E(i, j)=t; 
                          Root(i, j)=r;
                continue;
            }
            For  r=Root[i-1,j]  To  Root[i,j+1]   Do
                 t=E(i, r-1)+E(r+1, j)+W(i, j);
                 If    t<E(i, j)
                 Then  E(i, j)=t; 
                       Root(i, j)=r;
 Return  E and  Root

代码将不会给出，只需要对15.5-1中代码作些许修改就可以

关于算法时间复杂度的分析：

这里是对于题目中knuth所给公式的证明，不过个人暂未观看

First prove this fact. Consider the optimal BST T[i+1,j] which has nodes from i+1 to j. Inserting a i node to T(i.e. i as i+1's left child, and proper adjustment to dummy nodes) makes also a legal BST T'[i,j]. If i+1's height is h, adding a i node leads to an increase of search cost by (h+1)p[i]+(h+2)q[i-1]+q[i]. When constructing the optimal BST T[i,j], if root[i,j] > root[i+1,j], then root[i+1,j] (in T[i,j]) must appear in the root[i,j]'s left subtree. Since i+1's depth, with respective to root[i+1,j] in T[i,j] is identical to that in T[i+1,j]. The actual i's depth, i.e. with respective to T[i,j]'s root, root[i,j], is thus larger. But, we have another optimal tree T[i,j], which as a less increasing cost when inserting node i. Thus, T[i+1,j] plus node i-1 can make a better tree, which contradicts T[i,j]'s optimism. Therefore, root[i,j]<=root[i+1,j]. Similarly, root[i,j-1]<=root[i,j].

某大佬题解

Thus, we can modify the formula to e[i,j] = min{,e[i,r-1]+e[r+1,j]+w(i,j)}, root[i,j-1]<=r<=root[i+1,j] .

Then we're to prove that the calculating of this formula, using dynamic programming, takes Θ(n^2) time. we call the group of states e[i,j] with the fixed j - i ( = k ) the level-k group(obviously there're n-k nodes in the group).the calculation of e[i,j] takes root[i+1,j] - root[i,j-1] + 1 iterations. thus, for all level-k group states, their calculations takes root[k,1] - root[1,k] + n - k(个人不理解为什么会这样) iterations in all. Since 1 <= root[k,1] , root[1,k] <= n, the number of iterations is thus Θ(n).nd the k varies from 0 to n-1. Thus the overall complexity is Θ(n)*n = Θ(n^2). This is a common trick to optimize a Θ(n^3) dp algorithm for some kind of problems into a Θ(n^2) one.

显然，在算法第5行循环的每次迭代中，i，j，l都是被固定的，迭代标志为l，那么，我们以k= l-1 唯一的标识算法第5行的循环的一次迭代，称其为 k-迭代。
第5行的循环的k-迭代需要处理 n-k 个e[i.j]，即:{ e[1,1+k], e[2,2+k], .., e[n-k , n]}。
每个e[i,j]将会使得第10行循环进行 root[i+1,j] - root[i,j-1] + 1次。
在第5行循环的k-迭代过程中，第10行的迭代次数总和为

\[\begin{equation} \begin{aligned} & root[2,1+k]-root[1,k]+root[3,2+k]-root[2,1+k]+\cdots+root[n-k+1,n]-root[n-k,n-1] + n-k\\ = & root[n-k+1,n] - root[1,k]+n-k\\ = & Θ(n) \end{aligned} \end{equation} \]

Ps:

\[\begin{equation} \begin{aligned} & root[n-k+1,n] \le n,root[1,k]\ge 1\\ & root[n-k+1,n] - root[1,k] \le n-1 \end{aligned} \end{equation} \]

那么，第5行循环一共迭代n次，k = < 0, 1 ,..., n-1 >
总时间复杂度为Θ(n²)

15-1 Longest simple path in a directed acyclic graph

Suppose that we are given a directed acyclic graph G = (V, E) with realvalued edge weights and two distinguished vertices s and t . Describe a dynamicprogramming approach for finding a longest weighted simple path from s to t . What does the subproblem graph look like? What is the efficiency of your algorithm?

15-2 Longest palindrome subsequence

A palindrome is a nonempty string over some alphabet that reads the same forward and backward. Examples of palindromes are all strings of length 1, civic, racecar,and aibohphobia (fear of palindromes). Give an efficient algorithm to find the longest palindrome that is a subsequence of a given input string. For example, given the input character, your algorithm should return carac. What is the running time of your algorithm?

针对这个问题，完全可以使用LCS最长公共子序列问题的算法进行求解，将所给字符串A进行倒置得到字符串B，计算A，B的最长公共子序列即可。

至于直接解决该问题的动态规划算法，可以参见本人博客。

15-3 Bitonic euclidean traveling-salesman problem

In the euclidean traveling-salesman problem, we are given a set of n points in the plane, and we wish to find the shortest closed tour that connects all n points.

Figure (a) shows the solution to a 7-point problem.

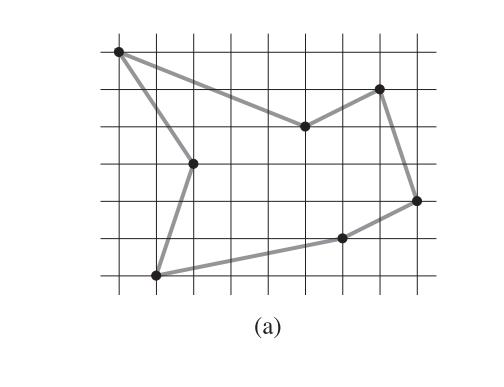
The general problem is NP-hard, and its solution is therefore believed to require more than polynomial time (see Chapter 34).

J. L. Bentley has suggested that we simplify the problem by restricting our attention to bitonic tours, that is, tours that start at the leftmost point, go strictly rightward to the rightmost point, and then go strictly leftward back to the starting point.

Figure (b) shows the shortest bitonic tour of the same 7 points.

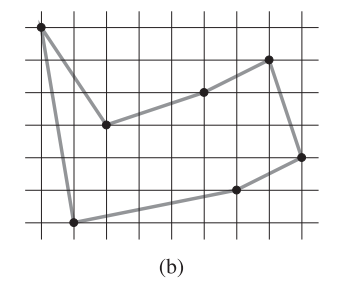
In this case, a polynomial-time algorithm is possible. Describe an O(n²) time algorithm for determining an optimal bitonic tour.

You may assume that no two points have the same x-coordinate and that all operations on real numbers take unit time.

(Hint: Scan left to right, maintaining optimal possibilities for the two parts of the tour.)

posted @ 2020-10-13 19:53 zqybegin 阅读(3550) 评论(0) 编辑收藏举报

刷新页面返回顶部

		0	1	2	3	4	5	6	7	8
			`1`	`0`	`0`	`1`	`0`	`1`	`0`	`1`
0		0	0	`0`	0	0	0	0	0	0
2	`0`	`0`	0	1	`1`	1	1	1	1	1
3	`1`	0	`1`	1	1	`2`	2	2	2	2
4	`0`	0	1	`2`	2	2	`3`	3	3	3
5	`1`	0	1	`2`	`2`	3	`3`	4	4	4
6	`1`	0	1	`2`	2	`3`	3	`4`	4	5
7	`0`	0	1	2	`3`	3	`4`	4	`5`	5
8	`1`	0	1	2	3	`4`	`4`	5	`5`	6
9	`1`	0	1	2	3	4	4	`5`	5	`6`
10	`0`	0	1	2	3	4	5	5	`6`	`6`

		0	1	2	3	4	5	6	7	8
			`1`	`0`	`0`	`1`	`0`	`1`	`0`	`1`
0		0	0	`0`	0	0	0	0	0	0
2	`0`	`0`	0	1	`1`	1	1	1	1	1
3	`1`	0	`1`	1	1	`2`	2	2	2	2
4	`0`	0	1	`2`	2	2	`3`	3	3	3
5	`1`	0	1	`2`	`2`	3	`3`	4	4	4
6	`1`	0	1	`2`	2	`3`	3	`4`	4	5
7	`0`	0	1	2	`3`	3	`4`	4	`5`	5
8	`1`	0	1	2	3	`4`	`4`	5	`5`	6
9	`1`	0	1	2	3	4	4	`5`	5	`6`
10	`0`	0	1	2	3	4	5	5	`6`	`6`

zqybegin

算法导论15章答案

15.1-1

15.1-2

15.1-3

15.1-4

15.1-5

15.2-2

15.2-3 未完成

15.2-4

15.2-5

15.2.6

15.3-1 疑问

15.3-2

15.3-3

15.3-4

15.3-5

15.3-6 未完成

15.4-1

15.4-2

15.4-3

15.4-4

15.4-5 未完成

15.4-6 未完成

15.5-1

15.5-2

15.5-3

15.5-4

15-1 Longest simple path in a directed acyclic graph

15-2 Longest palindrome subsequence

15-3 Bitonic euclidean traveling-salesman problem

公告

		0	1	2	3	4	5	6	7	8
			`1`	`0`	`0`	`1`	`0`	`1`	`0`	`1`
0		0	0	`0`	0	0	0	0	0	0
2	`0`	`0`	0	1	`1`	1	1	1	1	1
3	`1`	0	`1`	1	1	`2`	2	2	2	2
4	`0`	0	1	`2`	2	2	`3`	3	3	3
5	`1`	0	1	`2`	`2`	3	`3`	4	4	4
6	`1`	0	1	`2`	2	`3`	3	`4`	4	5
7	`0`	0	1	2	`3`	3	`4`	4	`5`	5
8	`1`	0	1	2	3	`4`	`4`	5	`5`	6
9	`1`	0	1	2	3	4	4	`5`	5	`6`
10	`0`	0	1	2	3	4	5	5	`6`	`6`