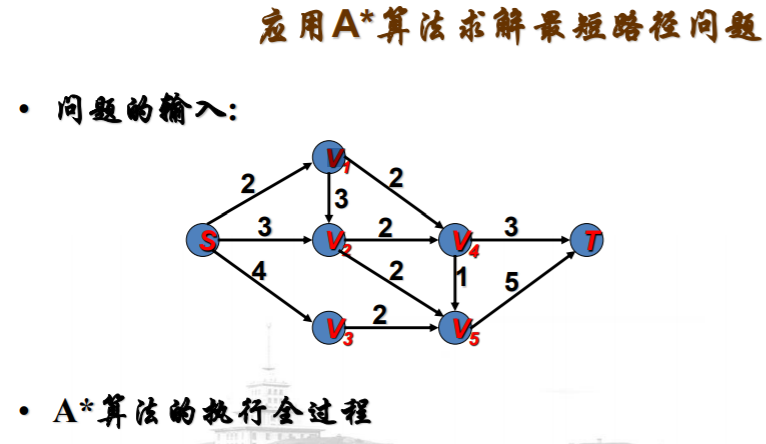
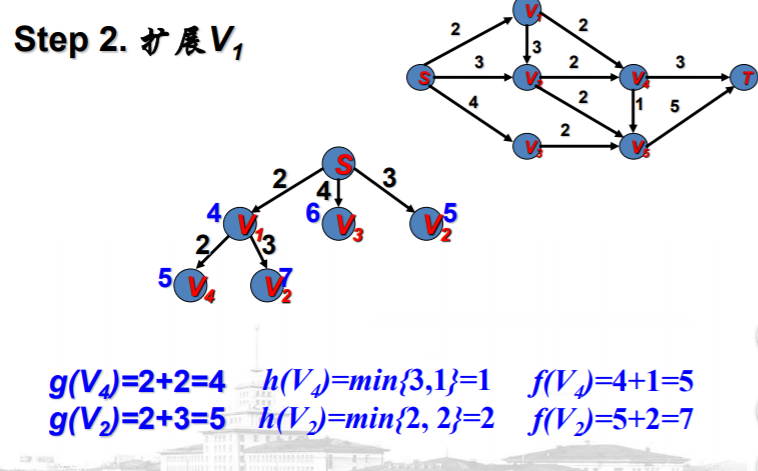
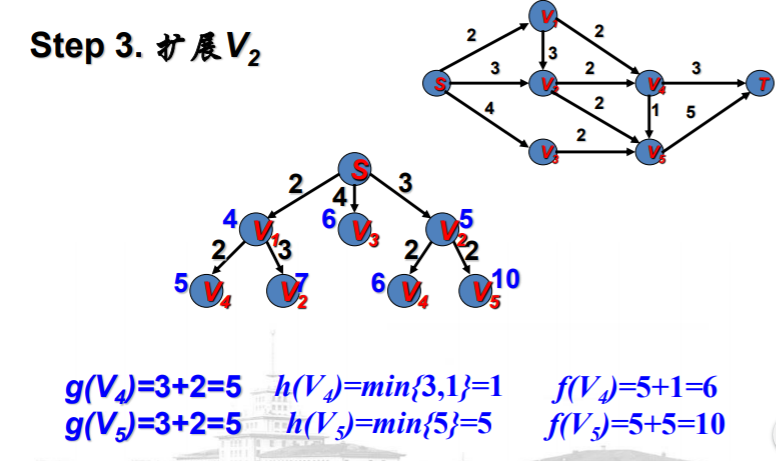
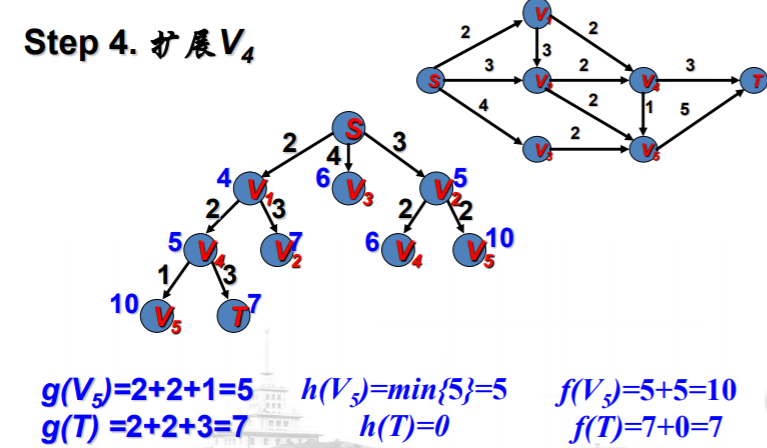
A*算法的有关知识--例子:最短路径问题
前置知识
定义1,g(n)=从树根到节点n的代价。当算法处理到某个节点时,g(n)是可以精确计算的。
定义2,h*(n)=从节点n到目标节点的优化路径的代价。一般不可知。
定义3,f*(n)=g(n) + h*(n)是包含节点n的路径的最小代价。一般不可知。
定义4,h(n)=从节点n到目标节点的优化路径的估计代价。
定义5,f(n)=g(n) + h(n)是包含节点n的路径的估计最小代价。
假设,对于任意的节点n而言,已知h*(n),可以构建出一个算法直接找到最优解,即处理每一次选择时,都选择f*(n)代价最小的节点。但是,对于任意一个算法而言,h*(n)不可知,我们只能够估计h*(n)的值,这也是爬山法和Best-Frist算法中评价函数或启发式函数的作用。
算法本质
A*算法保证所估计h*(n)的值h(n)满足:h(n) ≤ h*(n)。
一旦满足这个条件,当使用使用Best-first策略搜索时,如果该方法选中的节点是目标节点,那么该节点表示的解就是当前问题的最优解。
定理1,使用Best-first策略搜索,且满足h(n) ≤ h*(n),如果算法选择的节点是目标节点, 则该节点表示的解是优化解。
证明1:只需要证明,f*(t)是最优解代价即可,n为此时可以进行扩展的所有节点,即f*(t)是{f*(n)}中的最小值。
- 由于节点t是目标节点,所以h*(t) = h(t) = 0,f(t) = f*(t) = g(t)。
- 假设:{f*(n)}中的最小值为M,M∈{f*(n)}。
- 由于 f*(t)∈{f*(n)},故而,f(t) ≥ M。
- 由于此时算法选择的节点是节点t,即在当前可以扩展的节点中,t是估计总代价最小的那一个,故而 f(t) ≤ f(n) ,而对于所有当前可以扩展的节点n而言,由于h(n) ≤ h*(n),所以 f(n) ≤ f*(n),而{f*(n)}中的最小值为M,f(t) ≤ M。
- 由 f(t) ≥ M 以及 f(t) ≤ M 可知,f(t) = M。
算法拓展
可以将A*算法的h(n)作两种极端情况的考虑。
- 对于任意的节点n,h(n) = 0,此时算法退化,每一次进行选择时,选择当前g(n)最小也就是当前路径长度最小的点。
- 对于任意的节点n,h*(n) = 0,正如本文之前提到的,直接可以选择得到,不会走其他路径。
由此,可以明确的是,尽量使得h(n)接近h*(n),越接近,算法越佳。
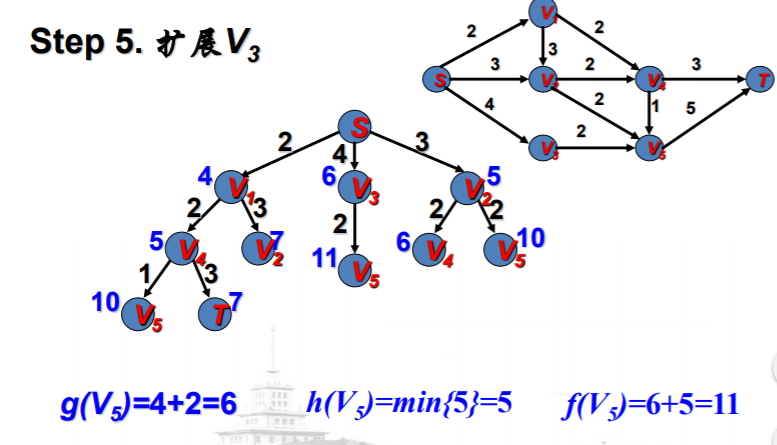
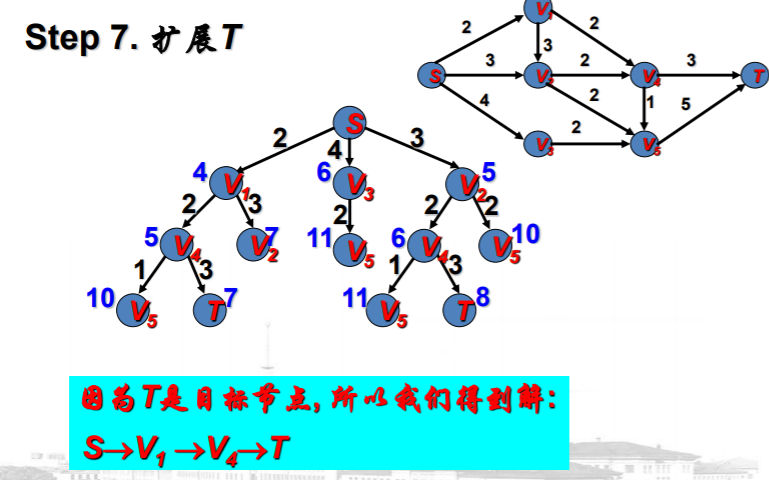
例子说明