旅行商问题--搜索算法求解
问题定义
输入
- 连通图G = (V,E),每个节点都没有到自身的边,每对节点之间都有一条非负加权边。
输出
- 一条由任意一个节点开始,经过每个节点一次,最后返回开始节点的路径
- 该路径的代价(即路径中所有边的权值之和)最小
搜索策略
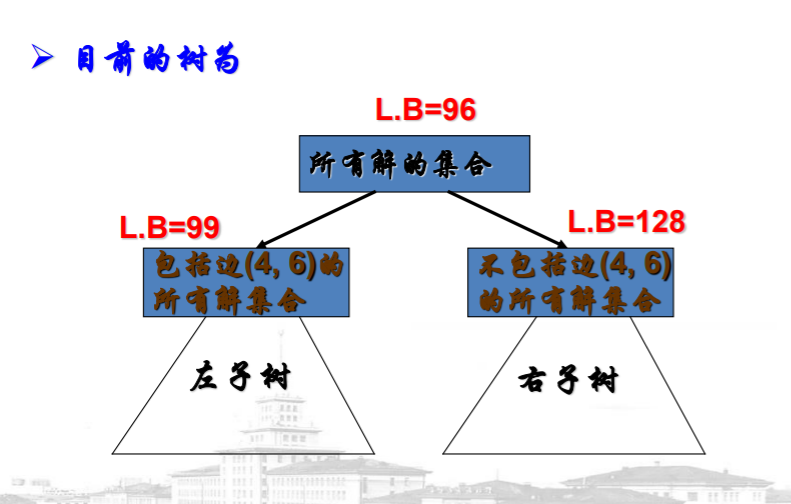
- 构建一颗二叉树,其每个节点代表部分解空间,树根代表所有解的集合。
- 一个节点的左右子节点表示,对于该节点代表解空间A的一个划分,划分依据一般为某条边C,左子节点代表:解空间A中包含该边C的所有解,右子节点代表:解空间A中不包含该边C的所有解。
- 不断的扩展节点,使用爬山法的思想,先扩展左子树中可能权值下界尽可能低的节点,得到一个权值较低的可行解。而后处理所有节点,在这一过程中,可以剪去一定不可能产生最优解的分支以及更新权值下界。
- 当需要扩展某一结点采用下述办法:
- 采用人员安排问题的搜索策略中的技巧1,对当前的权值矩阵进行化简,同时计算当前节点所代表解空间的权值下界。
- 在当前权值矩阵中,在所有权值为0的点中,选取该点所在的行以及列的最小值之和最大的点。以该点所代表的边作为子节点的划分依据。
- 计算子节点的权值。
左子节点代表的解空间的权值下界 = 父节点的权值下界 + 作为划分依据的边的权值。
右子节点代表的解空间的权值下界=父节点的权值下界+作为划分依据的边在权值矩阵中所在行与列的最小值之和
- 同时需要更新左右子节点的权值矩阵。对于左节点而言,删去父节点权值矩阵中作为划分依据点所在的边以及列,同时,置与该节点横纵坐标相反的节点的权值为无穷。对于右节点而言,置父节点权值矩阵中作为划分依据点的权值为无穷。
对于搜索策略中某些疑问的解释
- 在本例中使用二叉树来处理搜索,而不是采用一般的从某个节点的选择为扩展方向的树,目的就是方便于剪支,使得当判断不可能时,尽可能剪去较多的解空间。
- 选择划分依据点的操作的理论基础。该算法会首先扩展左子树,以期获得一个下界较高的可行解,通过该解的下界进行剪支。为了剪支更好地进行,可以使得左节点的下界尽可能的低,而右节点的下界尽可能的高,这样,一旦在左子树找到某个可行解,进行剪支时,可能剪去的部分会较多。对应于操作之中,则选择权值较小的点使得左节点的下界尽可能的低,选择该点的行以及列的最小值之和最大,则是为了尽可能提高右节点的下界。而,之所以取划分点的行以及列的最小值之和,是因为右子树不包含(i,j)这条边,但是,其一定存在一条从顶点i出发的一条边以及进入顶点j的一条边,取行列最小值之和是为了估计右节点代表解空间的下界。
- 处理左右子节点的权值矩阵的理论基础。之所以要对左子节点做出如此处理,是因为该问题的定义中,明确只能经过某点一次,也就是说,在图中的任一顶点,都只能有入以及出的边,而左子节点代表的解都包含(i,j)边,故而,所有i出的边以及j入的边都不可能,故而删去。另外,至于将“与该节点横纵坐标相反的节点的权值为无穷”这一操作,一般而言,旅行商问题的G的顶点数都会大于2,这就要求了不可能存在两个点之间由两条边直接构成圈,否则,这两个点将不会与其他点之间存在边,无法构成可行解。至于对于右子节点的权值矩阵的处理,较为简单,右子节点表示不包含(i,j)边,自然将之置为无穷即可。
例子
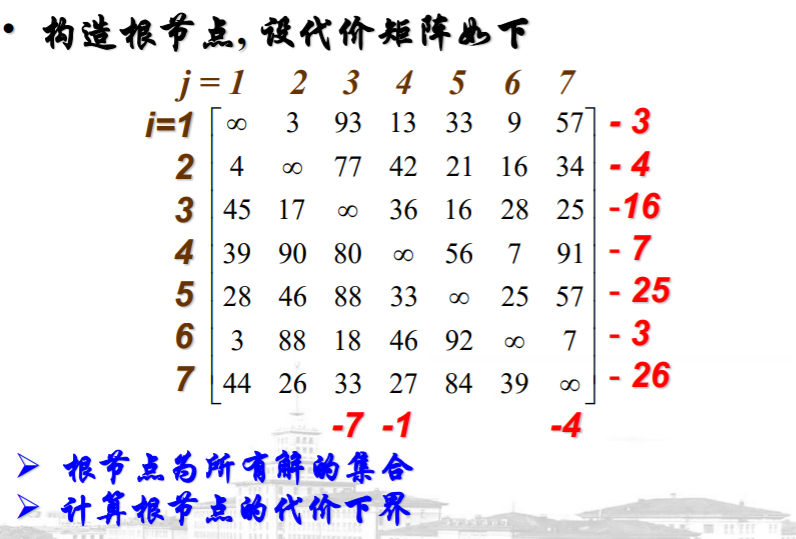

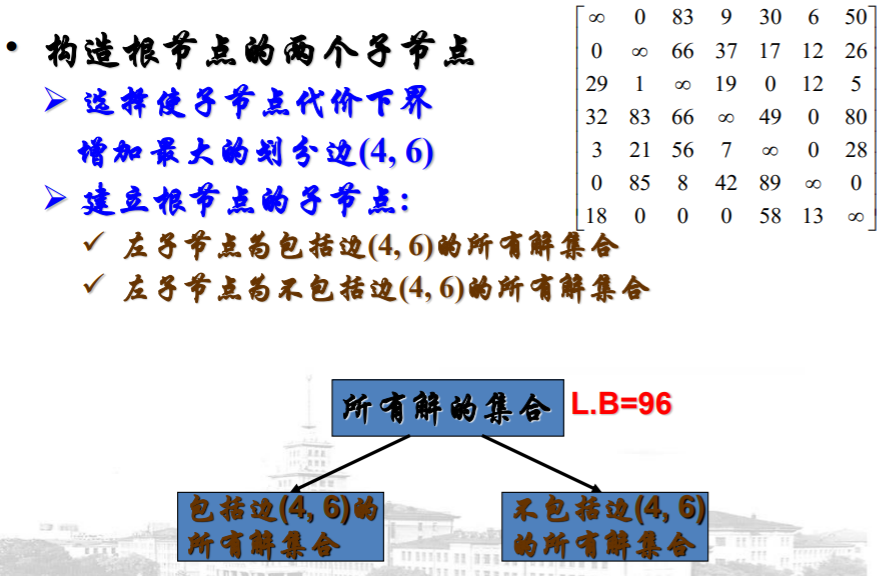



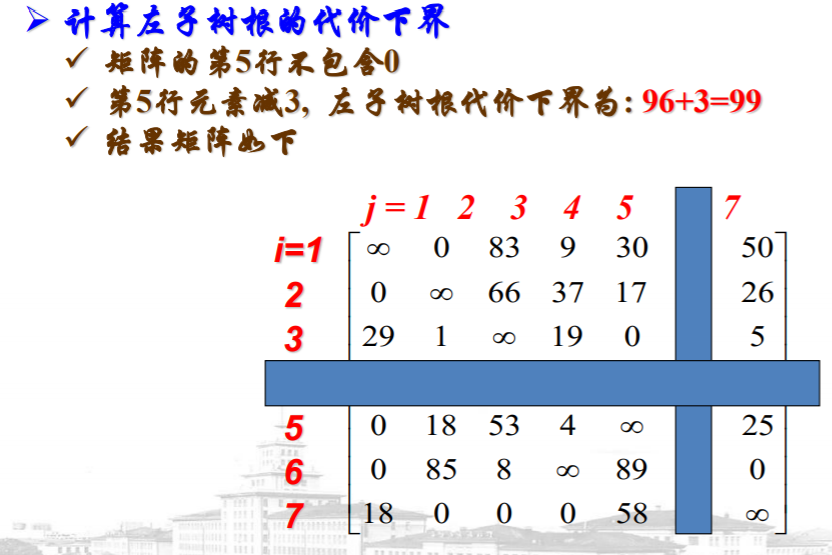

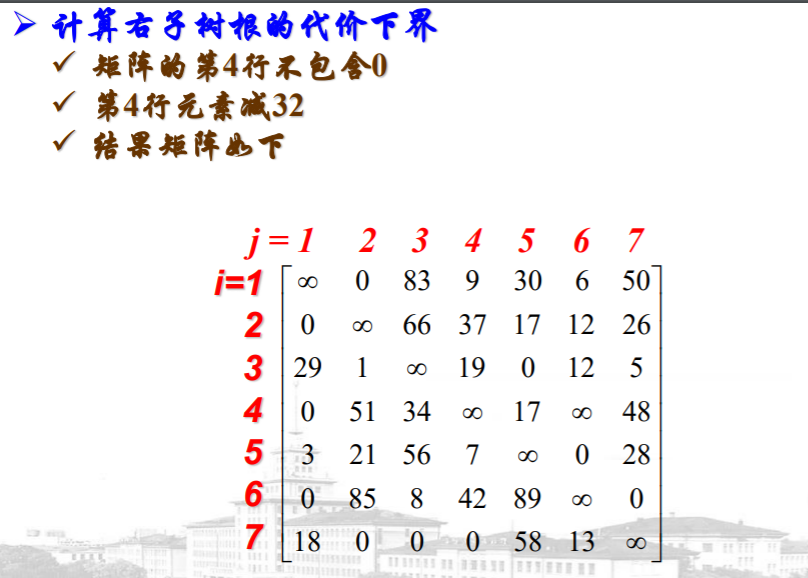





 浙公网安备 33010602011771号
浙公网安备 33010602011771号