最小生成树算法
问题描述:
生成树:在一个任意连通图G中,如果取它的全部顶点和一部分边构成一个子图G',即:V(G')=V(G)和(G')⊆E(G)。若子图G'同时满足边集E(G')中的所有边既能够使全部顶点连通而又不形成任何回路,则称子图G'是原图G的一棵生成树。
一个任意连通图G=(V,E)的生成树G'=(V,E’),那么 |E'| = |V| - 1。
要证明这一特点有许多角度,例如:
- 树的每一个结点都有一个唯一的父亲,也就是至少有n条边,但是根节点要除外,所以就是n-1条边。
- 树里不存在环,那么既要连接n个点又不能形成环,只能用n-1条边。
加权连通图G的最小生成树:在所有的G的生成树T中,使得边的权值之和最小的生成树。
输入:无向连通图G=(V, E), 权函数W
输出:G的最小生成树
Kruskal()算法与Prim()算法的差别以及联系:
Kruskal()算法与Prim()算法都是每次选取最小的边,不过Kruskal()算法是满足条件的边,而Prim()算法选取点,依次选取离当前点集合最近的点。
算法1:Kruskal()算法
算法描述:
1. 确定贪心思想
其实求G的最小生成树就是求最小生成树的边集,依照下述思想构建最小生成树的边集S:
- 删除E中可以与S中边构成圈的所有边。
- 取E中权值最小边,并将其加入到S中,在E中删除该边。
- 重复进行上述两步操作,直到E为空集。
2. 分析贪心选择性。
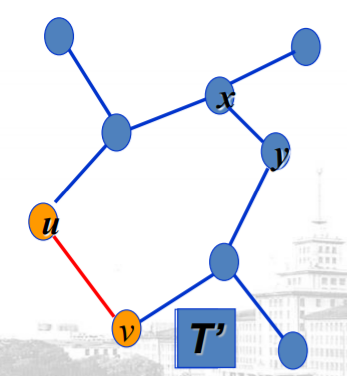
引理1:设uv是G中权值最小的边,则必有一棵G的最小生成树包含边uv。
证明:如果不存在这样的一个最小生成树,那么可以设:设T是G的的某棵最小生成树,且uv不在T中,那么,在T中添加uv边,产生环,删除环中不同于uv的任意边xy,得到T '。w(T ')=w(T ) - w(xy) + w(uv) ≤ w(T),而T是G的的某棵最小生成树,矛盾,假设不成立。
3.分析优化子结构
定义1:收缩图G的边uv,即用新顶点C代替顶点u,v,同时,将G中原来与u或v关联的边与C关联,删除C到其自身的边。记作G·uv。而将上述操作的逆操作称为扩张,记作G.uv。
定义2:任意树的权值记为W(T),W(T) = ∑ (u,v)∈VW(u,v),W(i,j)是边ij的权值。
引理2:给定加权无向连通图G=(V,E),权值函数为 W:E→R, uv是G中权值最小的边。设T是G的最小生成树,那么T·uv就是图G·uv的最小生成树。
证明:如果G.uv不是图G.uv的最小生成树。那么一定存在树M是G.uv的最小生成树,那么W(M.uv) = W(M) + W(u,v),而W(T) = W(T·uv) + W(u,v)。而W(T·uv) > W(M),故而W(T) > W(M.uv)。这与T是G的最小生成树矛盾,故而假设不成立。
4.分析算法正确性
其贪心选择性就是按照该算法思想构造解的数学归纳证明,使用引理1,引理2可以得到证明。此问题的解的构造不若任务安排问题可以进行很好的形式化,就不展开说明。
5.设计算法
根据贪心思想设计算法。
MST-Kruskal(G,W)
A = null;
For 任意的v属于V[G] Do
Make-Set(v); /*为每个点构建并查集*/
按照W值的递增顺序排序E[G];
For 任意(u, v)属于E[G] (按W值的递增顺序) Do
If Find-Set(u) != Find-Set(v)
/*u,v不在一个并查集中,说明此时构建的树中,二者之间不存在路*/
Then A=AU{(u, v)};
Union(u, v);
Return A
6.算法复杂性分析:
时间复杂性分析:
令 n=|V|, m=|E|,那么
第5行需要时间:O(mlogm)。
第3~4行执行 O(n) 个Make-Set操作。第6~10行执行O(m)个Find-Set和Union 操作。共需要时间O((n+m)α(n))。
而由于m ≥ n-1 (连通图),故而 α(n)=logn=logm。这里需要使用到并查集的平摊分析。
总的时间复杂度为 O(mlogm)。
算法2:Prim()算法
算法描述:
1. 确定贪心思想
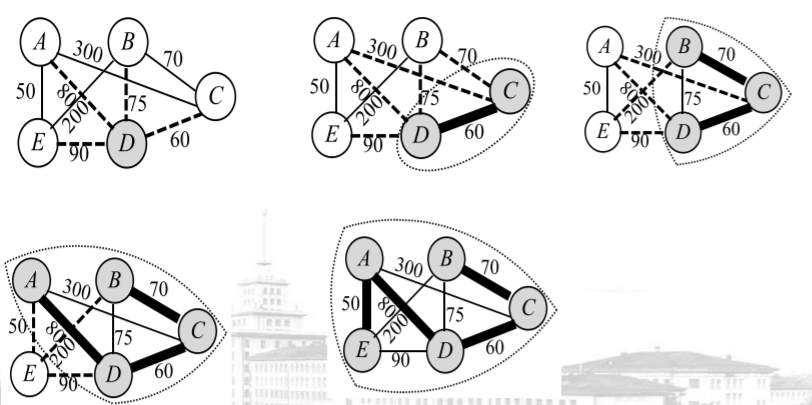
其实求G的最小生成树就是求最小生成树的边集,依照下述思想构建最小生成树的边集S:
- 构建点集M以及边集S,最初,M中含有图中任意一个点,S为null。
- 在E中与点集M相接的边中,选取权值最小的边加入到S中,且将该边的另一个顶点加入到M中。
- 重复进行上述两步操作,直到M = V。
2. 分析贪心选择性。
引理1:设uv是G中与顶点u关联的权值最小的边,u为任意顶点,则必有一棵G的最小生成树包含边uv
证明:如果不存在这样的一个最小生成树,那么可以设:T是G的的某棵最小生成树,且uv不在T中,那么,在T中添加uv边,产生环,删除环中不同于uv的任意边uv ',由于uv不在T中,故而一定存在uv 。得到T '。w(T ')=w(T ) - w(xy) + w(uv) ≤ w(T),而T是G的的某棵最小生成树,矛盾,假设不成立。

3.分析优化子结构
引理2:给定加权无向连通图G=(V,E),权值函数为 W:E→R, uv是G中与u关联的权值最小的边,u为任意顶点。设T是G的最小生成树,那么T·uv就是图G.uv的最小生成树。
证明:如果G·uv不是图G.uv的最小生成树。那么一定存在树M是G.uv的最小生成树,那么W(M.uv) = W(M) + W(u,v),而W(T) = W(T·uv) + W(u,v)。而W(T·uv) > W(M),故而W(T) > W(M.uv)。这与T是G的最小生成树矛盾,故而假设不成立。
4.分析算法正确性
其贪心选择性就是按照该算法思想构造解的数学归纳证明,使用引理1,引理2可以得到证明。此问题的解的构造不若任务安排问题可以进行很好的形式化,就不展开说明。
5.设计算法
根据贪心思想设计算法。
MST-Prim(G,W,r)
Input 连通图G,权值函数W,树根r
Output G的一棵以r为根的生成树
C = {r},T = null;
建堆Q维护C与V-C之间的边
While C != V do
uv=Extract_Min(Q) //u属于C,v不属于V-C
C = C U{v};
T = T U{uv};
for 任意的x属于Adj[v] do /*Adj[v]是与v之间存在边的顶点集*/
if x属于C then 将vx从Q中删除
Else 将vx插入Q
Return T
使用二叉最小堆来进行具体的撰写,我看不懂。
MST-Prim(G,W,r) Input 连通图G,权值函数W,树根r Output G的一棵以r为根的生成树 For 任意的v属于V[G] Do key[v] = 无穷; Π[v] = null; key[r] = 0; Q = V[G]; While Q != null do u = Extract_Min(Q); for 任意的v属于Adj[u] do /*Adj[v]是与v之间存在边的顶点集*/ if v属于Q 且 w(u,v)<key[v] then Π[v] = u; key[v] = w(u,v) //更新信息; Return A={(v, Π[v])| v 属于 V[G] -r}
6.算法复杂性分析:

对于该问题的拓展思考
- 将无向图改为有向图,同时定义有向图的最小生成树的每条边的方向都必须保持一致,即:要么全部边由父节点指向子节点,要么全部边由子节点指向父节点。
- 对于该问题而言,Kruskal()算法显然不适用,而对于Prim()算法的正确性分析,本文描述的算法证明对于选择正确性以及优化子结构都是不满足条件的,因为在这些证明中,都需要添加uv边而后删去某条边,在有向图中,该方法可能会改边子节点的指向,使得构造的树都不满足条件。
- 将最小生成树修改为最大生成树,感觉Kruskal()算法和Prim()算法的正确性证明都适用,只需要做略微修改。
- 对于最小生成树添加限制,限制其度不超过k。



