哈夫曼编码问题

问题描述

       前缀编码：无任何字符的编码是另一个字符编码的前缀。

 

        编码树的代价：

• 设C是字母表,任意的c属于C
• F(c)是c在文件中出现的频率
• D_T (c)是叶子c在树T中的深度，即c的编码长度
• T的代价是编码一个文件的所有字符的代码位数:   B(T)= ∑_c∈C F(c) D_T(c) 

       输入：字母表C = {c₁,c₂,...c_n},频率表F = {F(c₁),F(c₂),...,F(c_n)}

       输出：具有最小代价B(T)的前缀编码树T

算法描述

     1. 确定贪心思想

       循环地在节点集合中选择具有最低频率的两个结点， 生成一棵子树，将该子树再放入到节点集合中，直至形成树。

     2. 分析贪心选择性。

       引理1：设C是字母表，任意的c∈C，c具有频率F(c), x、y 是C中具有最小频率的两个字符，则存在一个C的优化前缀树，x与y的编码都具有最大的长度，而且存在一 个C的优化前缀树一定含有一个子树为x与y生成的子树。

       证明1：假设x的编码不具有最大的长度，那么，可以设设T是C的最优前缀树T，且b和c是具有最大深度的两个字符。T的简略图示如下：

 

       节点b，c中至少有一个点的频率要不小于x的频率，不失一般性，假设该点为节点b。则f(b) ≥ f(x)，可以构造构造T '，即交换树T中节点x和节点b的位置，其图示如下：

 

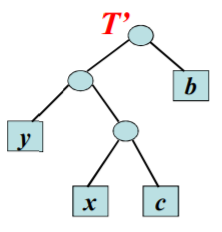
            B(T) - B(T ')

          =∑ F(c)D_T(c) - ∑ F(c)D_{T '}(c)

          =F(x)D_T(x) + F(b)D_T(b) - F(x)D_{T '}(x) - F(b)D_{T '}(b)

          =F(x)D_T(x) + F(b)D_T(b) - F(x)D_T(b) - F(b)D_T(x)

          =[ F(b) - F(x) ][ D_T(b) - D_T(x) ]  ≥ 0 

    即：B(T ) ≥ B(T ')

        那么，至少存在编码树T '使得其代价不小于当前的最优编码树，这与假设矛盾，故而x的编码具有最大的长度。

        同理，y的编码具有最大的长度。

        那么，在一棵编码树中，具有最大长度的节点深度相同，即这两个节点要么位于同一棵子树的左右两支，要么位于一个树的同一层，而对于这两个节点位于一个树的同一层，可以进行节点交换，使得它们位于同一棵树的两支，这并不会改变树的代价。

     3.分析优化子结构

       引理2：设T是字母表C的优化前缀树，任意的c∈C，F(c) 是c在文件中出现的频率.设x、y是T中任意两个相邻叶结点，z是它们的父结点，则z作为频率是F(z)=F(x)+F(y)的字符，T '= T- {x,y}是字母表C '=C-{x,y}∪{z}的优化前缀编码树.

       证明2：如果T '不是字母表C '=C-{x,y}∪{z}的优化前缀编码树。那么一定存在T ''，B(T '') < B(T ')。而后将x节点与y节点加入T ''中，作为z的左右子节点，那么就可以得到C的一个前缀编码树T '''，那么接下来分析T 以及T '''之间的代价关系，寻找矛盾。

       要分析T 以及T "'之间的代价关系，需要借助桥梁T '。

       首先证明：B(T)=B(T ')+F(x)+F(y)。

       证：任意的v∈C-{x,y}, dT(v)=dT'(v), f(v)dT(v)=f(v)dT’(v)

              而B(T)与B(T ')之间只是差距了节点z以及节点x，y。

              D_T(x)=D_T(y)=D_{T '}(z)+1。

             那么 F(x)D_T(x) + F(y)D_T(y)

                   =[ F(x) + F(y) ] * [D_{T '}(z)+1]

                   =F(z)D_{T '}(z) + F(x) + F(y)

             方程两边同时加任意的v∈C-{x,y}的代价。

             可得     B(T) = B(T ') + F(x) + F(y)

             同理     B(T '") =  B(T '') + F(x) + F(y)

             而         B(T ') > B(T '') ，因为T ''是最优解

             则         B(T '") < B(T) , 这与T是字母表C的最优前缀树矛盾，故而T '是字母表C '=C-{x,y}∪{z}的优化前缀编码树。

     4.分析算法正确性

       其贪心选择性就是按照该算法思想构造解的数学归纳证明，使用引理1，引理2可以得到证明。此问题的解的构造不若任务安排问题可以进行很好的形式化，就不展开说明。

     5.设计算法

        根据贪心思想设计算法。

Huffman(C，F)
n = |C|;
Q = C; /* 用BUILD-HEAP建立堆 */
FOR i=1 To n-1 Do
      z = Allocate-Node( );
      x = left[z] = Extract-MIN(Q); /* 堆操作*/
      y = right[z] = Extract-MIN(Q); /* 堆操作*/
      f(z) = f(x)+f(y);
      Insert(Q, z); /* 堆操作*/
Return

　　

　6.算法复杂性分析：

       时间复杂性： 第3步的堆排序的BUILD-HEAP建立，其时间复杂性为O(n)。

                              第4步的循环中的堆操作为O(logn),共循环n-1次，时间复杂性为O(nlogn)。

                              时间复杂性T(n) =  O(n) + O(nlogn) = O(nlogn) 。