牛客D-Where are you /// kruskal+tarjan找无向图内的环

题目大意：

https://ac.nowcoder.com/acm/contest/272/D

在一个无向图中，给定一个起点，从起点开始走遍图中所有点

每条边有边权wi，表示第一次经过该道路时的花费（第二次及以后经过时花费为0）

此时用最少花费完成可能存在多种方案

求每种方案都必须经过的边有多少条

 

首先想到最小生成树

然后想到在得到最短边时 若存在其他长度相等的边 这条边此时就可被替代

但如果没有长度相等的边 那么这条边就是必须经过的边

然而这个想法经不起考验 是错误的 如下

 

但是没有长度相等的边 就是必须经过的边 这是毋庸置疑的

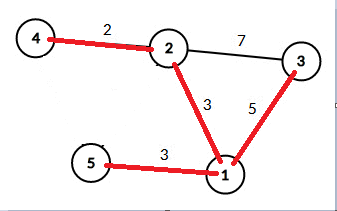
那么再观察下图

 

可以看到这是 一个只由长度相等的边组成的图

若在这个图中 我们要得到一棵生成树的话 边3-4是必选的 而剩下的1-2、2-3、3-1则任选两条即可

也就是说在生成树的所有选择方案里 这三条边不是必须经过的边

那么可以发现 在一个只由长度相等的边组成的图内 能形成一个环的几条边不是在所有的选择方案里必须经过的边

 

再结合kruskal得到最小生成树的步骤 每次先得到所有相同长度的最短边建图

再找到其中的环的个数m 那么要连接所有的环 必须经过的边就有m-1条

 

tarjan 求无向图内的环 就是在 有向图求强联通分量 的基础上进行修改

将 已走过的边 视为有向 不走其反向边

那么当走完这个图之后 整个图变成了一个有向图 此时图中的强联通分量就是环

 

如何 将已走过的边视为有向 呢

首先建图的过程中 对于一条边 我们是连了正向就连反向的 也就是这两条有向边在存储过程中的序号是连续的

所以我们从序号2开始存边的话 序号为 2和3 的两条有向边对应一条无向边 4和5对应一条无向边 6和7对应一条......

则对于 存储顺序为第 x 的有向边 其对应的反向边（即另一条有向边）顺序为 (x^1)

那么我们在递归时将上一条边的顺序 last 作为参数传过来 不走它对应的反向边即跳过顺序为 last^1 的边 就可以了

 

#include <bits/stdc++.h>
#define mem(i,j) memset(i,j,sizeof(i))
using namespace std;
const int N=2e5+5;
 
struct EDGE {
    int u,v,w;
    bool operator <(const EDGE& p)const {
        return w<p.w;
    }
}E[N<<1];
struct NODE { int to,nt; }e[N<<1];
int head[N], tot;
void addE(int u,int v) {
    e[++tot].to=v;
    e[tot].nt=head[u];
    head[u]=tot;
}
int dfn[N], low[N], ind;
int fa[N], ans;
int n, m, p;
void init_e() {
    ind=0; mem(dfn,0);
    tot=1; mem(head,0);
}
void init_s() {
    ans=0;
    for(int i=1;i<=n;i++) fa[i]=i;
}
 
int tarjan(int u,int last) {
    dfn[u]=low[u]=++ind;
    int res=0;
    for(int i=head[u];i;i=e[i].nt) {
        if(i==(last^1)) continue; // 是上一条边的对应反向边 跳过
        int v=e[i].to;
        if(!dfn[v]) {
            res+=tarjan(v,i);
            low[u]=min(low[u],low[v]);
        } else low[u]=min(low[u],dfn[v]); 
    }
    if(dfn[u]==low[u]) res++;
    return res;
}
 
int getfa(int x) {
    if(x==fa[x]) return x;
    return fa[x]=getfa(fa[x]);
}
void unite(int x,int y) {
    x=getfa(x), y=getfa(y);
    if(x!=y) fa[x]=y;
}
 
void Kruskal() {
    sort(E,E+m);
    for(int i=0,j;i<m;i=j) {
        j=i;
        while(j<m && E[j].w==E[i].w) j++; //找到所有与最短边相等的边
        init_e(); // 初始化邻接表和tarjan需要的数组
        for(int k=i;k<j;k++) { // 建图
            int u=getfa(E[k].u), v=getfa(E[k].v);
            if(u==v) continue; // 两个点已经连起来了
            addE(u,v); addE(v,u);
        }
        for(int k=i;k<j;k++) {
            int u=getfa(E[k].u);
            if(!dfn[u]) ans+=tarjan(u,0)-1; //保证m个环连通 需要m-1条边
        }
        for(int k=i;k<j;k++)
            unite(E[k].u,E[k].v);
    }
}
 
int main()
{
    while(~scanf("%d%d%d",&n,&m,&p)) {
        init_s();
        for(int i=0;i<m;i++)
            scanf("%d%d%d",&E[i].u,&E[i].v,&E[i].w);
        Kruskal();
        printf("%d\n",ans);
    }
 
    return 0;
}