数据结构-图
1.图的概念
-
基础概念
-
顶点集合(vex-set):如上图 S(vex) =
-
边集合(arc-set):如上图 S(arc) =
-
度(degree):⽆向图中从⼀个点延伸出去的边数就是该点的度;有向图中包含出度和⼊度;
- 出度(out-degree):有多少条边指向某点就是该点的出度;
- ⼊度(in-degree):从某点出发向外指向延伸的边数就是该点的⼊度;
-
-
图的分类:有向图,无向图,权重图
- 有向图
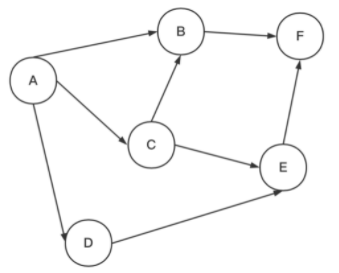
- 无向图
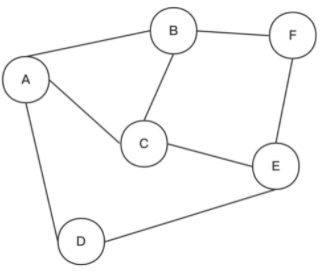
- 权重图
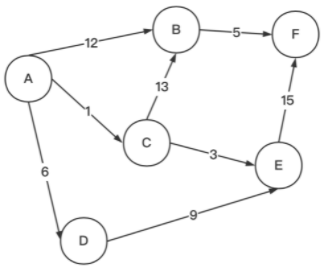
- 有向图
-
图的储存
-
存储的关键是点集合和边集合;
-
使用邻接矩阵储存:顶点信息存储在⼀维数组中,边信息存储在⼆维数组中(不常用)
- 优点和缺点
- 优点:很容易算出边邻接关系;以及节点的度(不管是出度还是⼊度)
- 缺点:边集合存储空间复杂度⽐较⼤,图中⼤量0,空间利⽤率不⾼(尤其在点多边少的情况下);对于⽆向图,邻接矩阵是对称的,可以只存下半部分。
- 优点和缺点
-
使用连接表储存(常用):顶点集合依然存储在⼀维数组当中,边集合存储在连接表当中;
- 优点和缺点:
- 优点:很容易算出邻接关系;以及节点的出度;
- 缺点:很难算出⼊度,需要遍历整张表;
- 因此可以同时建⽴⼀张逆连接表(相当于记录⼊度的表);
- 有向图
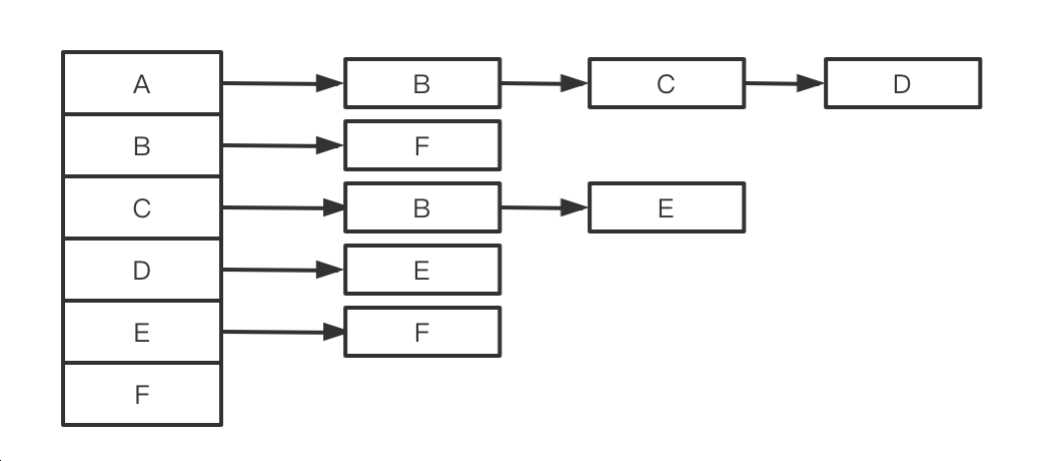
- 无向图

- 权重⽆向图
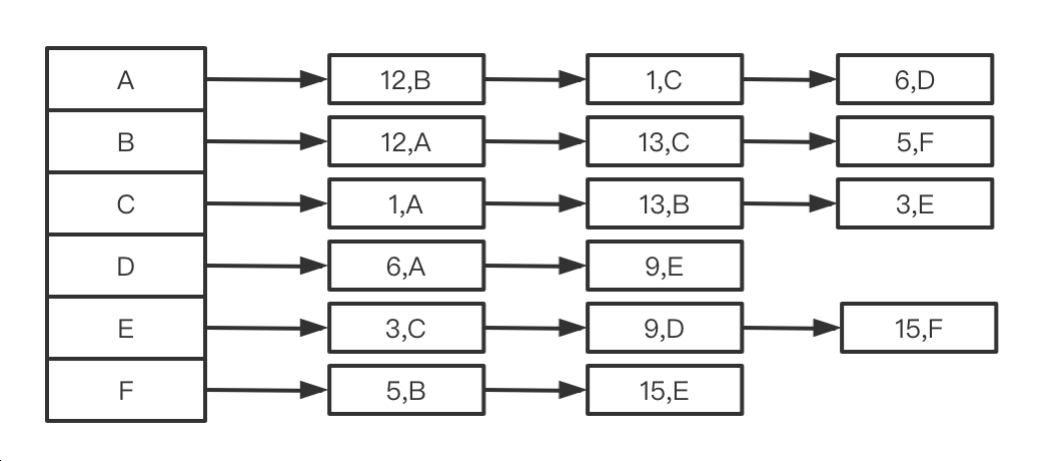
- 优点和缺点:
-
2.图的遍历方式
-
从图中某⼀个顶点出发,访问图中其余顶点,使每个顶点被访问⼀次且只被访问⼀次 -》保证不重不漏
-
可以从图中任意⼀个顶点出发进⾏遍历;
-
需要解决的问题:
- 确定⼀条搜索路径;、
- 确保每个顶点被访问到;
- 确保每个顶点只能被访问⼀次;
-
设置辅助数组visited,数组元素的初始值均为false,⼀旦遍历过就置为true;进行回溯
-
深度优先遍历dfs
- 关键数据结构:栈;
- 应用
- 检测连通分量的个数;连通分量:是两个图之间没有任何边的联系
- 两个点是否在⼀个连通分量中;
- 检测是否构成环;从⼀个点出发能否回到出发点; -》只有出度不能构成环
-
广度优先遍历bfs
- 关键数据结构:队列;
- 应用
- 游戏中找寻路径问题;
-
迪杰斯特拉算法(dijkstra) -》计算最小权重值
- 该算法主要解决最短路径问题,采⽤是贪⼼思想;
- 对象:权重图;
- 该算法核⼼思想是,
- 每次从路径最短的点出发遍历相邻边,检测修改路径值(确保相邻点也是最短),
- 从未被确认路径最短的顶点集合中选择最短路径的点,
- 将该点加⼊确认路径最短的顶点集合,并将该点作为下次遍历相邻边的出发点;
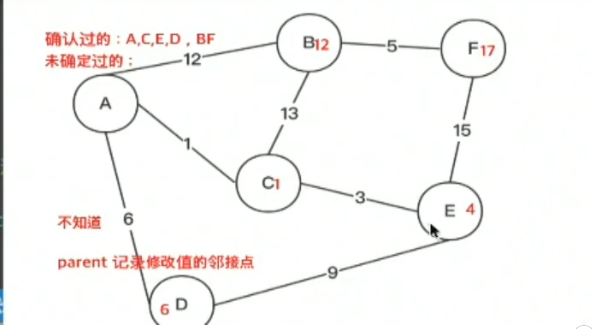
- 结束后,图中从A出发到达任何一个点的最短路径都已知了,通过parent(谁修改它路径值的父节点),即可知道最短路径
- 比如A -》E的最短路径是A -》C -》E;而E的parent为C,C的parent为A
- 核⼼步骤:更新,扫描,修改;
3.常用使用形式
-
应用场景
- ⽹络爬⾍;
- 地图应⽤:⾼德地图,百度地图(最短路径推荐,最短时⻓推荐);
- 社交⽹络分析:好友推荐,垃圾⽤户分析,社交关系分析;
- 推荐、精准营销;
- 舆情控制,信息传播;
- 防欺诈(⽹络诈骗和电信诈骗);
- 计算⽣物学:模拟分⼦运动;





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· DeepSeek在M芯片Mac上本地化部署
· 葡萄城 AI 搜索升级:DeepSeek 加持,客户体验更智能