理解递归

求一个数组的最大值

package com.sort.demo;

public class Recursion {
    public static int getMmax(int[] arr,int L,int R){
        if (L==R){
            return arr[L];
        }
        int mid=(L+R)/2;
        int lm=getMmax(arr,L,mid);
        int rm=getMmax(arr,mid+1,R);
        return Math.max(lm,rm);
    }

    public static void main(String[] args) {
        int[] arr=new int[]{1,2,9,5,7};
        int max=getMmax(arr,0,arr.length-1);
        System.out.println(max);
    }
}

思想就是把数组分成两部分，分别比较两部分的最大值，最后得出最大值；

递归就是程序帮我们压栈，jvm每个线程在执行的时候，都会产生一个栈，而栈里面都是栈帧，每个方法在执行的时候都会创建一个栈帧，栈帧里面存着：局部变量表、操作数栈、动态链接、方法的返回地址等信息

例子中的数组为：1 2 9 5 7

当main方法执行时，会创建一个栈，并压入一个栈帧，存着main方法的 局部变量表，

 

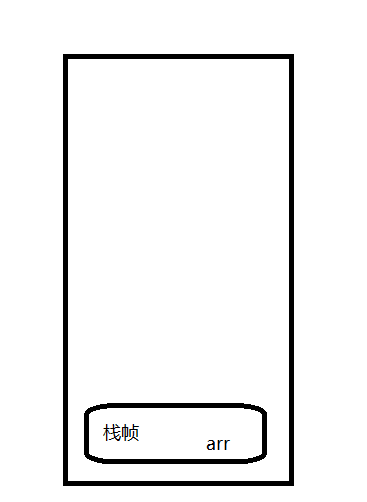
这个栈帧里面有main方法的局部变量arr，

当main方法调用getMax方法时，程序会压入另一个栈帧

 

 

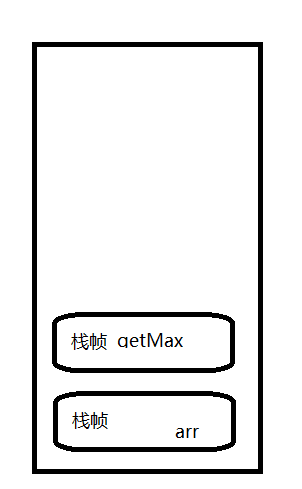
 这个栈帧会存着getMax方法的局部变量和方法返回地址

getMax方法中继续调用getMax方法，会继续将栈帧压入栈，当执行到最后一步L=R时，程序return，会从栈的最顶上弹出栈帧，还原上一步操作的现场，继续执行，

递归就是这样，利用程序压栈出栈

所以所有的递归都可以改成非递归，我们自己压栈

递归算法的时间复杂度的计算：

T(N)=aT(n/b)+O(n^d)

1）log_ba>d 时间复杂度为O(N^log_ba)

2) log_ba=d 时间复杂度为O(N^d*logN)

2) log_ba<d 时间复杂度为O(N^d)

套公式算一下求最大值的时间复杂度：

子样本量的大小为N/2，子样本有2个，最后比较最大值和返回是常数操作，时间复杂度O（1）,即a=2,b=2,d=0

所以T(N)=2T(N/2)+O(1)

然后再代入 log₂2=1>d 所以时间复杂度为O(N)

 

注:master公式仅适用于子过程规模一样的情况下