数组

数组的介绍和定义

为什么要有数组

现在需要统计某公司员工的情况，例如计算平均工资，找到最高工资等。假设该公司有80名员工，用前面所学的知识，程序首先需要声明80个变量来分别记住每位员工的工资，然后再进行操作，这样做会显得很麻烦。

为了解决这种问题，Java提供了数组供我们使用。

数组概念

数组是存储同一种数据类型多个元素的集合，也可以看成是一个容器。数组既可以存储基本数据类型，也可以存储引用数据类型。

数组的定义格式

数组类型[ ] 数组名： int[ ] array=new int[10];
数组类型数组名 [ ]：double array1[ ]=new double[10];

什么是数组的初始化

Java中的数组必须先初始化，然后才能使用。所谓初始化，就是为数组中的数组元素分配内存空间，并为每个数组元素赋值
初始化的分类：
- 动态初始化：只指定长度，由系统给出初始化值
- 静态初始化：给出初始化值，由系统决定长度
- 注意事项：这两种方式只能使用一种，不能进行动静结合
动态初始化的格式：数据类型[] 数组名=new 数据类型[数组长度]; 数组长度其实就是数组中元素的个数

//动态初始化
int[] arr=new int[10];
int arr4[]=new int[21];

//静态初始化
int[] arr2=new int[]{12,23,34,56};
//简写方式
int[] arr3={12,23,56,6};

public class ArrayDemo02 {
    public static void main(String[] args) {
        //采用动态初始化如何取出数组中的元素，以及给数组赋值
        int[] arr=new int[5];
        //数组在初始化的时候，会为每一个元素分配索引，那么这个索引从0开始
        //可以通过索引取出某个元素
        int num=arr[0];
        System.out.println(num);

        //也可以通过索引，给元素重新赋值
        int num1=arr[0]=12;
        int num2=arr[1]=13;
        int num3=arr[2]=14;
        System.out.println(num1);//12
        System.out.println(num2);//13
        System.out.println(num3);//14
    }
}

数组的常见操作

1.数组元素的遍历

//定义数组
int[] arr={12,13,14,87,32};
//遍历数组
for (int i = 0; i <arr.length ; i++) {
    System.out.println(arr[i]);
}

2.数组常见的角标越界异常

数组角标越界异常：ArrayIndexOutOfBoundsException

3.数组元素的反向遍历

//定义数组
int[] arr={12,23,34,45};
//反向遍历
for (int i = arr.length-1; i >=0 ; i--) {
    System.out.println(arr[i]);
}

4.获取数组中元素的最大值或最小值

//定义数组
int[] arr={12,23,34,45};
//获取数组中的最大值
//定义一个参照值
int max=arr[0];
for (int i = 0; i < arr.length; i++) {
    if (arr[i]>max){
        max=arr[i];
    }
}
System.out.println("数组中的最大值："+max);

//获取数组中的最小值
//定义一个参照值
int min=arr[0];
for (int i = 0; i < arr.length; i++) {
    if (arr[i]<min){
        min=arr[i];
    }
}
System.out.println("数组中的最小值："+min);

5.数组元素的反转

public class ArrayDemo05 {
    public static void main(String[] args) {
        int[] arr={34,56,97,42,12};
        //反转数组中的元素
        //思路：首尾元素互换
        for (int i = 0; i <arr.length/2 ; i++) {
            int t=arr[i];//第一个元素
            arr[i]=arr[arr.length-1-i];//最后一个元素
            arr[arr.length-1-i]=t;
        }
        //遍历数组
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i]+",");
        }
    }
}

二维数组

二维数组概述

学校的Java基础班每个班有很多学生，所以可以用数组来存储，而我们又同时有很多个Java基础班，这个也应该用一个数组来存储

如何来表示这样的数据呢？Java提供了二维数组供我们使用

由此可见：二维数组其实就是每一个元素为一维数组的数组

二维数组定义格式

数据类型[] [] 变量名=new 数据类型[m] [n];

m表示这个二维数组有多少个一维数组

n表示每一个一维数组的元素个数

public class ArrayDemo01 {
    public static void main(String[] args) {
        //二维数组其实就是元素为一维数组的数组
        //一维数组的定义方式
        //1.动态初始化一个二维数组，由我们指定数组长度，由系统为数组元素赋值默认值
        //3：我们定义了一个二维数组，长度为3
        //2：二维数组里有3个一维数组，每个一维数组的长度是2
        int[][] arr=new int[3][2];
        System.out.println(arr);
        System.out.println(arr[0]);
        System.out.println(arr[0][0]);
        //给二维数组里的每个元素重新赋值
        arr[0]=new int[2];
        arr[1]=new int[2];
        arr[2]=new int[2];
     }
  }

以下格式也可以表示二维数组：
- 数据类型数组名[] [] =new 数据类型[m] [n];
- 数据类型[] 数组名[] =new 数据类型[m] [n];
  
  这两种格式不推荐使用

public class ArrayDemo02 {
    public static void main(String[] args) {
        //二维数组定义方式2
        //静态初始化，由我们为数组赋值，由系统计算长度
        int[][] arr=new int[][]{{1,2,3},{23,34,45},{56,6,7,8}};
        //通过角标获取数组中的某个元素
        System.out.println(arr[0][2]);//3
        System.out.println(arr[1][2]);//45
        System.out.println(arr[2].length);
        //数组最后一个元素的索引=数组的长度-1
        System.out.println(arr[arr.length-1][arr[arr.length-1].length-1]);

        //二维数组静态初始化的简写方式
        int[][] arr2={{12,13},{23,45},{56,67}};

        //二维数组其他的定义方式
        int arr3[][]={{12,13},{23,45},{56,67}};
        int[] arr4[]={{12,13},{23,45},{56,67}};

        int x,y;//我定义了两个int类型的变量
        int[] g,z[];//我定义了两个数组，一个一维数组g,一个二维数组z
        g=new int[1];
        z=new int[1][2];

    }

}

二维数组的遍历

public class ArrayDemo03 {
    public static void main(String[] args) {
        int[][] arr=new int[][]{{1,2,3},{23,34,45},{56,6,7,8}};
        for (int i = 0; i < arr.length; i++) {
            for (int i1 = 0; i1 < arr[i].length; i1++) {
                System.out.println(arr[i][i1]);
            }
        }

    }
}

二维数组的练习

案例演示一：

需求：公司年销售额求和

某公司按照季度和月份统计的数据如下：单位（万元）

第一季度：22,66,44

第二季度：77,33,88

第三季度：25,45,65

第四季度：11,66,99

public class ArrayDemo04 {
    public static void main(String[] args) {
        //需求：公司年销售求和
        int[][] arr={{22,66,44},{77,33,88},{25,45,65},{21,66,99}};
        //遍历二维数组
        int sum=0;//定义一个变量用来接受最后的结果
        for (int i = 0; i < arr.length; i++) {
            for (int i1 = 0; i1 < arr[i].length; i1++) {
                sum+=arr[i][i1];
            }
        }
        System.out.println("年销售总和为："+sum);

    }
}

案例演示二：

需求：打印杨辉三角形(行数可以键盘录入)

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

import java.util.Scanner;

public class ArrayDemo05 {
    public static void main(String[] args) {
        //打印杨辉三角形
       
        /*观察发现：
        1.每一行的第一列和最后一列都是1
        2.从第三行，第二列开始，这个数字等于他上一行的前一列和上一行的本列之和
         */

        Scanner scanner=new Scanner(System.in);
        System.out.println("请输入行数");
        int n= scanner.nextInt();
        //定义二维数组，存储数据,先把行数和列数定位=为一样
        int[][] arr=new int[n][n];
        //把每一行的第一列和最后一列设置为1
        for (int i = 0; i < arr.length; i++) {
            arr[i][0]=1;
            arr[i][i]=1;
        }

        //设置中间元素
        for (int i = 0; i < arr.length; i++) {
            for (int j = 1; j <=i ; j++) {
                arr[i][j]=arr[i-1][j-1]+arr[i-1][j];
            }
        }

        //遍历二维数组
        for (int i = 0; i < arr.length; i++) {
            for (int i1 = 0; i1 <=i; i1++) {
                System.out.print(arr[i][i1]+"\t");
            }
            System.out.println();
        }
    }
}

数组的练习

需求：根据数组元素查找出该元素第一次在数组中出现的索引

方式一：遍历数组挨个去查找

public class ArrayDemo06 {
    public static void main(String[] args) {
        int[] arr={12,23,34,45,67,54,32,21};
        //根据元素查找出该元素在数组中第一次出现的索引
        int index= getIndexByEle(arr,34);
        System.out.println("该元素第一次在数组中出现的索引是："+index);
    }

    private static int getIndexByEle(int[] arr,int ele) {
        //遍历数组
        for (int i = 0; i < arr.length; i++) {
            if (ele==arr[i]){
                return i;
            }
        }

        return -1;//如果没有找到这个元素，就返回-1
    }
}

方式二：二分查找

二分查找的前提是：该数组的元素必须有序

二分查找的思想：每一次都查找中间的元素，比较大小就能减少一般的元素

查找时，我们拿着个元素和中间索引对应的元素去比较，比较之后，有三种情况：

你要找的元素正好等于中间索引所对应的元素，那么就返回中间索引，也就是说正好找到了
你要找的元素小于中间索引对应的元素，那么就改变最大索引，移动最大索引 maxIndex=centerIndex-1
你要找的元素，比中间索引对应的元素大，那么就移动最小索引 minIndex=centerIndex+1

移动之后要重新计算中间索引

public class ArrayDemo07 {
    public static void main(String[] args) {
        //二分查找，前提是数组元素必须有序
        int[] arr={11,13,24,35,57,89,90};
        int index=getIndexByEle(arr,35);
        System.out.println("该元素出现的索引是："+index);
    }

    private static int getIndexByEle(int[] arr, int ele) {
        //定义最小索引，中间索引，最大索引
        int minIndex=0;
        int maxIndex=arr.length-1;
        int centerIndex=(minIndex+maxIndex)/2;
        while(minIndex<=maxIndex){
            //如果找的这个元素等于中间索引对应的元素，就返回中间索引
            if (ele==arr[centerIndex]){
                return centerIndex;
                //如果找的元素大于中间索引对应的元素，就移动最小索引
            }else if(ele>arr[centerIndex]){
                minIndex=centerIndex+1;
                //如果找的元素小于中间索引对应的元素，就移动最大索引
            }else if(ele<arr[centerIndex]){
                maxIndex=centerIndex-1;
            }
            //重新计算中间索引
            centerIndex=(minIndex+maxIndex)/2;
        }
        return -1;//如果没有找到，就返回-1
    }
}

数组常见的排序算法

排序：把一个无序序列通过某种方式变成有序序列

冒泡排序

排序原理：数组元素两两比较，交换位置，大元素往后放，经过一轮比较后，最大的元素，就会出现在最大索引处

import java.util.Arrays;

public class ArrayDemo08 {
    public static void main(String[] args) {
        //冒泡排序
        int[] arr={12,24,69,43,27};
        //推导过程
        //第一轮比较
        for (int i = 0; i < arr.length-1; i++) {
            if (arr[i]>arr[i+1]){
                //交换位置
                int t=arr[i];
                arr[i]=arr[i+1];
                arr[i+1]=t;

            }
        }

        //第二轮比较
        for (int i = 0; i < arr.length-2; i++) {
            if (arr[i]>arr[i+1]){
                //交换位置
                int t=arr[i];
                arr[i]=arr[i+1];
                arr[i+1]=t;

            }
        }

        //第三轮比较
        for (int i = 0; i < arr.length-3; i++) {
            if (arr[i]>arr[i+1]){
                //交换位置
                int t=arr[i];
                arr[i]=arr[i+1];
                arr[i+1]=t;

            }
        }

        //第四轮比较
        for (int i = 0; i < arr.length-4; i++) {
            if (arr[i]>arr[i+1]){
                //交换位置
                int t=arr[i];
                arr[i]=arr[i+1];
                arr[i+1]=t;

            }
        }

        System.out.println(Arrays.toString(arr));
    }
}




//优化代码
public class ArrayDemo08 {
    public static void main(String[] args) {
        //冒泡排序
        int[] arr={12,24,69,43,27};
        for (int j= 0; j < arr.length-1; j++) {
            for (int i = 0; i < arr.length-1-j; i++) {
                if (arr[i]>arr[i+1]){
                    //交换位置
                    int t=arr[i];
                    arr[i]=arr[i+1];
                    arr[i+1]=t;
                }
            }
        }
        System.out.println(Arrays.toString(arr));
    }

选择排序

排序原理：从0索引处开始，依次和后面的元素进行比较，小的元素往前放，经过一轮比较后，最小的元素就出现在了最小索引处

import java.util.Arrays;

public class ArrayDemo09 {
    public static void main(String[] args) {
        //选择排序
        //推导过程
        int[] arr={24,69,43,27,12};
        //第一轮比较，从0索引开始
        int index=0;
        for (int i = 1; i < arr.length; i++) {
            if (arr[index]>arr[i]){
                int t=arr[index];
                arr[index]=arr[i];
                arr[i]=t;
            }
        }

        //第二轮比较，从1索引开始
         index=1;
        for (int i = 1+index; i < arr.length; i++) {
            if (arr[index]>arr[i]){
                int t=arr[index];
                arr[index]=arr[i];
                arr[i]=t;
            }
        }

        //第三轮比较，从2索引开始
        index=2;
        for (int i = 1+index; i < arr.length; i++) {
            if (arr[index]>arr[i]){
                int t=arr[index];
                arr[index]=arr[i];
                arr[i]=t;
            }
        }

        //第四轮比较，从3索引开始
        index=3;
        for (int i = 1+index; i < arr.length; i++) {
            if (arr[index]>arr[i]){
                int t=arr[index];
                arr[index]=arr[i];
                arr[i]=t;
            }
        }
        System.out.println(Arrays.toString(arr));
    }
}



//优化代码
public class ArrayDemo09 {
    public static void main(String[] args) {
        //选择排序
        int[] arr={24,69,43,27,12};
        for (int index = 0; index < arr.length-1; index++) {
            for (int i = 1+index; i < arr.length; i++) {
                if (arr[index]>arr[i]){
                    int t=arr[index];
                    arr[index]=arr[i];
                    arr[i]=t;
                }
            }
        }

        System.out.println(Arrays.toString(arr));
    }

插入排序

排序原理：插入排序，是一种最简单的排序方法，他的基本操作是将一个记录插入到长度为m的有序表中，使之仍保持有序

import java.util.Arrays;

public class ArrayDemo10 {
    public static void main(String[] args) {
        //插入排序
        int[] arr={23,43,56,15,76,36,21,-1,250};
        //第一种写法
        /*
        //外层循环定义轮次
        for (int i = 1; i < arr.length; i++) {
            //里层循环，进行比较插入
            int j=i;
            while(j>0&&arr[j]<arr[j-1]){
                int t=arr[j];
                arr[j]=arr[j-1];
                arr[j-1]=t;
                j--;
            }
        }*/
        //第二种写法
         for (int i = 1; i < arr.length; i++) {
            for (int j = i; j >0 ; j--) {
                if (arr[j]<arr[j-1]){
                   /* int t=arr[j];
                    arr[j]=arr[j-1];
                    arr[j-1]=t;
                    j--;*/
                   swapVaule(arr,j,j-1);
                }
            }
        }
        System.out.println(Arrays.toString(arr));
    }
    
    //单独创建一个交换方法，使用时直接调用即可
     public static void swapVaule(int[] arr,int i,int j){
        int t=arr[i];
        arr[i]=arr[j];
        arr[j]=t;
    }
}

希尔排序

希尔排序又称缩小增量排序

基本思想：先将原表按增量ht分组，每个子文件按照插入法排序。同样，用下一个增量ht/2将文件再分为子文件，再插入法排序。直到ht=1时，整个文件排好序
关键：选择合适的增量
希尔排序算法9-3：可以通过三重循环来实现

import java.util.Arrays;

public class ArrayDemo11 {
    public static void main(String[] args) {
        //希尔排序,是对插入排序的优化，核心的思想就是合理的选取增量，经过一轮排序后，就会让序列大致有序
        //插入排序其实就是增量为1的希尔排序
        int[] arr={23,43,56,15,76,36,21,250};
        shellSort(arr);
        System.out.println(Arrays.toString(arr));

    }
    private static void shellSort(int[] arr){
        //定义一个增量
        //第一轮
        int h=4;
        for (int i = h; i < arr.length; i++) {
            for (int j = i; j >h-1 ; j-=h) {
                if (arr[j]<arr[j-h]){

                    swapVaule(arr,j,j-h);
                }
            }
        }

        //第二轮
        h=2;
        for (int i = h; i < arr.length; i++) {
            for (int j = i; j >h-1 ; j-=h) {
                if (arr[j]<arr[j-h]){

                    swapVaule(arr,j,j-h);
                }
            }
        }

        //第三轮
        h=1;
        for (int i = h; i < arr.length; i++) {
            for (int j = i; j >h-1 ; j-=h) {
                if (arr[j]<arr[j-h]){

                    swapVaule(arr,j,j-h);
                }
            }
        }
        
    }
    public static void swapVaule(int[] arr,int i,int j){
        int t=arr[i];
        arr[i]=arr[j];
        arr[j]=t;
    }
}




//优化代码
public class ArrayDemo11 {
    public static void main(String[] args) {
        //希尔排序,是对插入排序的优化，核心的思想就是合理的选取增量，经过一轮排序后，就会让序列大致有序
        //插入排序其实就是增量为1的希尔排序
        int[] arr={23,43,56,15,76,36,21,250};
        shellSort(arr);
        System.out.println(Arrays.toString(arr));

    }
    private static void shellSort(int[] arr) {
          /*for (int h = 4; h > 0; h /= 2) {
             for (int i = h; i < arr.length; i++) {
                 for (int j = i; j > h - 1; j -= h) {
                     if (arr[j] < arr[j - h]) {
                         swapVaule(arr, j, j - h);
                    }
                }
            }
        }
        
    }*/
       //希尔排序的思想就是合理的选取增量
        //第一次的增量选取数组长度的一半，然后不断地减半
       /* for (int h = arr.length/2; h > 0; h /= 2) {
            for (int i = h; i < arr.length; i++) {
                for (int j = i; j > h - 1; j -= h) {
                    if (arr[j] < arr[j - h]) {
                        swapVaule(arr, j, j - h);
                    }
                }
            }
        }
    }*/
    
     //我们第一次的增量选择数组的一般，还不是很好，可以使用一种序列叫做克努特序列
       // int h=1;
        //h=h*3+1;
        //根据克努特序列，选取第一次的增量
        int jiange=1;
        while(jiange<=arr.length/3){
            jiange=jiange*3+1;

        }
        for (int h = jiange; h > 0; h=(h-1)/3) {
            for (int i = h; i < arr.length; i++) {
                for (int j = i; j > h - 1; j -= h) {
                    if (arr[j] < arr[j - h]) {
                        swapVaule(arr, j, j - h);
                    }
                }
            }
        }
    }
public static void swapVaule(int[] arr,int i,int j){
        int t=arr[i];
        arr[i]=arr[j];
        arr[j]=t;
    }
}

快速排序

算法思想：

分治法：比大小，再分区

从数组中取出一个数，作为基准数
分区：将比这个数大或等于的数全放到特他的右边，小于他的数全放到他的左边
再对左右区间重复第二步，直到各区间只有一个数

实现思路：

挖坑填数：

将基准数挖出形成第一个坑
由后向前找比他小的数，找到后挖出此数填到前一个坑中
由前向后找比他大或等于的数，找到后也挖出此数填到前一个坑中
再重复执行2，3步骤

public class QuickSortUtils {
    //快速排序
    public static void quickSort(int[] arr,int start,int end){
        //找出分左右两区的索引位置，然后对左右两区进行递归调用
        if (start<end){
            int index=getIndex(arr,start,end);
            quickSort(arr,start,index-1);
            quickSort(arr,index+1,end);
        }
    }

    private static int getIndex(int[] arr, int start, int end) {
        int i=start;
        int j=end;
        int x=arr[i];
        while(i<j){
            //由后向前找比他小的数，找到后挖出此数填到前一个坑中
            while(i<j&&arr[j]>=x){
                j--;
            }
            if (i<j){
                arr[i]=arr[j];
                i++;
            }
            //由前向后找比他大或等于的数，找到后也挖出此数填到前一个坑中
            while(i<j&&arr[i]<x){
                i++;
            }
            if (i<j){
                arr[j]=arr[i];
                j--;
            }

        }
        arr[i]=x;//把基准数填到最后一个坑里
        return j;
    }
}




import java.util.Arrays;

public class ArrayDemo12 {
    public static void main(String[] args) {
        //定义一个数组
        int[] arr={10,3,5,6,1,0,100,40,50,8};
        //调用工具类，进行快速排序，传入数组，传入起始位置，传入结束位置
        QuickSortUtils.quickSort(arr,0,arr.length-1);
        //输出排序后的结果
        System.out.println(Arrays.toString(arr));
    }
}

归并排序

算法思想：归并排序就是利用归并的思想实现排序的方法。它的原理是假设初始序列有N个记录，则可以看成是N个有序的子序列，每个子序列的长度为1，然后两两归并，得到N/2个长度为2或1的有序子序列，再两两归并，如此重复，直至得到一个长度为N的有序序列为止，这种排序方法称为2路归并排序。

import java.util.Arrays;

public class ArrayDemo13 {
    public static void main(String[] args) {
        //归并排序
        //原始待排序数组
        int[] arr={10,30,2,1,0,8,7,5,19,29};
        //我们先给左右两边是有序的一个数组，先来进行归并排序
        //int[] arr ={4,5,7,8,1,2,3,6} ;
        //拆分
        chaiFen(arr,0,arr.length-1);
        //归并
        // guiBing(arr,0,3,arr.length-1);

        //输出原数组
        System.out.println(Arrays.toString(arr));

    }

    private static void chaiFen(int[] arr, int startIndex, int endIndex) {
        //计算中间索引
        int centerIndex=(startIndex+endIndex)/2;
        if(startIndex<endIndex){
            chaiFen(arr,startIndex,centerIndex);
            chaiFen(arr,centerIndex+1,endIndex);
            guiBing(arr,startIndex,centerIndex,endIndex);
        }
    }


    private static void guiBing(int[] arr, int startIndex, int centerIndex, int endIndex) {
        //定义一个临时数组
        int[] arr1=new int[endIndex-startIndex+1];
        //定义左边数组的起始索引
        int i=startIndex;
        //定义右边数组的起始索引
        int j=centerIndex+1;
        //定义临时数组的起始索引
        int index=0;
        //比较左右两个数组的元素大小，往临时数组中放
        while (i<=centerIndex&&j<=endIndex){
            if (arr[i]<=arr[j]){
                arr1[index]=arr[i];
                i++;
            }else{
                arr1[index]=arr[j];
                j++;
            }
            index++;
        }
        //处理剩余元素
        while (i<=centerIndex){
            arr1[index]=arr[i];
            i++;
            index++;
        }
        while (j<=endIndex){
            arr1[index]=arr[j];
            j++;
            index++;
        }
        //System.out.println(Arrays.toString(arr1));
        //将临时数组中的元素取到原数组中
        for (int k = 0; k <arr1.length ; k++) {
            arr[k+startIndex]=arr1[k];
        }
    }

}

基数排序

基数排序不同于之前所介绍的各类排序

前边介绍的排序方法或多或少的是通过使用比较和移动记录来实现排序，而基数排序的实现不需要进行关键字的比较。只需要对关键字进行“分配”与“收集”两种操作即可

import java.util.Arrays;

public class ArrayDemo14 {
    public static void main(String[] args) {
        //基数排序
        int[] arr={2,1,5,21,31,234,444,56,47,10,903,100,435,4628,465,294,672};
        //确定排序轮次
        //获取数组中的最大值
        // int max=getMax(arr);
        //基数排序
        sortArray(arr);

        //输出排序过后的数组
        System.out.println(Arrays.toString(arr));
    }

    private static void sortArray(int[] arr) {
        //定义二维数组，放是个桶
        int[][] tempArr=new int[10][arr.length];
        //定义统计数组
        int[] count=new int[10];
        int max=getMax(arr);
        int len=String.valueOf(max).length();
        //循环轮次
        for (int i = 0,n=1; i < len; i++,n*=10) {
            for (int i1 = 0; i1 < arr.length; i1++) {
                //获取每个位置上的数字
                int ys=arr[i1]/n%10;
                tempArr[ys][count[ys]++]=arr[i1];
            }
            //取出桶中的元素
            int index=0;
            for (int k = 0; k < count.length; k++) {
                if (count[k]!=0){
                    for (int h = 0; h < count[k]; h++) {
                        //从桶中取出元素，放回原数组
                        arr[index]=tempArr[k][h];
                        index++;
                    }
                    count[k]=0;//清除上一次统计的个数
                }
            }
        }
    }

    private static int getMax(int[] arr) {
        int max=arr[0];
        for (int i = 1; i <arr.length ; i++) {
            if (arr[i]>max){
                max=arr[i];
            }
        }
        return max;
    }
}

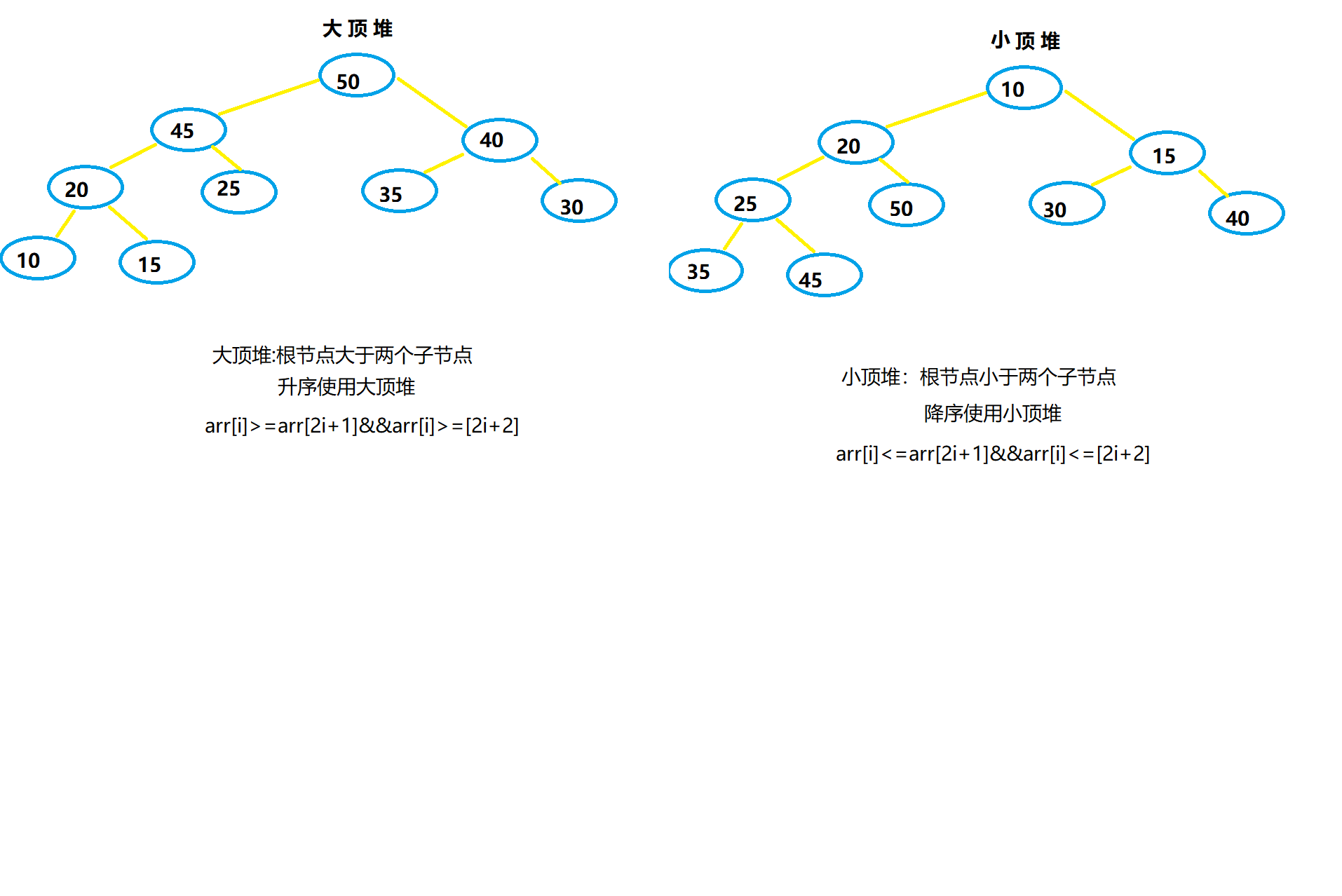
堆排序

堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序

基本思想：

将待排序的序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点
将其与末尾元素进行交换，此时末尾就为最大值
然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值
如此反复执行，便能得到一个有序序列

import java.util.Arrays;

public class ArrayDemo15 {
    public static void main(String[] args) {
        //堆排序
        int[] arr={1,0,6,7,2,3,4,10,5,9,32};
        //调整大顶堆的方法
        //定义开始调整的位置
        int startIndex=(arr.length-1)/2;
        //循环开始调
        for (int i=startIndex;i>=0;i--){
            toMaxHeap(arr,arr.length,i);
        }

        //经过上边的操作后，已经把数组变成了大顶堆，把根元素和最后一个元素进行交换
        for (int i = arr.length-1; i >0 ; i--) {
            //进行调换
            int t=arr[0];
            arr[0]=arr[i];
            arr[i]=t;
            //换完之后，再把剩余元素调成大顶堆
            toMaxHeap(arr,i,0);
        }
        System.out.println(Arrays.toString(arr));
    }

    /**
     *
     * @param arr 要排序的数组
     * @param size 要调整的元素个数
     * @param index 从哪里kaishitiaoz
     */

    private static void toMaxHeap(int[] arr, int size, int index) {
        //获取左右子节点的索引
        int leftNodeIndex=index*2+1;
        int rightNodeIndex=index*2+2;
        //查找最大节点对应的索引
        int maxIndex=index;
        if (leftNodeIndex<size&&arr[leftNodeIndex]>arr[maxIndex]){
            maxIndex=leftNodeIndex;
        }
        if (rightNodeIndex<size&&arr[rightNodeIndex]>arr[maxIndex]){
            maxIndex=rightNodeIndex;
        }
        //调换位置
        if (maxIndex!=index){
            int t=arr[maxIndex];
            arr[maxIndex]=arr[index];
            arr[index]=t;
            //调换之后，可能会影响到下边的子树，不是大顶堆，还需要再次调换
            toMaxHeap(arr,size,maxIndex);
        }
    }
}

发表于 2021-08-09 15:39 渐变拿铁的黑咖啡阅读(30) 评论(0) 编辑收藏举报

刷新页面返回顶部

数组

数组