SVD专题2 线性映射的奇异值分解——矩阵形式的推导

目录

image

2021-11-9 分割线

麻烦各位看官大大们多多点赞哦，让更多的人看到这篇文章~

以下是原文：

SVD专题2 线性映射的奇异值分解——矩阵形式的推导

前言 Preface

本讲不能和本系列的第1讲：SVD专题1 算子的奇异值分解——矩阵形式的推导 - 夏小正的鲜小海 - 博客园 采取同样的讲解策略，原因是线性映射不同于算子，涉及到维度的变化，倘若对线性代数的几个基本定理没有理解的话，很难看懂每一步都是想做什么。

几点说明：

第一点，为什么在第1讲的推导中用的是符号 \(T\) ，这里是符号 \(A\) 呢？

一方面是我在写这部分内容时参考的两大资料来源：線代啟示錄 和 一份 CMU 的课程讲义 Computer Science Theory for the Information Age, Spring 2012. 都是用的 \(A\) ，另一方面是，符号 \(T\) 其实是沿袭了 "Linear Algebra Done Right" 中将其视作算子或线性映射的习惯表达，而 SVD 在具体应用中基本都是在和矩阵打交道的，而用 \(T\) 来表达矩阵的很少。这里为了与人们的习惯用法保持一致，故使用记号 \(A\) 。

第二点，下面的出现的向量空间默认是复向量空间或复内积向量空间。

特别注意，本节中出现的 \(A\) 有两重含义：当把 \(A\) 看作代数语言，它表示一个抽象的线性映射；当使用矩阵语言，把 \(A\) 视作该线性映射对应的矩阵表述，那么 \(A\) 就是 \(\mathbb{C}^{M\times N}\) 中的一个实实在在的矩阵。

预备知识 Prerequisite

2.1 秩-零定理 Rank-Nullity Theorem

作为后面推导的基石，一定要搞懂这个线性代数中最基本的一大定理。

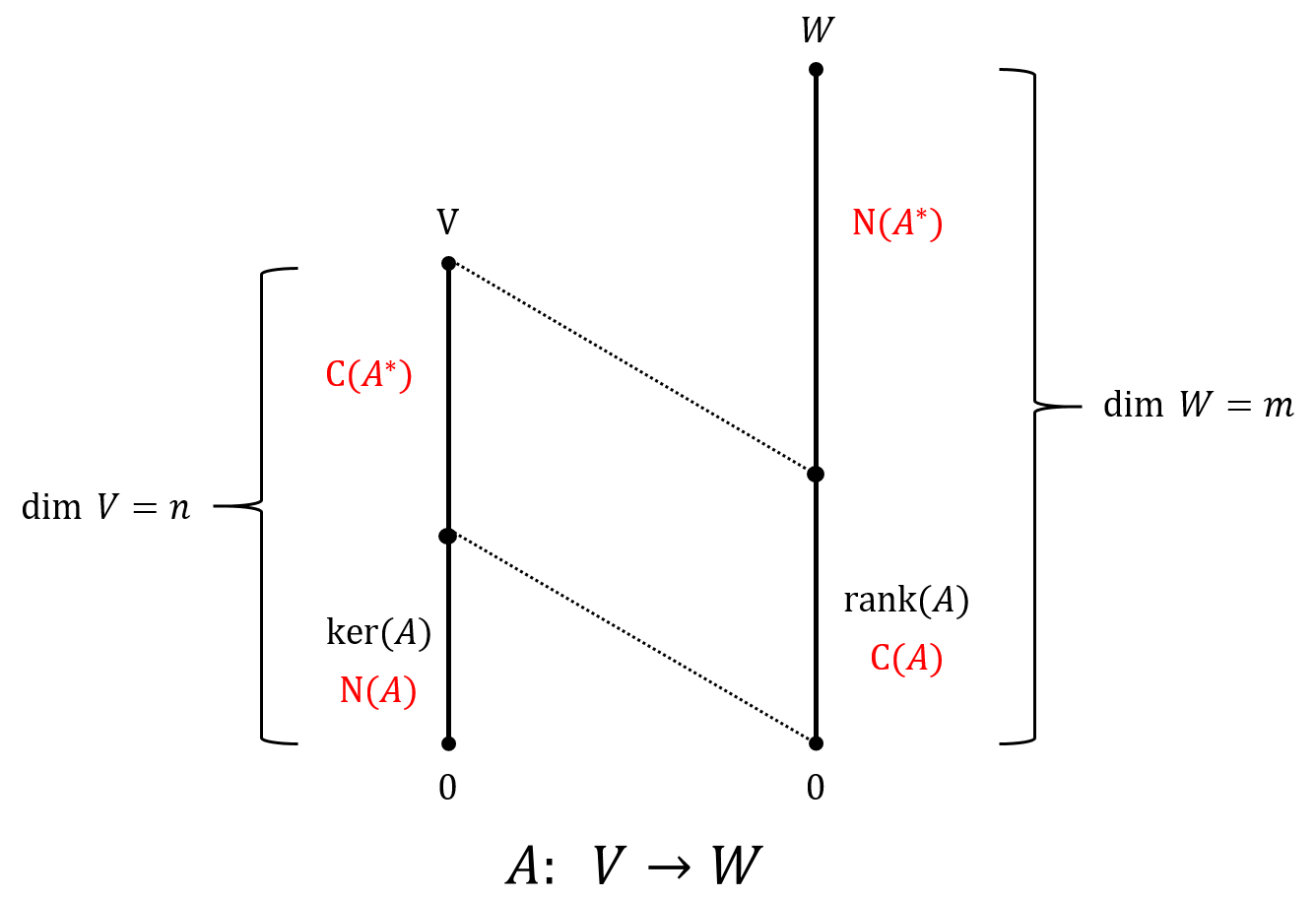
考虑由 \(n\) 维复向量空间 \(V\) 到 \(m\) 维复向量空间 \(M\) 的一个线性映射 \(A:V \mapsto W\)。我们把 \(V\) 中那些被 \(A\) 映射到 \(W\) 中 \(\mathbf{0}\) 向量的全体向量，叫做 \(A\) 的零空间 \(\operatorname{null}{A}\) （或称核空间 \(\operatorname{ker}{A}\) ），把 \(V\) 中所有向量都映射到 \(W\) 中去，相应的被映射的值域，叫做 \(A\) 的值空间 \(\operatorname{range}{A}\) 。不难证明， \(\operatorname{ker}{A}\) 是 \(V\) 的一个子空间， \(\operatorname{range}{A}\) 是 \(W\) 的一个子空间，并且称值空间 \(\operatorname{range}{A}\) 的维度为线性映射 \(A\) 的秩，记作 \(\operatorname{rank}{A}\) （不要忘了，子空间的维度 = 基中线性独立的向量的个数）。

秩零定理告诉我们， \(V\) 的维度，一定等于 \(\operatorname{ker}{A}\) 的维度与 \(\operatorname{range}{A}\) 的维度之和，即：

\[n = \operatorname{dim}{V} = \operatorname{dim}{\operatorname{ker}{A}} + \operatorname{dim}{\operatorname{range}{A}}\\ \]

这个定理的证明是很重要的，蕴含了一个很有用的想法，这个想法将作为后续 SVD 推导的出发点，有助于直观理解。现在给出该定理在代数视角下的证明。

如果设 \(\operatorname{ker}{A}\) 的维度是 \(p\) ，一组基为 \(\{\mathbf{u_1}, ..., \mathbf{u_p}\}\) ，那么我们可以在这组基的基础上将其扩充成 \(V\) 的一组基 \(\{\mathbf{u_1}, ..., \mathbf{u_p}, \mathbf{v_1}, ..., \mathbf{v_r}\}\) ，即我们又新增了 \(r\) 个线性独立的向量。那么 \(V\) 的维度 \(n=p+r\) 。其实不难看出，这里其实相当于构造出来了一个子空间 \(\operatorname{span}\{\mathbf{v_1}, ..., \mathbf{v_r}\}\) ，这个子空间把 \(\{\mathbf{v_1}, ..., \mathbf{v_r}\}\) 作为它的基。现在 \(V\) 中就有两个子空间了，分别是 \(\operatorname{ker}{A}\) 和 \(\operatorname{span}\{\mathbf{v_1}, ..., \mathbf{v_r}\}\) 。它们刚好凑成了二元直和分解， \(\operatorname{ker}{A} \oplus \operatorname{span}\{\mathbf{v_1}, ..., \mathbf{v_r}\}=V\) 。直和在这里可以简单的理解为“互不隶属”。

既然有了一组基 \(\{\mathbf{u_1}, ..., \mathbf{u_p}, \mathbf{v_1}, ..., \mathbf{v_r}\}\) ，很自然的想法是 \(V\) 中的每一个向量 \(\mathbf{v}\) 都可以写为基的线性组合：

\[\begin{aligned} A\mathbf{v}&=a_1\mathbf{u_1}+\cdots+a_p\mathbf{u_p}+ b_1\mathbf{v_1}+\cdots+b_r\mathbf{v_r} \\ &=b_1A\mathbf{v_1}+\cdots+b_rA\mathbf{v_r} \end{aligned}\\ \]

第二个等号成立的原因是 \(A\) 把 \(\mathbf{u_1}\) 到 \(\mathbf{u_p}\) 都给映射为 \(W\) 中的 \(\mathbf{0}\) 向量了，或者说每个 \(\mathbf{u_i}\) 都在 \(\operatorname{ker}{A}\) 中。

上式说明 \(\operatorname{range}{A}\) 其实就是 \(\operatorname{span}\{b_1A\mathbf{v_1}+\cdots+b_rA\mathbf{v_r}\}\)。如果能够证明 \(\{A\mathbf{v_1}, ..., A\mathbf{v_r}\}\) 是线性独立集，那么 \(\operatorname{range}{A}\) 的维度恰好就为 \(r\) ，定理就得证了。下面证明 \(\{A\mathbf{v_1}, ..., A\mathbf{v_r}\}\) 的确是线性独立集，即 \(\{A\mathbf{v_1}, ..., A\mathbf{v_r}\}\) 是 \(\operatorname{range}{A}\) 的一组基。

令： \(c_1 A\mathbf{v_1}+\cdots+ c_r A\mathbf{v_r}=0\) ，有：

\[\begin{aligned} & c_1 A\mathbf{v_1}+\cdots+ c_r A\mathbf{v_r}= \mathbf{0} \\ \Longleftrightarrow \ & A \left( c_1 \mathbf{v_1}+\cdots+ c_r \mathbf{v_r} \right)= \mathbf{0} \end{aligned}\\ \]

意味着 \(c_1 \mathbf{v_1}+\cdots+ c_r \mathbf{v_r}\) 在 \(\operatorname{ker}{A}\) 中，必然可以用 \(\operatorname{ker}{A}\) 的基 \(\{\mathbf{u_1}, ..., \mathbf{u_p}\}\) 来表示，不妨表示为：

\[c_1 \mathbf{v_1}+\cdots+ c_r \mathbf{v_r} = d_1 \mathbf{u_1}+\cdots+ d_p \mathbf{u_p}\\ \]

注意到 \(\{\mathbf{u_1}, ..., \mathbf{u_p}, \mathbf{v_1}, ..., \mathbf{v_r}\}\) 正是 \(V\) 的基，故所有系数都必须为 \(0\) 才能使上式成立，即唯有 \(c_1=\cdots=c_r=0\) 才能使 \(c_1 A\mathbf{v_1}+\cdots+ c_r A\mathbf{v_r}=0\) 。说明 \(\{A\mathbf{v_1}, ..., A\mathbf{v_r}\}\) 的确是线性独立集，恰好可以作为 \(\operatorname{range}{A}\) 的一组基，那么 \(\operatorname{range}{A}\) 的维度就是基中向量的个数为 \(r\) ，秩零定理得证。 \(\blacksquare\)

事实上，上面的论述都是从代数的角度来讲的，但其实线性映射 \(A\) 是和矩阵 \(A\) 存在一一对应关系的，我们把这种对应关系称之为同构。那么在矩阵语言下，秩零定理怎样表示呢？

首先引入概念：矩阵 \(A\) 的列空间 \(C(A)\) 和零空间 \(N(A)\) 。对应关系为： \(C(A)\) 对应线性映射 \(A\) 的值空间 \(\operatorname{range}{A}\) ， \(N(A)\) 对应线性映射A的核空间 \(\operatorname{ker}{A}\) 。

\[\begin{aligned} C(A)&=\left\{A \mathbf{x} \mid \mathbf{x} \in \mathbb{C}^{n}\right\} \\ N(A)&=\left\{\mathbf{x} \in \mathbb{C}^{n} \mid A \mathbf{x}=0\right\} \end{aligned}\\ \]

那么秩零定理用矩阵语言的等价表述就是：

\[n = \operatorname{dim}{\mathbb{C}^{n}} = \operatorname{dim}{N(A)} + \operatorname{dim}{C(A)}\\ \]

线性变换用语和矩阵用语的详细说明可见線性變換與矩陣的用語比較。

题外话：在上述的证明过程中，隐约感觉到将 \(V\) 拆分为 \(\operatorname{ker}{A}\) 和另一子空间的直和的这个思路有点儿意思，但好像又没得到很好玩的性质和结论。这其实是没有在向量空间中引入“度量”，具体点来说就是没有引入内积运算，倘如引入内积，会有很好玩的结论在前面等着我们，下小节我们再来说。

2.2 最核心的四个子空间

本节前言（可忽略不看，不影响主线论述）

四个基本子空间的引入其实有两种方法，从矩阵角度引入相对简单，比如先从实矩阵引入，这也是线代启示录中的做法，直接抛开内积的引入，讨论 \(C(A)\) ， \(C(A^T)\) ， \(N(A)\) ， \(N(A^T)\) 的关系。然而从我的角度来看，由于矩阵和矩阵的转置实在太过形象了，从实矩阵的角度深入往里走，总有种管中窥豹的感觉，始终看不到映射的“全貌”。初学者产生类似于“行秩和列秩为何如此巧合的相等”等问题，无法得到很好的解决，当然不是说这真的是个“巧合”，而是从实矩阵出发，真的很难看到“实质”，周老师作者本人也对这个问题作出了回答，参见答Avis──關於行秩等於列秩的幾何背景。

原回答的部分内容如下：

網友Avis留言：

老师你好，经常关注你的Blog“线性代数启示录”，很喜欢里面的内容。这里有一个问题想请教一下，是学习线性代数多年来觉得比较有意思的地方，为什么矩阵的行秩等于列秩？当然我这里问的不是怎么证明，而是想问是否有更为本质的几何和物理背景？对于几何背景不限于行空间的维数等于列空间维数这样的，而是更想知道到底是怎么样一种结构，使得行列空间秩相同。我之前一直把这个结论，认为是数学的一种“巧合”。在这样的“巧合”之下我们对于一个矩阵就只用定义一个秩 (因为行列秩相同)。

周老师的部分回答：

矩阵A的列秩等于行秩， \(\operatorname{rank}{A} = \operatorname{rank}{A^{T}}\) ，只是一个表象，隐藏其下的深层含义是矩阵 \(A\) 的列秩等于其共轭转置 \(A^*\) 的列秩。

鉴于此，不如直接对最最一般的情况进行分析，这样看的可能会更清晰些，毕竟复数域是实数域的扩充，复向量空间“可能”会有更好的性质。

2.2.1 由秩零定理引发的思考和疑问

首先把（2.1）的末尾再次强调如下：

我们在秩零定理的证明中人为构造了一个 \(\operatorname{span}\{\mathbf{v_1}, ..., \mathbf{v_r}\}\) 并且有

\[\operatorname{span}\{\mathbf{v_1}, ..., \mathbf{v_r}\} \cong \operatorname{span}\{A\mathbf{v_1}, ..., A\mathbf{v_r}\} =\operatorname{range}{A} \cong C\left(A\right)\\ \]

虽然有 \(\operatorname{span}\{\mathbf{v_1}, ..., \mathbf{v_r}\}\) ，但不禁疑问，这样由随机选取的基构成的子空间 \(\operatorname{span}\{\mathbf{v_1}, ..., \mathbf{v_r}\}\) ，性质真的好吗？

如果我们通过在向量空间引入一种“度量机制”，即定义内积，引入一个与 \(\operatorname{ker}{A}\) “正交”的子空间，就好像一个二维平面和它的法向量那样的正交关系一样，会不会有什么更好的结论？

答案是肯定的。但首先我们要引入向量空间的内积。

2.2.2 标准内积与共轭映射 Adjoint

定义向量空间 \(V\) 上的标准内积：

\[\langle{ \mathbf{x} \,, \mathbf{y} }\rangle=\mathbf{x}^* \mathbf{y}\\ \]

备注：事实上，这里我偷懒了，向量空间上的标准内积是由几条运算性质共同定义的，这里我简单这样表示，为了与后面的实际坐标系统中的内积运算保持写法上的一致。

如果取 \(F=\mathbb{C}\) ，那么 \(\mathbb{C}^{n}\) 上的内积可以写为：

\[\begin{aligned} \langle{ \mathbf{x} \,, \mathbf{y} }\rangle =\mathbf{x}^* \mathbf{y} = \left[\begin{array}{lll}x_{1}^* & \ldots & x_{n}^*\end{array}\right] \left[\begin{array}{c}y_1 \\ \vdots \\ y_{n}\end{array}\right]\\ \end{aligned}\\ \]

现在引入一个新的映射，称为 \(A\) 的共轭映射，记作 \(A^*\)（或者\(A^H\)，\(A^\dagger\)）。定义为 \(A^*: W \mapsto V\)，满足对所有的 \(\mathbf{w} \in W\) 和 \(\mathbf{v} \in V\)，都有：

\[\langle{ \mathbf{w} \,, A\mathbf{v} }\rangle=\langle{ \mathbf{v} \,, A^*\mathbf{w} }\rangle\\ \]

做一点小小的说明，这其实是借助了里斯表示定理来定义的（见 "Linear Algebra Done Right 3rd Edition" 的相应两部分：(6.42)和(7.2)）。对本文的主线而言，无需深究，不妨直接承认这种由内积定义引出的共轭映射 \(A^*\) 的合理性。

可以证明的是，上面定义的这个 \(A^*\) 一定是一个线性映射，并且还具有极其优越的性质：

\[\begin{aligned} \operatorname{range}{A^*} &\perp \operatorname{ker}{A} \quad \quad \operatorname{range}{A^*} \oplus \operatorname{ker}{A}=V \\ \operatorname{range}{A} &\perp \operatorname{ker}{A^*} \quad \quad \operatorname{range}{A} \oplus \operatorname{ker}{A^*}=W\\ \end{aligned}\\ \]

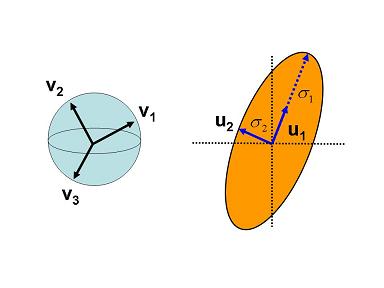
下图将有助于直观理解和记忆这个性质：

image

备注：这个帮助理解和记忆的示意图是我参照 WiKi 的 SVD 词条的配图修改而来的，加入了一些我个人的理解，该图片最初是以实矩阵语言为例画的，需要把共轭转置换成转置，当时画的时候还没有考虑复空间。

2.2.3 映射最清晰的表示？

其实到这里，可以看出些端倪了：与（2.1.1）证明过程中出现的 \(\operatorname{span}\{\mathbf{v_1}, ..., \mathbf{v_r}\}\) 相对应的概念，在这里变为了 \(\operatorname{range}{A}\) 。

（2.1.1）的证明过程中出现的同构关系（还记得当时我们还没有引入内积运算）： \(\operatorname{span}\{\mathbf{v_1}, ..., \mathbf{v_r}\} \cong \operatorname{range}{A}\)

类比到这里，也是有类似的同构关系： \(\operatorname{range}{A}^* \cong \operatorname{range}{A}\)

虽然有了同构关系： \(\operatorname{range}{A}^* \cong \operatorname{range}{A}\) ，但问题的关键在于，怎么确定（找到）一个好的“同构映射”，使得一一对应关系有最最清晰的表达？换句话来说，怎么确定 \(V\) 中的一组基和 \(W\) 中的一组基，使得同构关系通过基之间的映射越简单越好，甚至贪婪到：能从各自的基中，挑出“最好”的 \(r\) 个线性独立向量来，满足：

\[A\mathbf{v_i}=\sigma_i \mathbf{u_i} \quad i=1,...,r\\ \]

至于怎么看出满足这个条件是“最好”的，颇费一番思索，它源于对另一个“巧合”的仔细观察。

这个“巧合”是什么先直接摆在这里：正算子 \(A^*A\) 和 \(AA^*\) 有数量相同且相等的非零特征值。

接下来介绍这个有趣的结论，并且写出它的证明过程，看能观察出什么名堂出来：

2.3 \(A^*A\) 和 \(AA^*\) 有数量相同且相等的非零特征值

不难看出， \(A^*A\) 是 \(V\) 上的算子， \(AA^*\) 是 \(W\) 上的算子。

首先证明 \(A^*A\) 是正算子，即对任意的 \(\mathbf{v}\in V\) 都有：

\[\langle{ A^*A\mathbf{v} \,, \mathbf{v} }\rangle \geq 0 \\ \]

Proof：这里补充一下标准内积定义中的一条性质：

\[\langle{ \mathbf{x} \,, \mathbf{y} }\rangle = \overline{ \langle{ \mathbf{y} \,, \mathbf{x} }\rangle } \\ \]

回想一下 \(A^*\) 的定义：

\[\langle{ \mathbf{w} \,, A\mathbf{v} }\rangle=\langle{ \mathbf{v} \,, A^*\mathbf{w} }\rangle \\ \]

结合上面两点，有：

\[\langle{ A^*A\mathbf{v} \,, \mathbf{v} }\rangle = \overline{ \langle{ \mathbf{v} \,, A^*A\mathbf{v} }\rangle } = \overline{ \langle{ A\mathbf{v} \,, A\mathbf{v} }\rangle } \geq 0 \\ \]

同样的，可以得到 \(AA^*\) 是 \(W\) 上的正算子。 \(\blacksquare\)

其实 \(A^*A\) 和 \(AA^*\) 的矩阵形式有一个特殊的名字，叫做 Gramian 矩阵，详见特殊矩陣 (14)：Gramian 矩陣。

还记得我在算子的奇异值分解一文中说过的：看到能谱分解的算子一定要先分解看看，看能得到什么，要有条件反射般的直觉，并且直觉告诉我们，结论肯定是用的。

在这里，我再重新整理一遍，后面会继续用到它的，重要的概念值得重复。

2.3.1 回顾算子谱定理

算子按所具备性质的强弱程度，可以得到如下关系：

\[\operatorname{positive} \Rightarrow \operatorname{self adjoint} \Rightarrow \operatorname{normal}\\ \]

正算子的要求最苛刻，故正算子一定都是自伴算子（ Hermitian 算子）。而自伴算子又一定是正规算子。当然，第一个箭头的反向有时也可以成立。即：自伴算子 \(A\) 若满足条件 \(b^2<4c\) 且 \(b,c \in R\) ，则 \(A^2+bA+cI\) 肯定是一个正算子。（ 详见 "Linear Algebra Done Right 3rd Edition" 的 7.32(b) ）

复谱定理说， \(F=\mathbb{C}\) 上， \(A\) 是正规算子就可以谱分解，即正规算子 \(A\) 可以被其单位特征向量所确立的等距同构给对角化表示。此时条件是比较弱的，体现在： \(A\) 的特征值不一定都是实数。

实谱定理说， \(F=\mathbb{R}\) 上， \(A\) 至少是自伴算子才可以谱分解，即自伴算子 \(A\) 可以被其单位特征向量所确立的等距同构给对角化表示。此时条件（性质）强了很多，体现在： \(A\) 的特征值一定都是实数，但不一定都是非负的。

相应的， \(A\) 若是正算子，肯定也能谱分解，而且性质最好，体现在：此时 \(A\) 的特征值一定是非负的。（矩阵语言就是说矩阵 \(A\) 是半正定的）

复习到这里，对后面推导最重要的一点已经浮出水面了：正算子的一大好处是它具有完整的一组特征向量，可以张成整个向量空间，并且每个特征向量对应的特征值都是非负实数。

2.3.2 对 \(A^*A\) 谱分解

既然 \(A^*A\) 和 \(AA^*\) 分别都是正算子，不妨先来谱分解一下，说不定能得到什么有益的启发：

设 \(A\) 的秩为 \(r\) ，即：

\[\dim \operatorname{range}{A} = \operatorname{rank}{A} = r\\ \]

可以证明， \(V\) 上的算子 \(A^*A\) 和 \(W\) 上的算子 \(AA^*\) 并不会改变 \(V\) 到 \(W\) 上线性映射 \(A\) 的值空间的维度（利用 Gramian 矩陣證明行秩等於列秩，文中提到了 \(\operatorname{null}{A}\) 其实和 \(\operatorname{null}{A^*A}\) 是同一个子空间），即：

\[\operatorname{rank}{A^*A} = \operatorname{rank}{AA^*} = \operatorname{rank}{A} = r\\ \]

\(A^*A\) 可以在 \(n\) 个单位正交的特征向量 \(\mathbf{v}_{1}, \ldots, \mathbf{v}_{n}\) 上进行分解，但是其中只有 \(r\) 个对应的特征值为正实数，其余的 \(n-r\) 个特征值都为 0 。这意味着，对 \(A^*A\) 进行谱分解，令 \(\sigma_{i}=\sqrt{\lambda_{i}}\) 并且对所有 \(n\) 个特征值从大到小排个序 \(\lambda_{1} \geq \cdots \geq \lambda_{r}>0, \quad \lambda_{r+1}=\cdots=\lambda_{n}=0\) 则有：

\[\begin{aligned} A^{*} A \mathbf{v}_{i}&=\sigma_{i}^2 \mathbf{v}_{i}, \quad \ 1 \leq i \leq r \\ A^{*} A \mathbf{v}_{i}&=\mathbf{0} , \quad r+1 \leq i \leq n \end{aligned}\\ \]

此时我们有一个惊人的发现， \(W\) 上的算子 \(AA^*\) 居然也恰好有 \(r\) 个与前面 \(V\) 上算子 \(A^*A\) 相等的非零特征值！

2.3.3 \(AA^*\) 同 \(A^*A\) 的非零特征值相同

这个惊人可以严谨的表述为：若 \(\operatorname{rank}{A^*A} = \operatorname{rank}{AA^*} = \operatorname{rank}{A} = r\) ，并且特征值有序排列，则有：

\[\begin{aligned} \lambda_i\left( AA^* \right) &= \lambda_i\left( A^*A \right) = \sigma_{i}^2, \ \ \ \ \ \quad 1 \leq i \leq r \\ \lambda_i\left( AA^* \right) &= \lambda_i\left( A^*A \right) = 0, \quad r+1 \leq i \leq n \end{aligned}\\ \]

证明相当弱智：

考虑 \(AA^*\) 同时作用于 \(A\mathbf{v_i}=\mathbf{u_i}\) 的两边，其中 \(\mathbf{v_i}\) 取自前面提到的 \(A^*A\) 的 \(n\) 个单位正交的特征向量 \(\mathbf{v}_{1}, \ldots, \mathbf{v}_{n}\) 中，则：

\[AA^*\mathbf{u_i} = \left(AA^*\right) A\mathbf{v_i} = A \left(A^*A \mathbf{v_i}\right) = A \left( \lambda_i\mathbf{v_i} \right) = \lambda_i A \mathbf{v_i} = \lambda_i \mathbf{u_i}\\ \]

直接观察最左边和最右边，多巧啊，遍历所有的 \(1 \leq i \leq r\) ，说明 \(AA^*\) 的 \(r\) 个非零特征值确实和 \(A^*A\) 的 \(r\) 个非零特征值都相等。 \(\blacksquare\)

还记得我们的目标是什么吗？我再重复一下好了，不然真的很容易忘了讨论这么一大堆到底在干嘛了：

虽然有了同构关系： \(\operatorname{range}{A}^* \cong \operatorname{range}{A}\) ，但问题的关键在于，怎么确定（找到）一个好的“同构映射”，使得一一对应关系有最最清晰的表达？换句话来说，怎么确定 \(V\) 中的一组基和 \(W\) 中的一组基，使得同构关系通过基之间的映射越简单越好，甚至贪婪到：能从各自的基中，挑出“最好”的 \(r\) 个线性独立向量来，满足：

\[A\mathbf{v_i}=\sigma_i \mathbf{u_i} \quad i=1,...,r \]

至于怎么看出满足这个条件是“最好”的，颇费一番思索，它源于对另一个“巧合”的仔细观察。

这个“巧合”是什么先直接摆在这里：正算子 \(A^*A\) 和 \(AA^*\) 有数量相同且相等的非零特征值。

接下来介绍这个有趣的结论，并且写出它的证明过程，看能观察出什么名堂出来：

注意到：一串连等中间出现了这样的关系：

\[\left(AA^*\right) A\mathbf{v_i} = \lambda_i A \mathbf{v_i}\\ \]

再写一遍：

\[\left(AA^*\right) \left(A\mathbf{v_i}\right) = \lambda_i \left(A\mathbf{v_i}\right)\\ \]

看出来了吗？这不明摆着说： \(A\mathbf{v_i}\) 是 \(W\) 上正算子 \(AA^*\) 的特征向量嘛！

如果我们对 \(AA^*\) 在 \(m\) 个单位正交的特征向量 \(\mathbf{u}_{1}, \ldots, \mathbf{u}_{m}\) 上进行分解，并且对特征值也进行有序排列，有：

\[\begin{aligned} \left(A A^{*} \right) \mathbf{u}_{i}&=\lambda_{i} \mathbf{u}_{i}, \quad \ 1 \leq i \leq r \\ A A^{*} \mathbf{u}_{i}&=\mathbf{0} , \quad r+1 \leq i \leq m \end{aligned}\\ \]

对比这两个式子：

\[\begin{aligned} \left(AA^*\right) \left(A\mathbf{v_i}\right) &= \lambda_i \left(A\mathbf{v_i}\right) \\ \left(A A^{*} \right) \mathbf{u}_{i} &= \lambda_{i} \mathbf{u}_{i} \end{aligned}\\ \]

说明 \(A\mathbf{v_i}\) 和 \(\mathbf{u_i}\) 只是“长度”不相等，相差一个倍数，这个倍数就是 \(Av_i\) 的内积范数：

\[\langle{ A\mathbf{v_i} \,, A\mathbf{v_i} }\rangle = \left( A\mathbf{v_i} \right)^* A\mathbf{v_i} = \mathbf{v_i}^*A^*A\mathbf{v_i} = \sigma_i^2 \mathbf{v_i}^*\mathbf{v_i} = \sigma_i^2\\ \]

所以 \(A\mathbf{v_i}\) 的范数为：

\[\Vert A\mathbf{v_i} \Vert = \sqrt{ \langle{ A\mathbf{v_i} \,, A\mathbf{v_i} }\rangle } = \sigma_i\\ \]

恰恰就为 \(\sigma_i\) ，我们称这个正实数为 \(A\) 的奇异值，一共有 \(r\) 个。显然：

\[A\mathbf{v_i} = \sigma_i \mathbf{u_i}\\ \]

我们前面贪婪的愿望真的被实现了。 \(\blacksquare\)

线性映射的奇异值分解——矩阵形式的推导(SVD)

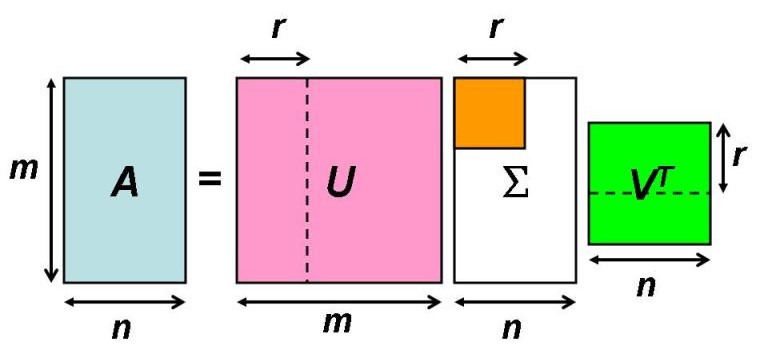
image

令 \(U=\left[\begin{array}{lll}\mathbf{u}_{1} & \cdots & \mathbf{u}_{m}\end{array}\right]\) ， \(V=\left[\begin{array}{lll}\mathbf{v}_{1} & \cdots & \mathbf{v}_{n}\end{array}\right]\) 。由于 \(A^*A\) 在 \(\mathbf{v}_{1}, \ldots, \mathbf{v}_{n}\) 下进行了谱分解， \(AA^*\) 在 \(\mathbf{u}_{1}, \ldots, \mathbf{u}_{m}\) 下进行了谱分解，那么谱定理告诉我们，矩阵 \(U=\left[\begin{array}{lll}\mathbf{u}_{1} & \cdots & \mathbf{u}_{m}\end{array}\right]\) 和 \(V=\left[\begin{array}{lll}\mathbf{v}_{1} & \cdots & \mathbf{v}_{n}\end{array}\right]\) 都是酉矩阵， \(U^{*} U = U U^{*} = I_{m}\) 且 \(V^{*} V = V V^{*} = I_{n}\) 。

\[\begin{aligned} A V &=A\left[\begin{array}{lll} \mathbf{v}_{1} & \cdots & \mathbf{v}_{n} \end{array}\right] \\ &=\left[\begin{array}{lll} A \mathbf{v}_{1} & \cdots & A \mathbf{v}_{n} \end{array}\right] \\ &=\left[\begin{array}{lllll} \sigma_{1} \mathbf{u}_{1} & \cdots & \sigma_{r} \mathbf{u}_{r} & \mathbf{0} & \cdots & \mathbf{0} \end{array}\right] \\ &=\left[\begin{array}{llll} \mathbf{u}_{1} & \cdots & \mathbf{u}_{m} \end{array}\right]\left[\begin{array}{ccc|c} \sigma_{1} & & & \\ & \ddots & & 0 \\ & & \sigma_{r} & \\ \hline & 0 & & 0 \end{array}\right] \\ &=U \Sigma . \end{aligned}\\ \]

两边右乘 \(V^{*}\) ，得：

\[A=U \Sigma V^{*}\\ \]

这就是线性映射的奇异值分解 SVD 的完整矩阵表达形式。 \(\blacksquare\)

结语 Epilogue

我们的本意是在 \(V\) 和 \(W\) 中各自找到一组基，使得同构关系： \(\operatorname{range}{A}^* \cong \operatorname{range}{A}\) 在这组基下有最清晰的线性表达，惊人的巧合就在这里，在对 \(A^*A\) 和 \(AA^*\) 进行谱分解的分析过程中，发现 \(A^*A\) 的 \(n\) 个单位正交特征向量 \(\mathbf{v}_{1}, \ldots, \mathbf{v}_{n}\) 若作为 \(V\) 中的一组基， \(AA^*\) 的 \(m\) 个单位正交特征向量 \(\mathbf{u}_{1}, \ldots, \mathbf{u}_{m}\) 若作为 \(W\) 中的一组基，恰恰满足上面的这个线性表达条件！且进一步发现只有 \(r\) 个向量之间的一一映射是实际在起作用的，或者说是“有效”的。那些 \(n-r\) 个特征值为 \(0\) 的向量 \(\mathbf{v}_{r+1}, \ldots, \mathbf{v}_{n}\) 被 \(A\) 映射到 \(W\) 中的 \(\mathbf{0}\) ， \(m-r\) 个特征值为 \(0\) 的向量 \(\mathbf{u}_{r+1}, \ldots, \mathbf{u}_{m}\) 被 \(A^*\) 映射到 \(V\) 中的 \(\mathbf{0}\) 。多么清晰明了，也和我们脑中的直观理解相吻合。

预告 Future

下一讲我会讲述一下不同于代数线性代数，数值线性代数中的 SVD 如何得到以及 SVD 的几个具体应用，这一部分的内容源自于前段时间看到的一份讲义（Computer Science Theory for the Information Age, Spring 2012.）。

posted @ 2021-11-14 17:41  夏小正的鲜小海  阅读(374)  评论(0)  编辑  收藏  举报