可持久化线段树学习笔记
大概内容：可持久化线段树，可持久化并查集。
待填坑，预计在10.12之前写完。
主席树解决的问题是当一类数据结构要保存历史版本时，普通线段树、平衡树等无法保存历史版本。当前节点更新之后历史版本就被覆盖了。
我们当然可以考虑对于每一次操作建一棵线段树，到时候直接查询就可以了。但这样时空复杂度均是 \(n^2\) 的。
如何优化？
我们考虑这样一个图
假设我们修改了 \(5\) 的值，那么发现，受影响的会是标红的这一条链。
也就是说我们建树的时候不需要建整棵线段树，只需要新建一部分记录这次修改即可。如图。
粉色的时新建出来那部分。即被影响的单独建点，没被影响的直接连边。
然后每次查询的时候找到历史版本对应的那棵树，直接查询即可。
但是这个只支持单点修改，单点查询。区间修改，区间查询要打懒标记，但懒标记要永久化比较麻烦，我还不会。
先放代码吧，单点修改，单点查询。
struct ZXTREE{
int T[N];
int ini[N];
int ls[N<<5];
int rs[N<<5];
int val[N<<5];
int cnt;
int build(int l,int r)
{
int rt=++cnt;
if(l==r)
{
val[rt]=ini[l];
return rt;
}
int mid=(l+r)>>1;
ls[rt]=build(l,mid);
rs[rt]=build(mid+1,r);
return rt;
}
int change(int ver,int l,int r,int id,int k)
{
int rt=++cnt;
ls[rt]=ls[ver];
rs[rt]=rs[ver];
if(l==r)
{
val[rt]=k;
return rt;
}
int mid=(l+r)>>1;
if(id<=mid)
{
ls[rt]=change(ls[ver],l,mid,id,k);
}
else
{
rs[rt]=change(rs[ver],mid+1,r,id,k);
}
return rt;
}
int query(int rt,int l,int r,int id)
{
if(l==r)
{
return val[rt];
}
int mid=(l+r)>>1;
if(id<=mid)
{
return query(ls[rt],l,mid,id);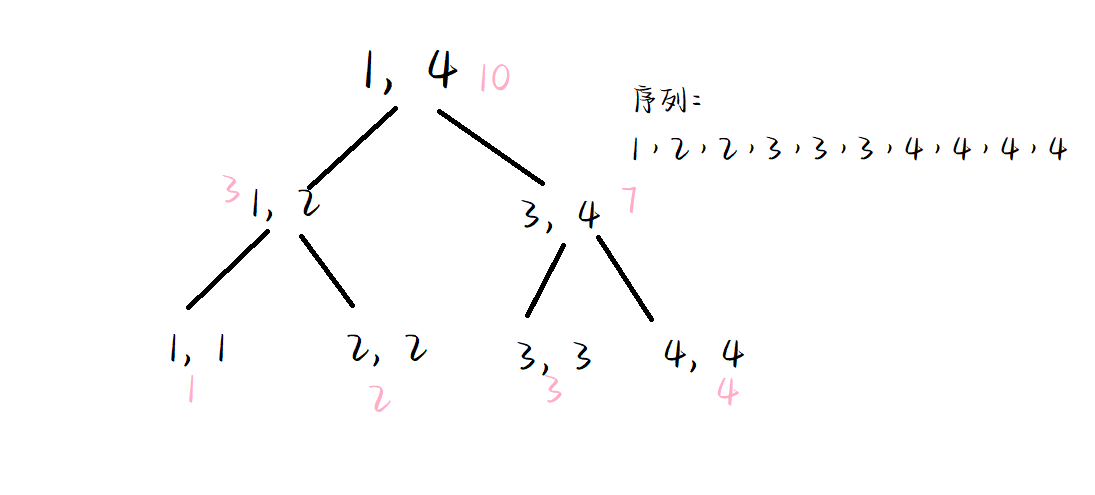
}
else
{
return query(rs[rt],mid+1,r,id);
}
}
}tree;
还有一个经典问题，区间第 \(k\) 小。
首先考虑整段区间第 \(k\) 小怎么做。引入一个概念，值域线段树。即下标是值域的线段树。
我们先离散化原数组，然后根据值域建一棵线段数，对于每个叶节点，维护一下这个值在原序列的出现次数。对于非叶节点，维护这个值域内的元素个数。
例如以下数组 \(1,2,2,3,3,3,4,4,4,4\) 建出来的值域线段数如下。
其中粉色的表示这个数的出现次数。而紫色的表示这个值域内的元素个数。
下面来不及写了，先复制了，记得自己重写一份。
容易发现，值域线段树可以查 \(1~r\) 的第 \(k\) 大但是无法查询区间的。具体原因是无法确定具体位置。
所以我们考虑可持久化一下，假设原数组有 \(n\) 个数则建立一个有 \(n\) 个根的可持久化值域线段树，对于每一个区间，设当前根为 \(i\) ，维护一个值表示在原数组中 \([1,i]\) 的数的个数。看图理解会好一点。
我们要找 \([1,r]\) 的第 \(k\) 小过程是这样的。
-
先找到编号为 \(r\) 的那个根。
-
向下递归，如果左节点的个数 \(x\le k\) 就一定在右子树，否则在左子树，继续往下递归。但是若 \(x\le k\) 向右子树递归时就证明范围已经从 \([1,r]\) 变成了 \([x+1,r]\) 所以问题变成了在 \([x+1,r]\) 中寻找第 \(k-x\) 大的数。
例如我们查找 \([1,4]\) 中第 \(2\) 小的值，图示如下，绿色节点为该值存在的区间位置。
struct ZXTREE{
int T[N];
int ini[N];
int ls[N<<5];
int rs[N<<5];
int val[N<<5];
int sum[N<<5];
int cnt;
int build(int l,int r)
{
int rt=++cnt;
if(l==r)
{
val[rt]=ini[l];
return rt;
}
int mid=(l+r)>>1;
ls[rt]=build(l,mid);
rs[rt]=build(mid+1,r);
return rt;
}
int change(int ver,int l,int r,int id)
{
int rt=++cnt;
ls[rt]=ls[ver];
rs[rt]=rs[ver];
sum[rt]=sum[ver]+1;
if(l==r)
{
// val[rt]=k;
return rt;
}
int mid=(l+r)>>1;
if(id<=mid)
{
ls[rt]=change(ls[ver],l,mid,id);
}
else
{
rs[rt]=change(rs[ver],mid+1,r,id);
}
return rt;
}
int query(int u,int v,int l,int r,int id)
{
if(l==r)
{
return l;
}
int mid=(l+r)>>1;
int x=sum[ls[v]]-sum[ls[u]];
if(x>=id)
{
return query(ls[u],ls[v],l,mid,id);
}
else
{
return query(rs[u],rs[v],mid+1,r,id-x);
}
}
}ans;
可持久化并查集。
可持久化并查集实际上就是用主席树维护并查集的 \(fa_i\) 数组。
不过由于可持久化了，所以路径压缩是不成立的。所以采用按秩合并或启发式合并来实现复杂度。
具体地，建立两棵可持久化线段树，\(fa\) 和 \(sz\) 分别表示每个点的父亲和大小。每次合并的时候查询一下 \(a\) 和 \(b\) 的大小，也就是单点查询。之后把小的合并到大的即可，也就是单点修改。
代码：
int findrt(int x,int ver)
{
while(fa.query(fa.T[ver],1,n,x)!=x)x=fa.query(fa.T[ver],1,n,x);
return x;
}
void merge(int x,int y,int ver)
{
int a=findrt(x,ver);
int b=findrt(y,ver);
if(a==b) return ;
int szx=sz.query(sz.T[ver],1,n,a);
int szy=sz.query(sz.T[ver],1,n,b);
if(szx<szy)
{
fa.T[ver]=fa.change(fa.T[ver],1,n,a,b);
sz.T[ver]=sz.change(sz.T[ver],1,n,b,szx+szy);
}
else
{
fa.T[ver]=fa.change(fa.T[ver],1,n,b,a);
sz.T[ver]=sz.change(sz.T[ver],1,n,a,szx+szy);
}
}
