哇!树链剖分(重链剖分学习笔记)
听说有人不会树链剖分?
前置芝士
- 线段树
- 树状数组
- Splay
- FHQ-Treap
以上五种任意一种即可,这里主要讲线段树做法。
引入
树链剖分(Tree Line Pow Divide),一种解决树上快速路径修改查询问题的算法,一般指 重链剖分(Heavy Path Decomposition)。
思想图解
一个问题
如题,已知一棵包含
-
1 x y z,表示将树从 -
2 x y,表示求树从
一些定义
顾名思义,重链剖分就是把”重“的链与其他的链分开,那么如何定义重呢?
我们定义一个 重儿子(Heavy Son)的概念:
以该点的儿子为根的子树中节点个数最多的儿子为重儿子
那么就可以递归定义 重链:
若节点 u 为节点 v 的重儿子,那么 v 就归入到 u 所在的链中
否则,节点 v 就单独成为一条链的链首
那么一棵树可以被剖成这个样子:
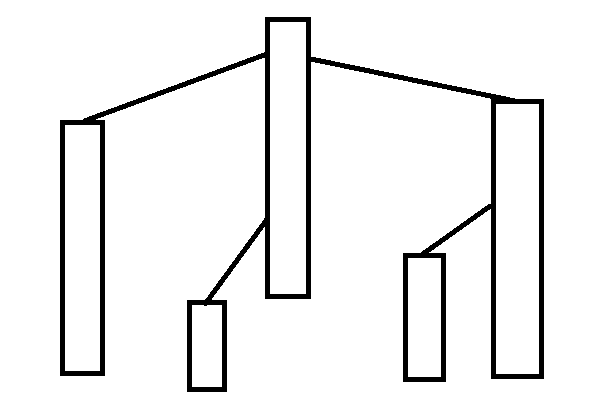
其中一个长方形代表一条链。
接下来即可定义一个 链顶 的概念:
一条链中,深度最低的点
深度,即
根节点到该节点的距离+1
思想概述
看到类似区修区查的语言:
-
所有节点的值都加上
-
所有节点的值之和。
不难想到用线段树(或树状数组等,下同);
但是难想的就是如何将一棵树剖成一个序列,从而使用线段树呢?
我们可以将树中的的节点重新编号,按照编号顺序建线段树,
其中编号序列满足以下条件(先不说为什么,待会再讲):
所有的重链的编号是连续的
是一种dfs序
这里我不想画图了,读者自己体会。
可以建树了,但是修改查询还不会。
修改
我们先考虑一种简单的情况:
情况A
修改的两个点 A,B 在同一条重链上:
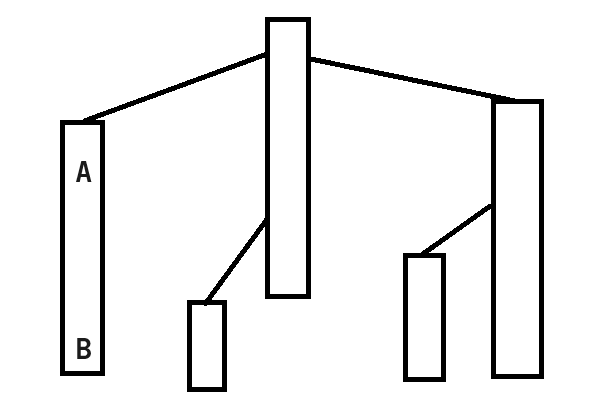
根据我们dfs序的建立,易证 A 到 B 的路径上的节点在线段树上一定是连续的。
那么就可以通过线段树的区间修改操作实现了。
这里就可以填上我刚才挖的那个坑了。
情况B
再引入一下
一个很好理解的定理(废话):
任意一个链顶不为根的链,链顶的父亲一定是另外一条链的一部分
同样,这里我不想画图了,读者自己体会。
接下来要讨论的情况就是不在同一条链上:
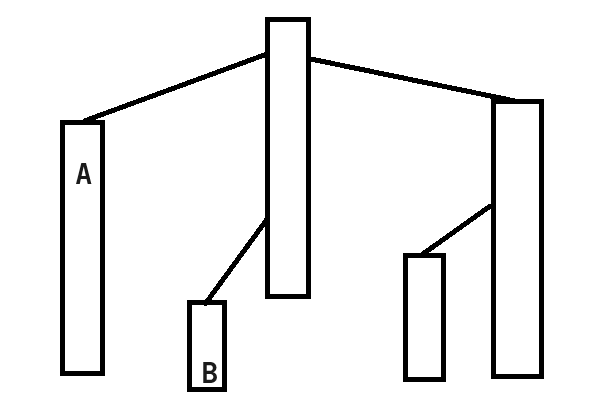
我们可以先把链顶深度较低的 B 所在的这条链的所有点修改了,并跳到其链顶的父亲所在的链的最后一个节点上;
接着同理修改 A;
即每次将链顶深度较低的往上爬,直到 A 与 B 重合。
其实,可以将两者结合一下:
每次将链顶深度较低的往上爬,直到 A 与 B 在同一条链。
施行情况A(因为 A 与 B 在同一条链上并不意味着 A = B)
查询
与修改大同小异,只是把
代码
模板题 洛谷 P3384 【模板】重链剖分/树链剖分
int a[Maxn], tmp[Maxn];
int p;
struct SegmentTree {//线段树
#define ls (id << 1)
#define rs (id << 1 | 1)
struct Segment {
int Left;
int Right;
int valMax;
int tag;
int valSum;
} seg[Maxn << 2];
il void PushUp(int id) {
seg[id].valMax = max(seg[ls].valMax, seg[rs].valMax) % p;
seg[id].valSum = (seg[ls].valSum + seg[rs].valSum) % p;
return;
}
il void PushDown(int id) {
if (seg[id].tag) {
seg[ls].tag += seg[id].tag;
seg[ls].tag %= p;
seg[ls].valSum += seg[id].tag * (seg[ls].Right - seg[ls].Left + 1);
seg[ls].valSum %= p;
seg[rs].tag += seg[id].tag;
seg[rs].tag %= p;
seg[rs].valSum += seg[id].tag * (seg[rs].Right - seg[rs].Left + 1);
seg[rs].valSum %= p;
seg[id].tag = 0;
}
return;
}
il void Build(int id, int Left, int Right) {
seg[id] = {Left, Right, 0, 0, 0};
if (Left == Right) {
seg[id].valMax = a[Left] % p;
seg[id].valSum = a[Left] % p;
return;
}
int mid = (Left + Right) >> 1;
Build(ls, Left, mid);
Build(rs, mid + 1, Right);
PushUp(id);
return;
}
il int QuerySum(int id, int Left, int Right) {
PushDown(id);
if (seg[id].Right < Left || seg[id].Left > Right) {
return 0;
}
if (Left <= seg[id].Left && seg[id].Right <= Right) {
return seg[id].valSum % p;
}
return (QuerySum(ls, Left, Right) + QuerySum(rs, Left, Right)) % p;
}
il void Change(int id, int Left, int Right, int val) {
PushDown(id);
if (seg[id].Right < Left || seg[id].Left > Right) {
return;
}
if (seg[id].Left >= Left && Right >= seg[id].Right) {
seg[id].tag += val;
seg[id].tag %= p;
seg[id].valSum += val * (seg[id].Right - seg[id].Left + 1) % p;
seg[id].valSum %= p;
return;
}
Change(ls, Left, Right, val);
Change(rs, Left, Right, val);
PushUp(id);
return;
}
};//以上内容不做解释
vector<int> G[Maxn];//邻接表
int n, m, root;
struct Qtree {//重链剖分
struct treeNode {
int fa;//该节点的父亲
int son;//重儿子
int dep;//深度
int size;//字数节点个数
int top;//该点所在链的链顶
int tid;//重新编号的序号
} tn[Maxn];
SegmentTree SEG;
int tot = 0;
void dfs1(int step, int fa) {//初始化fa、dep、size、son
tn[step].fa = fa;
tn[step].dep = tn[fa].dep + 1;
tn[step].size = 1;
int Max = 0;
for (auto x : G[step]) {
if (x == fa) {
continue;
}
dfs1(x, step);
tn[step].size += tn[x].size;
if (tn[x].size > Max) {//判重儿子
Max = tn[x].size;
tn[step].son = x;
}
}
return;
}
void dfs2(int step, int top) {//初始化top、tid
tn[step].top = top;
tn[step].tid = ++tot;//有没有像Tarjan的dfn?
a[tot] = tmp[step];//重新将点权赋值
if (tn[step].son)//避免死循环
dfs2(tn[step].son, top);//重儿子
for (auto x : G[step]) {
if (x == tn[step].fa || x == tn[step].son) {//排除重儿子
continue;
}
dfs2(x, x);//因为x不是重儿子,所以x所在链的链首为自己
}
}
void Build() {//建立
dfs1(root, 0);//以root为根dfs
dfs2(root, root);
SEG.Build(1, 1, n);//以a数组建立线段树
return;
}
void Change(int u, int v, int w) {
while (tn[u].top != tn[v].top) {//u,v不在同一条链上
if (tn[tn[u].top].dep < tn[tn[v].top].dep) {//简洁写法,即把链顶深度较低的点放到u
swap(u, v);
}
SEG.Change(1, tn[tn[u].top].tid, tn[u].tid, w % p);//修改
u = tn[tn[u].top].fa;//往上爬
}
if (tn[u].tid > tn[v].tid) {//最后执行情况A
swap(u, v);
}
SEG.Change(1, tn[u].tid, tn[v].tid, w % p);
return;
}
int QuerySum(int u, int v) {//同理
int Max = 0;
while (tn[u].top != tn[v].top) {
if (tn[tn[u].top].dep < tn[tn[v].top].dep) {
swap(u, v);
}
Max += SEG.QuerySum(1, tn[tn[u].top].tid, tn[u].tid);
Max %= p;
u = tn[tn[u].top].fa;
}
if (tn[u].tid > tn[v].tid) {
swap(u, v);
}
return Max + SEG.QuerySum(1, tn[u].tid, tn[v].tid);
}
} Qt;
最后读者可以自行思考一下如何将边权转成点权,洛谷 P4114 Qtree1。
THE END
感谢 @Little_Cabbege、@qw1234321、@yinxiangbo2027 指出了本文的一些问题。



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 一个费力不讨好的项目,让我损失了近一半的绩效!
· 清华大学推出第四讲使用 DeepSeek + DeepResearch 让科研像聊天一样简单!
· 实操Deepseek接入个人知识库
· CSnakes vs Python.NET:高效嵌入与灵活互通的跨语言方案对比
· Plotly.NET 一个为 .NET 打造的强大开源交互式图表库