赫夫曼\哈夫曼\霍夫曼编码 (Huffman Tree)

哈夫曼树
给定n个权值作为n的叶子结点，构造一棵二叉树，若带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

哈夫曼编码(Huffman Coding)

又称霍夫曼编码，是一种编码方式，哈夫曼编码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法，该方法完全依据字符出现概率来构造异字头的平均长度最短的码字，有时称之为最佳编码，一般就叫做Huffman编码（有时也称为霍夫曼编码）。

应用举例

哈夫曼树─即最优二叉树，带权路径长度最小的二叉树，经常应用于数据压缩。 在计算机信息处理中，“哈夫曼编码”是一种一致性编码法（又称“熵编码法”），用于数据的无损耗压缩。这一术语是指使用一张特殊的编码表将源字符（例如某文件中的一个符号）进行编码。这张编码表的特殊之处在于，它是根据每一个源字符出现的估算概率而建立起来的（出现概率高的字符使用较短的编码，反之出现概率低的则使用较长的编码，这便使编码之后的字符串的平均期望长度降低，从而达到无损压缩数据的目的）。

构造Huffman tree

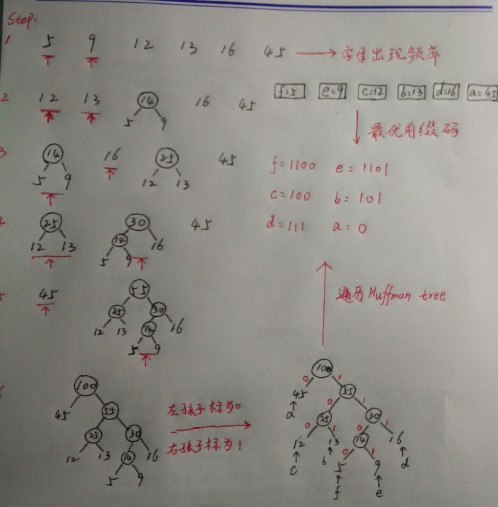
过程：

1、输入字符关键字以及对应的频率。

2、根据关键字的频率构造最优二叉树

　　(1)借助于STL的优先队列 ：priority_queue<type, vector<type>,cmp>que; 其中type为优先队列的类型，比如说int, double, 也可以将结构体作为类型。vector它是一个多功能的，能够操作多种数据结构和算法的模板类和函数库。借助于vector可以很轻松的解决一些问题。cmp为定义的优先队列的出队规则，给出博客http://www.cnblogs.com/buptLizer/archive/2011/09/11/2173708.html大家可以参考来理解优先队列的使用。以及其中常用的操作que.pop(), que.push(), que.top(), que.size()等...

　　(2)构造最优二叉搜索树：在有了最优二叉搜索树的帮助之后，对于构建搜索树很容易。上面的图很清楚的讲解了构造的过程，每次取出频率最小的两个形成一个子树，将其频率相加之后再放入优先队列之中，直到队列中元素个数为0。在操作过程中需要遵守最优二叉搜索树的定义，左孩子小于父节点，右孩子大于父节点。

　　(3)递归遍历二叉树：遍历中只需要记住，向左遍历那么前缀码为0,向右为1.

亲测代码：

#include <bits/stdc++.h>
#define max_size 10010
char c[max_size];
double f[max_size];

using namespace std;
typedef struct node
{
    char ch;
    double freq;
    node *lchild;
    node *rchild;
    node(char c=0,double f=0,node *l=NULL,node *r=NULL):
        ch(c),freq(f),lchild(l),rchild(r) {}
};
typedef struct cmp
{
    bool operator()(node*&a,node*&b)
    {
        return a->freq>b->freq;
    }
};
node* createTree(int n)
{
    priority_queue<node*,vector<node*>,cmp>que;
    for(int i=1; i<=n; i++)
    {
        cin>>c[i]>>f[i];
        que.push(new node(c[i],f[i]));
    }
    while(que.size()>1)
    {
        node *l=que.top();
        que.pop();
        node *r=que.top();
        que.pop();
        node *newnode=new node(0,l->freq+r->freq,l,r);
        que.push(newnode);
    }
    return que.top();
}

void printInfo(const node *tree,string code)
{
    if(tree->lchild==NULL&&tree->rchild==NULL)
    {
        cout<<tree->ch<<":"<<code<<"  ";
        return;
    }
    if(tree->lchild!=NULL)printInfo(tree->lchild,code+'0');
    if(tree->rchild!=NULL)printInfo(tree->rchild,code+'1');
}
void deleteTree(node *tree)
{
    if(tree->lchild!=NULL)deleteTree(tree->lchild);
    if(tree->rchild!=NULL)deleteTree(tree->rchild);
    delete(tree);
}
int main()
{
    int n;
    priority_queue<node*,vector<node*>,greater<node*> >que;
    while(~scanf("%d",&n))
    {
        node *tree=createTree(n);
        printf("Huffman code:\n");
        printInfo(tree,"");
    }
}

输入数据以及运行结果: