Pytorch框架学习---（1）张量操作

该系列是本人学习【深度之眼Pytorch框架训练营】的相关笔记，每一节的内容，随着后续编写代码慢慢更新，仅供参考。

注：【深度之眼训练营】个人认为作为系统性入门学习AI领域还是较好的，该平台课程由浅入深，系统性较强，值得购买学习！

深度之眼公众号

[本文来自博客steven_zhao1001],转载请注明来源，谢谢配合！

一. 张量
二. 自动求导autograd

一. 张量

1.张量定义

张量我们可以理解为是一个多维数组，即标量、向量、矩阵的高维拓展。

标量：0维张量
向量：1维张量
矩阵：2维张量

注意：

out = torch.tensor(data=[1])  # out为一维张量：向量，并不是标量
out = torch.tensor(data=1)  # out为标量

2.torch.Tensor封装

自pytorch0.4.0之后，Variable被封装到Tensor内，即：

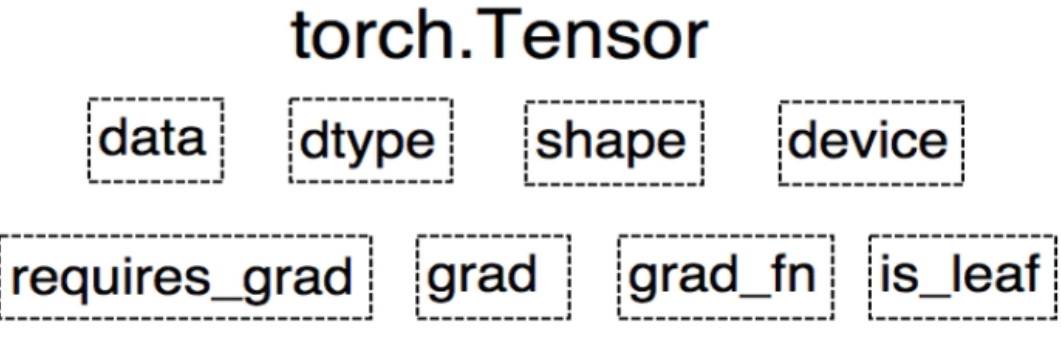
torch.Tensor封装

其中：

data: 被包装的Tensor，
dtype：张量的数据类型，如 torch.float，
device：CPU/GPU，
requires_grad：判断是否需要梯度，
grad：data的梯度，
grad_fn：获得该tensor的function方法，用于自动求导，
is_leaf：判断该变量是否为叶子节点（初始设置的变量，如x,w,其中y=x*w不是叶子节点）。

3.张量的创建

（1）直接创建

b = torch.tensor(data)
a = torch.from_numpy(ndarry)  # 由numpy创建转为Tensor，改变a的内容也会改变ndarry，但是id() 地址不同（类似指针操作）

（2）根据给定数值

例如：

torch.zeros()  # 依据size创建 全0 张量
torch.ones()  # 全1张量
torch.full()  # 依据给定value值，创建全value的张量
torch.arange()  # 根据start、end、step，创建等差张量 [start, end) 
torch.eye()  # 创建单位对角矩阵I

（3）根据概率分布

例如：

# 正太分布
a = torch.normal(mean，std，out=None，size=None)  # 根据mean和std创建正态分布，其中 1.out参数为：将a赋予out变量；2.当mean，std都为标量时，设置size
torch.randn()  # 依据size创建标准正态分布
# 均匀分布
torch.rand()  # [0，1）均匀分布
torch.randint(low，high)  # [low, high)整数均匀分布
# 一维张量随机排列
torch.randperm(n)  # 创建0到n-1的随机排列

4.张量操作

（1）拼接

torch.cat(dim)  # 不扩展维度，按照dim进行拼接，如：2个2维张量（2, 3），dim=0 --》（4,3）
torch.stack(dim)  # 扩展维度, 在新建的dim上进行拼接，如：2个2维张量（1, 3），dim=2 --》（1,3,2）

（2）切分

torch.chunck(data, dim, chunck)  # 按dim，将data切chunck份，如2维张量（2, 7），dim=1 --》（2, 3）、（2, 3）、（2, 1）
torch.split(tensor, dim, split_size_or_sections)  # 当后面参数为int，即切分的长度；当参数为list，则依次将list中元素作为每一份长度

（3）索引

torch.index_select(input, dim, index)  # 沿dim，根据给定的index序号，索引input内容, 其中index必须是torch.long，如：
      a=torch.tensor([[4,5,6],[1,2,3],[3,4,5]]) # a.shape = (3,3)
      out = torch.index_select(a, dim=0, index=[0, 2])  # out = [[4,5,6], [3,4,5]]
torch.masked_select(input, mask)  # mask为布尔类型， 根据mask中True位置，选取data，依次输出 1维 张量

（4）变换

torch.reshape(input, shape)  # 根据新size重新排列input，*注意*：例如shape=（-1，2），-1位置由系统自动计算； reshape之后共享内存
torch.transpose(input, dim0, dim1)  # 交换张量的两个维度

# transpose只能转换两个维度，而tensor.permute(a,b,c,d, )可以对任意高维矩阵变换维度，注意没有torch.permute用法

torch.t(input)  # 针对2维张量的转置
torch.squeeze(input, dim=None)  # 压缩长度为1的维度（轴） 或 压缩指定维度dim（当且仅当该维度长度为1）
torch.unsqueeze(input, dim)  # 依据dim扩展维度（长度为1）

（5）数学运算

这里有很多种数学运算，例如最基本的加add减sub乘mul除div，次方pow、绝对值abs等，可查看pytorch官方文档

# 列举一个特殊函数，类似的还有torch.addcdiv、torch.addcmul
torch.add(input, alpha=1, other, out=None)  # out = input + alpha *other 逐元素
torch.bmm(a,b)  # 针对三维张量的矩阵乘法运算

二. 自动求导autograd

torch.autograd.backward(tensors,retain_graph=None, Create_graph=False, grad_tensor=None)
# retain_graph:是否保留该节点梯度；Create_graph：创建导数的计算图，用于计算高阶导； grad_tensor：有多个梯度组合时，设置各梯度权重