排序---优先队列
写在前面的话:
一枚自学Java和算法的工科妹子。
- 算法学习书目:算法(第四版) Robert Sedgewick
- 算法视频教程:Coursera Algorithms Part1&2
本文是根据《算法(第四版)》的个人总结,如有错误,请批评指正。
一、优先队列介绍
优先队列是0个或多个元素的集合,每个元素都有一个优先权或值,对优先队列执行的操作有1) 插入元素;2) 删除最大(最小)元素.
在最小优先队列(min priority queue)中,删除操作用来删除优先权最小的元素;在最大优先队列(max priority queue)中,删除操作用来删除优先权最大的元素。
优先队列的使用和队列(删除最老的元素)以及栈(删除最新的元素)类似,但高效的实现它则更具有挑战性。
优先队列是一种抽象数据类型,它表示了一组值和对这些值的操作。优先队列(最大优先队列为例)的API设计如下:

设计优先队列API,我们想实现的功能:输入N个字符串(N非常大),每个字符串都对应着一个整数,目标就是从中找出最大的(或最小的)M个整数及其关联的字符串。在上述API中着重要关注的方法就是插入insert()和删除最大元素delMax().
解决方法:
1.将输入排序然后从中找出M个最大的元素,但是因为输入元素非常庞大,造成存储空间的浪费;
2.将每个新的输入和已知的M个最大元素对比,这会导致比较的时间复杂度为NM;
3.以下会介绍基于堆的优先队列实现,降低时间和空间复杂度。
表1 从N个输入中找到最大的M个元素所需的成本
| 示 例 | 时间复杂度 | 空间复杂度 |
| 排序算法的用例(方法一) | NlgN | N |
| 初级实现的优先队列(方法二) | NM | M |
| 基于堆的优先队列(方法三) | NlgM | M |
优先队列的初级实现:
1.数组实现(无序)
- 插入操作:和栈的push()方法完全一样;
- 删除操作:添加一段类似于选择排序的内循环,将最大元素和边界元素交换,然后删除,和pop()操作一样;
1 public class UnorderedMaxPQ<Key extends Comparable<Key>> 2 { 3 private Key[] pq; // pq[i] = ith element on pq 4 private int N; // number of elements on pq 5 6 public UnorderedMaxPQ(int capacity){ 7 pq = (Key[]) new Comparable[capacity]; 8 } 9 10 public boolean isEmpty(){ return N == 0; } 11 12 public void insert(Key x){ pq[N++] = x; } 13 14 public Key delMax(){ 15 int max = 0; 16 for (int i = 1; i < N; i++) 17 if (less(max, i)) max = i; 18 exch(max, N-1); 19 return pq[--N]; 20 } 21 }
2.数组实现(有序)
- 插入操作:将所有较大的元素向右边移动一个使数组保持有序,类似于插入排序;
- 删除操作:和栈的pop()操作一样;
表2 优先队列的各种事先在最坏情况下运行时间的增长数量级
| 数据结构 | 插入元素 | 删除最大元素 |
| 无序数组 | N | 1 |
| 有序数组 | 1 | N |
| 堆 | lgN | lgN |
二、二叉堆的介绍
在二叉堆数组中,每个元素都要保证大于等于另两个特定位置的元素。从a[k]向上一层就令k=k/2,向下一层就令K=2k或2k+1。一颗大小为N的完全二叉树的高度为lgN向下取整。
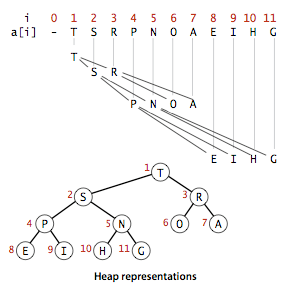
堆有序化操作:
(1)由下至上的堆有序化(上浮)
1 private void swim(int k) { 2 while (k > 1 && less(k/2, k)) { 3 exch(k, k/2); 4 k = k/2; 5 } 6 }
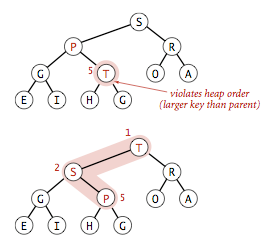
(2)由上至下的堆有序化(下沉)
1 private void sink(int k) { 2 while (2*k <= N) { 3 int j = 2*k; 4 if (j < N && less(j, j+1)) j++; 5 if (!less(k, j)) break; 6 exch(k, j); 7 k = j; 8 } 9 }
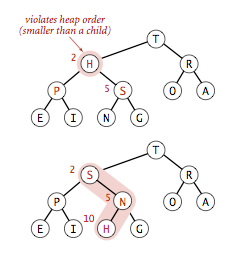
三、基于堆的优先队列
1.如何实现?
- 优先队列有一个基于堆的完全二叉树表示,存储于数组pq[1..N]中,pq[0]没有使用。
- 在insert()中,我们将N加1并把新元素添加在数组最后,然后用swim()恢复堆的秩序。
- 在delete()中,我们从pq[1]中得到需要的返回元素,然后将pq[N]移动到pq[1],将N减1并使用sink()恢复堆的秩序。
- 同时我们还将不在使用的pq[N+1]设置为null,以便系统回收删除元素所占用的空间,也使用了动态调整数组大小的方法,具体见下压栈(LILO)详解。
2.性能分析
对于一个含有N个元素的基于堆的优先队列,插入元素操作只需不超过(lgN+1)次比较,删除最大元素的操作需要不超过2lgN次比较,以下是代码实现:
1 import java.util.Comparator; 2 import java.util.Iterator; 3 import java.util.NoSuchElementException; 4 5 public class MaxPQ<Key> implements Iterable<Key> { 6 private Key[] pq; // 完全二叉树 7 private int n; // 优先队列中元素数目 8 private Comparator<Key> comparator; // optional Comparator 9 10 public MaxPQ(int initCapacity) { 11 pq = (Key[]) new Object[initCapacity + 1]; 12 n = 0; // pq[0]没有使用 13 } 14 15 public MaxPQ() { this(1);} 16 17 public MaxPQ(int initCapacity, Comparator<Key> comparator) { 18 this.comparator = comparator; 19 pq = (Key[]) new Object[initCapacity + 1]; 20 n = 0; 21 } 22 23 public MaxPQ(Comparator<Key> comparator) { 24 this(1, comparator); 25 } 26 27 public MaxPQ(Key[] keys) { 28 n = keys.length; 29 pq = (Key[]) new Object[keys.length + 1]; 30 for (int i = 0; i < n; i++) 31 pq[i+1] = keys[i]; 32 for (int k = n/2; k >= 1; k--) 33 sink(k); 34 assert isMaxHeap(); 35 } 36 37 public boolean isEmpty() {return n == 0; } 38 39 public int size() {return n;} 40 41 public Key max() { 42 if (isEmpty()) throw new NoSuchElementException("Priority queue underflow"); 43 return pq[1]; 44 } 45 46 private void resize(int capacity) { 47 assert capacity > n; 48 Key[] temp = (Key[]) new Object[capacity]; 49 for (int i = 1; i <= n; i++) { 50 temp[i] = pq[i]; 51 } 52 pq = temp; 53 } 54 55 public void insert(Key x) { 56 57 // double size of array if necessary 58 if (n >= pq.length - 1) resize(2 * pq.length); 59 60 // add x, and percolate it up to maintain heap invariant 61 pq[++n] = x; 62 swim(n); 63 assert isMaxHeap(); 64 } 65 66 public Key delMax() { 67 if (isEmpty()) throw new NoSuchElementException("Priority queue underflow"); 68 Key max = pq[1]; 69 exch(1, n--); 70 sink(1); 71 pq[n+1] = null; // to avoid loiterig and help with garbage collection 72 if ((n > 0) && (n == (pq.length - 1) / 4)) resize(pq.length / 2); 73 assert isMaxHeap(); 74 return max; 75 } 76 77 private void swim(int k) { 78 while (k > 1 && less(k/2, k)) { 79 exch(k, k/2); 80 k = k/2; 81 } 82 } 83 84 private void sink(int k) { 85 while (2*k <= n) { 86 int j = 2*k; 87 if (j < n && less(j, j+1)) j++; 88 if (!less(k, j)) break; 89 exch(k, j); 90 k = j; 91 } 92 } 93 94 private boolean less(int i, int j) { 95 if (comparator == null) { 96 return ((Comparable<Key>) pq[i]).compareTo(pq[j]) < 0; 97 } 98 else { 99 return comparator.compare(pq[i], pq[j]) < 0; 100 } 101 } 102 103 private void exch(int i, int j) { 104 Key swap = pq[i]; 105 pq[i] = pq[j]; 106 pq[j] = swap; 107 } 108 109 // is pq[1..N] a max heap? 110 private boolean isMaxHeap() { 111 return isMaxHeap(1); 112 } 113 114 // is subtree of pq[1..n] rooted at k a max heap? 115 private boolean isMaxHeap(int k) { 116 if (k > n) return true; 117 int left = 2*k; 118 int right = 2*k + 1; 119 if (left <= n && less(k, left)) return false; 120 if (right <= n && less(k, right)) return false; 121 return isMaxHeap(left) && isMaxHeap(right); 122 } 123 124 public Iterator<Key> iterator() { 125 return new HeapIterator(); 126 } 127 128 private class HeapIterator implements Iterator<Key> { 129 130 // create a new pq 131 private MaxPQ<Key> copy; 132 133 // add all items to copy of heap 134 // takes linear time since already in heap order so no keys move 135 public HeapIterator() { 136 if (comparator == null) copy = new MaxPQ<Key>(size()); 137 else copy = new MaxPQ<Key>(size(), comparator); 138 for (int i = 1; i <= n; i++) 139 copy.insert(pq[i]); 140 } 141 142 public boolean hasNext() { return !copy.isEmpty(); } 143 public void remove() { throw new UnsupportedOperationException(); } 144 145 public Key next() { 146 if (!hasNext()) throw new NoSuchElementException(); 147 return copy.delMax(); 148 } 149 } 150 }
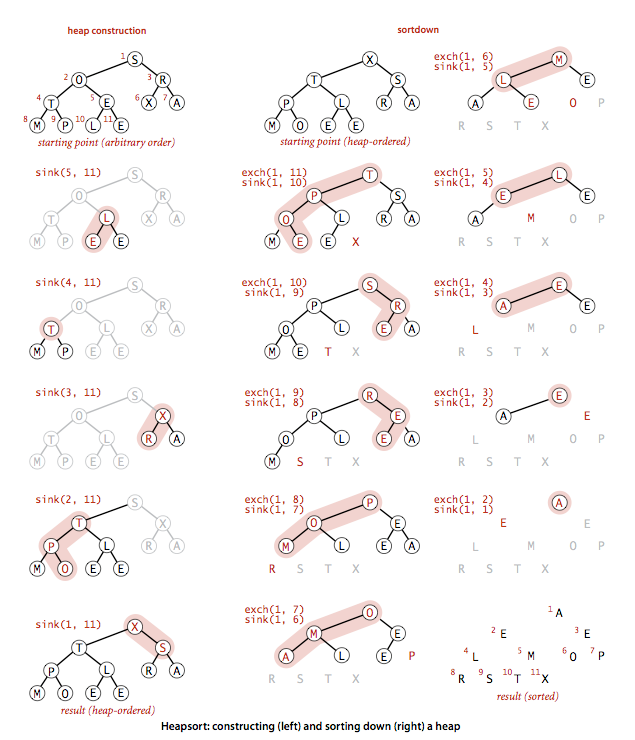
3.堆排序
1 public class Heap 2 { 3 public static void sort(Comparable[] a){ 4 int N = a.length; 5 for (int k = N/2; k >= 1; k--) sink(a, k, N); 6 7 while (N > 1){ 8 exch(a, 1, N); 9 sink(a, 1, --N); 10 } 11 } 12 13 private static void sink(Comparable[] a, int k, int N) 14 { /* as before */ } 15 private static boolean less(Comparable[] a, int i, int j) 16 { /* as before */ } 17 private static void exch(Comparable[] a, int i, int j) 18 { /* as before */ } 19 }
作者: 邹珍珍(Pearl_zhen)
出处: http://www.cnblogs.com/zouzz/
声明:本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出 原文链接 如有问题, 可邮件(zouzhenzhen@seu.edu.cn)咨询.



