动态连通性问题:union-find算法
写在前面的话:
一枚自学Java和算法的工科妹子。
- 算法学习书目:算法(第四版) Robert Sedgewick
- 算法视频教程:Coursera Algorithms Part1&2
本文是根据《算法(第四版)》的个人总结,如有错误,请批评指正。
一、动态连通性问题介绍
1.基本概念:
- 问题的输入是一列整数对,每个整数都表示一个某种类型的对象,一对整数“p q”表示的含义是“p和q相连”。
- “相连”是一种等价关系:1)自反性(p与p相连接);2)对称性(若p连接到q,那么q也连接到p);3)传递性(若p连接到q,q连接到r,则p连接到r)。
- 等价关系将对象分成多个等价类,它们构成多个集合,称为“连通组件”(Connected Components)。
2.目标:设计一个程序,保存所有的整数对信息,并判断一对输入的对象是否相连。
3.应用:
- 计算机网络。若这些数字编号的对象是大型计算机网络中的各计算机设备,点对序列即表示了计算机之间的通信连接。因此我们的算法能够判断对于某两台计算机p和q,要使它们能够互相通信,是需要建立新的连接,还是可以利用已有的线路建立一个通信路径。
- 社交网络。数字编号的物体代表Facebook上的用户,而点对表示朋友关系,那么我们的算法就可以在两个用户之间建立朋友关系,或者查找他们俩有没有“可能认识的人”。
- 变量名的等价性。在某些编程语言中,可以用我们的算法来检测某两个变量是否是等价的(都指向同一对象)。
- 数学上的集合论。可以判断某两个整数是否属于同一集合。
二、动态连通性问题分析和建模
动态连通性问题只要求判断给定的整数p和q是否连通,并不要求给出两者之间的所有连接。设计并查集算法的API封装以下操作:初始化,连接两个对象,查找某对象所在的集合的标识符,判断两对象是否相连,统计连通集合的数目。

图1 并查集算法的API设计
解决连通性问题就是实现并查集算法的API:
- 定义一种数据结构表示已知的连接;
- 基于此数据结构实现高效的union(),find(),connected(),count().
三、union-find算法的实现
下面讨论四种不同的实现,它们均以id[]数组来确定两个对象是否存在于相同的连通分量。
1.quick-find算法
- quick-find算法是保证当且仅当id[p]=id[q]时p和q是连通的,因此同一个连通集合的所有对象的id全部相同。
- find(p):返回p的id,同一个连通集合的所有对象的id全部相同;
- connected(p,q):判断id[p]==id[q]?
- union(p,q):先用 connected(p,q)判断p和q是否相连,若不相连(p所在集合的id为一个值,q所在集合的id为另一个值),遍历数组所有元素,将p所在集合的对象的id全部改为id[q].

图2 quick-find算法:find(5,9)和union(5,9)
1 public class QuickFindUF { 2 private int[] id; // 对象的id 3 private int count; // 连通集合数量 4 5 // 初始化对象id数组 6 public QuickFindUF(int n) { 7 count = n; 8 id = new int[n]; 9 for (int i = 0; i < n; i++) 10 id[i] = i; 11 } 12 13 // 返回连通集合数量 14 public int count() { 15 return count; 16 } 17 18 // 返回对象p的id 19 public int find(int p) { 20 return id[p]; 21 } 22 23 // 判断p和q是否相连 24 public boolean connected(int p, int q) { 25 validate(p); 26 validate(q); 27 return id[p] == id[q]; 28 } 29 30 // 将p和q归并到同一个集合 31 public void union(int p, int q) { 32 validate(p); 33 validate(q); 34 int pID = id[p]; // needed for correctness 35 int qID = id[q]; // to reduce the number of array accesses 36 37 // p q已经在同一个集合则不需要采取任何行动 38 if (pID == qID) return; 39 40 // 将p所在的集合的所有对象重新赋值id为id[q] 41 for (int i = 0; i < id.length; i++) 42 if (id[i] == pID) id[i] = qID; 43 count--; 44 } 45 46 }
quick-find算法分析(含有N个对象):
- 每次find()调用只需访问数组一次;
- 每次归并两个集合的union()操作需要访问数组次数在(N+3)~(2N+1)之间。(最好的情况p所在集合只有p一个对象:2+N+1=N+3,最坏情况除了q以后所有对象都在p所在集合:2+N+N-1=2N+1)
因此使用quick-find算法解决动态连通性问题并且最后使所有对象都在一个连通集合,至少需要调用N-1次union(),即至少(N+3)(N-1)~N2次访问数组。
2.quick-union算法
- quick-find算法的union操作需要遍历整个数组才能完成,为提高union()方法的速度,提出quick-union算法。
- quick-union算法的策略:parent[p]为节点p的父节点,若id[p] == p,则称p为根节点(root),当且仅当两个节点的根节点相等时,两个节点处于同一连通集合中。那么初始状态下的N个节点就可以看成N棵只有一个节点的树构成的“森林”,而id数组则记录了每个节点的父节点,若两个节点的根节点相等,那么这两个节点就是相连接的。
- find(p):沿着路径一直向上回溯,直到找到根节点parent[r] == r;
- union(p,q):先找到节点p和q各自的根节点pRoot和qRoot,然后修改p的父节点parent[p]=qRoot。
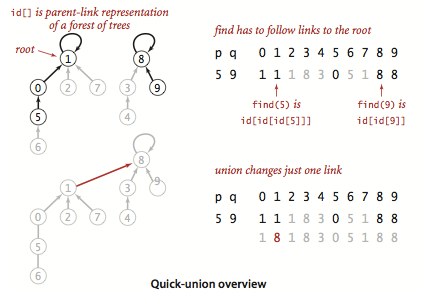
图3 quick-union算法:find(5,9)和union(5,9)
1 public class QuickUnionUF { 2 private int[] parent; // 父节点 3 private int count; // 连通集合数目 4 5 public QuickUnionUF(int n) { 6 parent = new int[n]; 7 count = n; 8 for (int i = 0; i < n; i++) { 9 parent[i] = i; 10 } 11 } 12 13 public int count() { 14 return count; 15 } 16 17 public int find(int p) { 18 while (p != parent[p]) 19 p = parent[p]; 20 return p; 21 } 22 23 public boolean connected(int p, int q) { 24 return find(p) == find(q); 25 } 26 27 public void union(int p, int q) { 28 int rootP = find(p); 29 int rootQ = find(q); 30 if (rootP == rootQ) return; 31 // 将p所在的树连接到q的根节点rootQ上 32 parent[rootP] = rootQ; 33 count--; 34 } 35 36 }
quick-union算法分析(含有N个节点):
- union():所有节点全部归并到一个集合,最坏的情况就是0连接到1,1连接到2,2连接到3...如此循环,构造0-1-2-3-4……-N-1形式的一棵很“高”的树,根节点是N-1,总共访问数组的次数(N-1)+2[1+2+...+(N-1)]+(N-1)~N2
- 前面的(N-1)表示像树上每增加一个节点i(i=1,2,3,...,N-1),find(i)访问数组的总次数;
- 中间的2[1+2+...+(N-1)]表示对树尾部的节点0,find(0)访问数组的总次数;
- 最后的(N-1)表示将节点0的根节点设为i(i=1,2,3,...,N-1),访问数组的总次数.
3.加权quick-union算法
- 加权quick-find算法在quick-find算法修改程序,避免出现高度很高的树。一种加权策略就是记录每棵树的节点个数,并总是在执行union操作时用小树(节点较少)的根节点指向大树(节点较多)来保持平衡。
- 加权quick-find算法策略:增加一个数组sz[]来存储每棵树的节点个数,一开始将sz[]全部初始化为1,每次执行union操作时根据sz[]数组进行判断,将小树根节点指向大树的根节点,并更新大树对应的sz[]值。
 图4 加权quick-find算法降低树高度
图4 加权quick-find算法降低树高度1 public class WeightedQuickUnionUF { 2 private int[] parent; // parent[i] = parent of i 3 private int[] size; // size[i] = number of sites in subtree rooted at i 4 private int count; // number of components 5 6 public WeightedQuickUnionUF(int n) { 7 count = n; 8 parent = new int[n]; 9 size = new int[n]; 10 for (int i = 0; i < n; i++) { 11 parent[i] = i; 12 size[i] = 1; 13 } 14 } 15 16 public int count() { 17 return count; 18 } 19 20 public int find(int p) { 21 while (p != parent[p]) 22 p = parent[p]; 23 return p; 24 } 25 26 public boolean connected(int p, int q) { 27 return find(p) == find(q); 28 } 29 30 public void union(int p, int q) { 31 int rootP = find(p); 32 int rootQ = find(q); 33 if (rootP == rootQ) return; 34 35 // make smaller root point to larger one 36 if (size[rootP] < size[rootQ]) { 37 parent[rootP] = rootQ; 38 size[rootQ] += size[rootP]; 39 } 40 else { 41 parent[rootQ] = rootP; 42 size[rootP] += size[rootQ]; 43 } 44 count--; 45 } 46 }
加权quick-union算法分析(含有N个节点):
- 对于N个节点,加权quick-union算法构造的森林中任意节点的深度最多为lgN(由归纳算法推到得,不明白的朋友可以留言或发邮件询问)
- 因此,在最坏的情况下,find()、connected()和union()的成本增长数量级为lgN。
4.路径压缩的加权quick-union算法
- 理想情况下,希望每个节点都直接连接在它的根节点上,但是又不像quick-find那样union方法要遍历所有节点。要实现路径压缩,只需要为find()添加一个循环,将在路径上遇到的所有点都直接连接到根节点。
- 路径压缩的加权quick-union算法已经是最优的算法了,但是并非所有的操作都能在常数时间内完成。
1 public class PathCompressWQU { 2 private int[] parent; // parent[i] = parent of i 3 private int[] size; // size[i] = number of sites in subtree rooted at i 4 private int count; // number of components 5 6 public PathCompressWQU(int n) { 7 count = n; 8 parent = new int[n]; 9 size = new int[n]; 10 for (int i = 0; i < n; i++) { 11 parent[i] = i; 12 size[i] = 1; 13 } 14 } 15 16 public int count() { 17 return count; 18 } 19 20 public int find(int p) { 21 int temp=p; 22 while (p != parent[p]) 23 p = parent[p]; 24 25 while(temp != parent[p]){ 26 int tempParent = parent[temp]; 27 parent[temp] = parent[p]; 28 temp = tempId; 29 } 30 31 return parent[p]; 32 } 33 34 public boolean connected(int p, int q) { 35 return find(p) == find(q); 36 } 37 38 public void union(int p, int q) { 39 int rootP = find(p); 40 int rootQ = find(q); 41 if (rootP == rootQ) return; 42 43 // make smaller root point to larger one 44 if (size[rootP] < size[rootQ]) { 45 parent[rootP] = rootQ; 46 size[rootQ] += size[rootP]; 47 } 48 else { 49 parent[rootQ] = rootP; 50 size[rootP] += size[rootQ]; 51 } 52 count--; 53 } 54 }
四、四种union-find算法的性能对比

作者: 邹珍珍(Pearl_zhen)
出处: http://www.cnblogs.com/zouzz/
声明:本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出 原文链接 如有问题, 可邮件(zouzhenzhen@seu.edu.cn)咨询.





