数据结构---栈和队
1.栈
1.1栈的定义
栈是只能在表的一端进行插入和删除操作的线性表,其中允许掺入与删除的一端称为栈顶(top),另一端则称为栈底(bottom)。对于栈(a1,a2,...an),元素a1为栈底元素,an为栈顶元素。n=0时为空栈。进栈与出栈分别称为压入和弹出操作。栈的特点是先进后出。
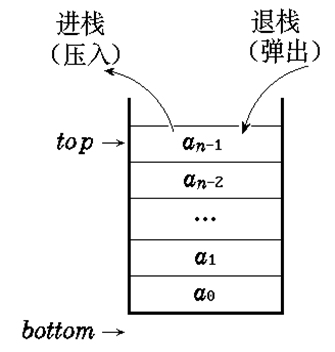
1.2顺序栈
顺序栈可以使用向量作为栈的存储结构,用一维数组s[1:m]表示,用变量top表示栈顶位置,称为栈顶指示器,当top=0时表示张空,top=m时表示栈满。
进栈操作:
判断栈是否满,不满则top++,元素输入s[top]中。(对于栈满top==m时,元素进栈导师上溢)
1 2 3 4 5 6 7 8 9 10 | int PushS(int s[],int m,int top,int x){ if (top==m) stack_overflow();//栈满 top++; s[top]=x;//指示器加1,入栈 return(top); //成功,返top } |
出栈操作:
判断栈是否为空,非空top减1即可。
1 2 3 4 5 6 7 8 9 | int PopS(int s[],int top,int *y){ if (top==0) stack_empty(); //栈空 *y=s[top]; //栈顶元素由y返回 top--; //指示器减1 return(top); //成功,返top } |
性能分析:进栈与出栈操作均不包含循环语句,时间复杂度为O(1),比一般线性表速度快。
1.3链栈
链栈是使用链表作为存储结构的栈,top为其栈顶元素指针,若top==null,不是栈空,一般其存储空间为整个内存,一般不会出现上溢的情况。

链栈的插入:
申请空节点,在顶端插入元素,修改top指针。
1 2 3 4 5 6 7 8 9 10 11 | NODE *PushL(NODE *top,int x){ NODE *s; s=GetListNode(x); //申请结点 if (s){//申请成功,插入 s->next=top; top=s; } return(top); //返回栈顶指针 } |
链栈的删除:
修改栈顶top指针,释放栈顶元素空间。
1 2 3 4 5 6 7 8 9 10 | NODE *PopL(NODE *top){ NODE *s; if (top!=NULL) { s=top; top=top->next; free(s); } return(top);} |
1.4栈的应用
键盘输入;十进制数值转换成二进制数值;表达式求值;过程嵌套与递归调用;回溯求解算法;背包问题等等。
2.队
2.1队的定义
队是限定在表的一端进行插入,队头front,另一端进行删除,队尾rear的线性表。队的特点是先进先出。存储结构有顺序和链式两种。

2.1顺序队
用一维数组Q[1:m]存储队时,m为期最大容量,初始状态rear=front=0,队空,入队时rear加1,出队时front加1,当rear=front时队空,当rear=m时,对满,此时不能进行入队操作,但空间不一定满,出现“假溢出”现象,仅当rear-front=m时才是真满。未必买哪假溢出现象的发生,假想这个队列是首尾相接的循环队列。

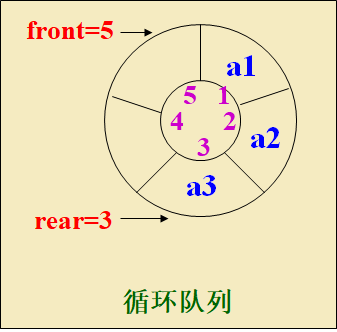
进队插入操作:定位插入位置,判断是否满,不满则插入。rear = (rear + 1) % maxSize;
1 2 3 4 5 6 7 | int rear,int x){ rear=(rear+1)%m;//计算插入位置 if (front==rear)//队满,失败,返回0 return(0); Q[rear]=x; //插入 return(1); //成功,返回1 } |
出队删除操作:判断队是否为空,非空则定位删除位置,进行删除。 front = (front + 1) % maxSize;
1 2 3 4 5 6 7 8 9 | int DelQ(int Q[],int m,int front,int rear,int *y){ if (front==rear)//队空,失败,返回0 return(0); front=(front+1)%m;//计算删除位置 *y=Q[front]; //删除并送入y中 return(1); //成功,返回1 } |
其中:
1)循环队列中判断队空和队满的条件:队空:front==rear 队满:(rear+1)%m==front
2)在循环队列中永远会空一个位置,这是为了判别队空和队满而造成的。
2.3链队
链队是使用链表作为队的存储结构,适用于队的容量无法估计的情况下。使用头指针front指向头结点,尾指针rear指向队尾元素。当rear=front时,队空。
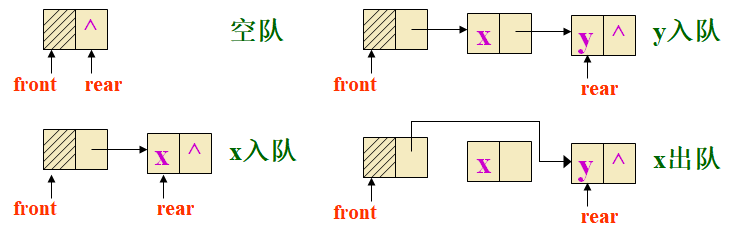
插入操作:
申请结点,插入操作,修改尾指针。
1 2 3 4 5 6 7 8 9 10 11 | NODE *AddLink(NODE *front,NODE *rear, int x){ NODE *s=GetListNode(x); //申请结点 if (s){ rear->next=s;//插入 rear=s;//修改尾指针 return(rear);//成功,返回尾指针 } return(NULL); //失败,返回NULL} |
删除操作:
判断非空,修改头指针指向,删除元素,回收空间。如果此时队空,返回头指针。
1 2 3 4 5 6 7 8 9 10 11 12 13 | NODE *DelLink(NODE *front,NODE *rear, int *y){ NODE *s; if (front==rear) return(NULL);//队空 s=front->next; //取得队头结点 *y=s->data; //保存数据 front->next=s->next; //删除s free(s); //释放s if (front->next==NULL) //队已空 rear=front; return(rear); //返回尾指针 } |
2.4队的应用
多道程序中的CPU管理、缓冲区的设计、二项展开式


【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步