粒子群算法(主要针对连续型函数优化问题)
文章主要参考了以下博文:
1. 简介#
粒子群算法是一种解决最优化问题的通用方法,其优点是求解速度快,数值相对稳定,算法简单。粒子群算法分为连续型粒子群算法和离散型粒子群算法,分别用于解决连续型问题和离散型问题。
粒子群优化算法源自对鸟群捕食行为的研究:一群鸟在区域中随机搜索食物,搜索的策略就是搜寻目前离食物最近的鸟的周围区域。粒子群算法利用这种模型得到启示并应用于解决优化问题:
-
鸟类的飞行空间: 搜索空间,也可以理解为约束
-
鸟(粒子): 可行解
-
鸟类寻找到的食物源: 最优解
在粒子群算法中,每个优化问题的潜在解都是搜索空间中的一只鸟,称之为粒子(在连续性例子群算法中,每一个粒子就代表一个可行解)。所有的粒子都有一个由被优化的函数决定的适应度值,每个粒子还有一个速度决定它们飞翔的方向和距离。然后,粒子们就追随当前的最优粒子在解空间中搜索。
粒子群算法首先在给定的解空间中随机初始化粒子群,待优化问题的变量数决定了解空间的维数(这里表示每个粒子的维度,后面我们会用D表示维度)。每个粒子有了初始位置与初始速度(x表示当前位置,v表示速度,粒子群算法最重要的是对速度公式的更新,因为速度决定了更新的方向,进而决定解的值),然后通过迭代寻优。在每一次迭代中,每个粒子通过跟踪两个“极值”来更新自己在解空间中的空间位置与飞行速度:一个极值就是单个粒子本身在迭代过程中找到的最优解粒子,这个粒子叫作个体极值;(这里的意思是,每个粒子具有记忆性,每个粒子子记得两个值,一个是全部的粒子距离目标的最优值,另一个值是这个粒子曾经历史的最优值) 另一个极值是种群所有粒子在迭代过程中所找到的最优解粒子,这个粒子是全局极值。
2. 连续型粒子群优化算法#
2.1 基本原理#
假设在一个
第
第
整个粒子群迄今为止搜索到的最优位置为全局极值(我的理解是
在找到这两个最优值时,粒子根据如下的式(5)和式(6)分别来更新自己的速度和位置:
式(5)和式(6)是整个粒子群算法最核心的部分,对于式(5),其中:
-
-
-
-
-
式(5)右边由三部分组成:
-
第一部分为“惯性”或“动量”部分,反映了粒子的运动“习惯”,代表粒子有维持自己先前速度的趋势(就是原有的速度);
-
第二部分为“认知”部分,反映了粒子对自身历史经验的记忆或回忆,代表粒子有向自身历史最佳位置逼近的趋势;
-
第三部分为“社会”部分,反映了粒子间协同合作与知识共享的群体历史经验,代表粒子有向群体或邻域历史最佳位置逼近的趋势(对于
-
上面的是基本粒子群算法,下面的标准粒子群算法的更新是这样的,就是在速度
权重更新公式如下(这是其中一种,还有其他的更新方式):
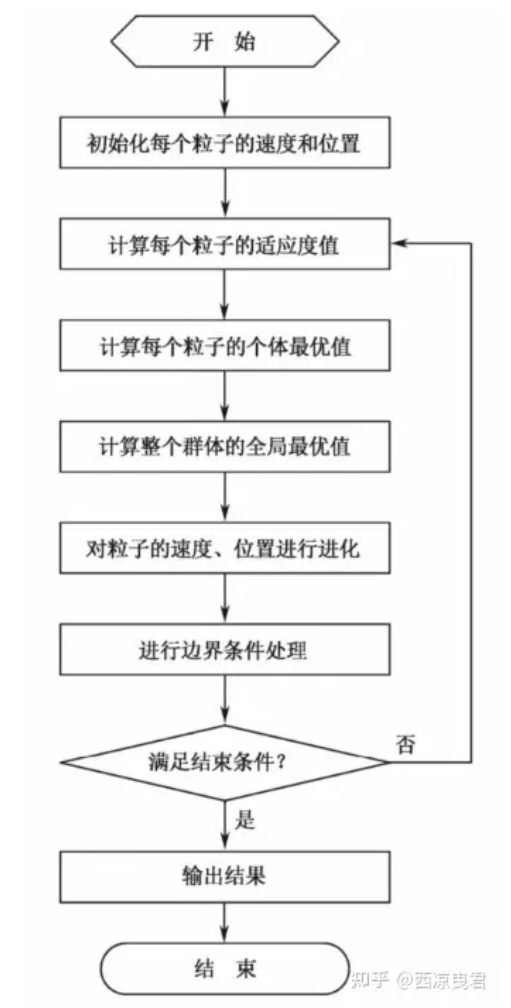
2.2 算法流程#
(1)初始化粒子群,包括群体规模
(2)计算每个粒子的适应度值
(3)对每个粒子,用它的适应度值
(4)对每个粒子,用它的适应度值
(5)迭代更新粒子的速度
(6)进行边界条件处理。
(7)判断算法终止条件是否满足:若是,则结束算法并输出优化结果;否则返回步骤(2)。
2.3 算法详解#
求函数
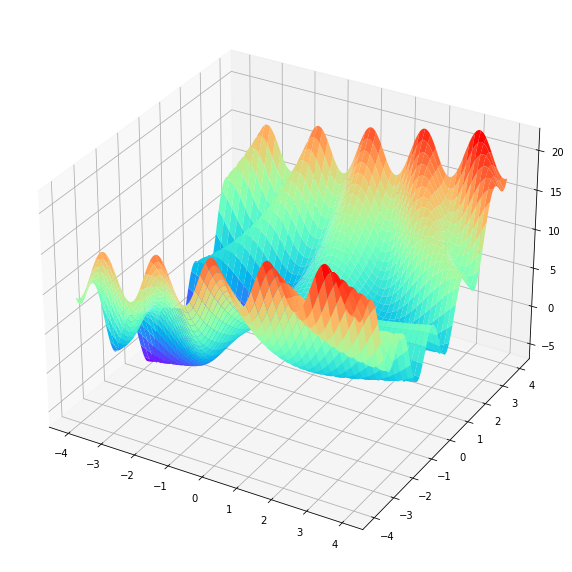
2.3.1 绘图#
首先我们来看看
# 求函数f(x,y) = 3*cos(x * y) + x + y**2的最小值,其中-4 <= x <= 4, -4 <= y <= 4
# 首先绘制这个函数的三维图像
import numpy as np
import matplotlib.pyplot as plt
X = np.arange(-4 ,4 ,0.01)
Y = np.arange(-4 ,4 ,0.01)
x, y = np.meshgrid(X ,Y)
Z = 3*np.cos(x * y) + x + y**2
# 作图
fig = plt.figure(figsize=(10,15))
ax3 = plt.axes(projection = "3d")
ax3.plot_surface(x,y,Z ,cmap = "rainbow")
# ax3.contour(x ,y ,Z ,zdim = "z" ,offset=-2 ,cmap = "rainbow")
plt.show()
2.3.2 连续型粒子群算法求解#
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
# 设置字体和设置负号
matplotlib.rc("font", family="KaiTi")
matplotlib.rcParams["axes.unicode_minus"] = False
# 初始化种群,群体规模,每个粒子的速度和规模
N = 100 # 种群数目
D = 2 # 维度
T = 200 # 最大迭代次数
c1 = c2 = 1.5 # 个体学习因子与群体学习因子
w_max = 0.8 # 权重系数最大值
w_min = 0.4 # 权重系数最小值
x_max = 4 # 每个维度最大取值范围,如果每个维度不一样,那么可以写一个数组,下面代码依次需要改变
x_min = -4 # 同上
v_max = 1 # 每个维度粒子的最大速度
v_min = -1 # 每个维度粒子的最小速度
# 定义适应度函数
def func(x):
return 3 * np.cos(x[0] * x[1]) + x[0] + x[1] ** 2
# 初始化种群个体
x = np.random.rand(N, D) * (x_max - x_min) + x_min # 初始化每个粒子的位置
v = np.random.rand(N, D) * (v_max - v_min) + v_min # 初始化每个粒子的速度
# 初始化个体最优位置和最优值
p = x # 用来存储每一个粒子的历史最优位置
p_best = np.ones((N, 1)) # 每行存储的是最优值
for i in range(N): # 初始化每个粒子的最优值,此时就是把位置带进去,把适应度值计算出来
p_best[i] = func(x[i, :])
# 初始化全局最优位置和全局最优值
g_best = 100 #设置真的全局最优值
gb = np.ones(T) # 用于记录每一次迭代的全局最优值
x_best = np.ones(D) # 用于存储最优粒子的取值
# 按照公式依次迭代直到满足精度或者迭代次数
for i in range(T):
for j in range(N):
# 个更新个体最优值和全局最优值
if p_best[j] > func(x[j,:]):
p_best[j] = func(x[j,:])
p[j,:] = x[j,:].copy()
# p_best[j] = func(x[j,:]) if func(x[j,:]) < p_best[j] else p_best[j]
# 更新全局最优值
if g_best > p_best[j]:
g_best = p_best[j]
x_best = x[j,:].copy() # 一定要加copy,否则后面x[j,:]更新也会将x_best更新
# 计算动态惯性权重
w = w_max - (w_max - w_min) * i / T
# 更新位置和速度
v[j, :] = w * v[j, :] + c1 * np.random.rand(1) * (p[j, :] - x[j, :]) + c2 * np.random.rand(1) * (x_best - x[j, :])
x[j, :] = x[j, :] + v[j, :]
# 边界条件处理
for ii in range(D):
if (v[j, ii] > v_max) or (v[j, ii] < v_min):
v[j, ii] = v_min + np.random.rand(1) * (v_max - v_min)
if (x[j, ii] > x_max) or (x[j, ii] < x_min):
x[j, ii] = x_min + np.random.rand(1) * (x_max - x_min)
# 记录历代全局最优值
gb[i] = g_best
print("最优值为", gb[T - 1],"最优位置为",x_best)
plt.plot(range(T),gb)
plt.xlabel("迭代次数")
plt.ylabel("适应度值")
plt.title("适应度进化曲线")
plt.show()
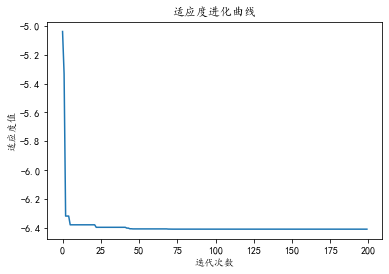


 内含针对连续型问题的粒子群算法原理及python求解代码和适应度函数曲线绘图
内含针对连续型问题的粒子群算法原理及python求解代码和适应度函数曲线绘图


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· AI技术革命,工作效率10个最佳AI工具