基于TRE文章的非线性模型化线性方法

之前写过一篇有关TRE优化模型详解的博文：

https://www.cnblogs.com/zoubilin/p/17270435.html

这篇文章里面的附录给出了非线性模型化线性的方式，具体内容如下：

• 首先是篇文章的变量和原模型（具体见我上面那篇笔记）：
  
  
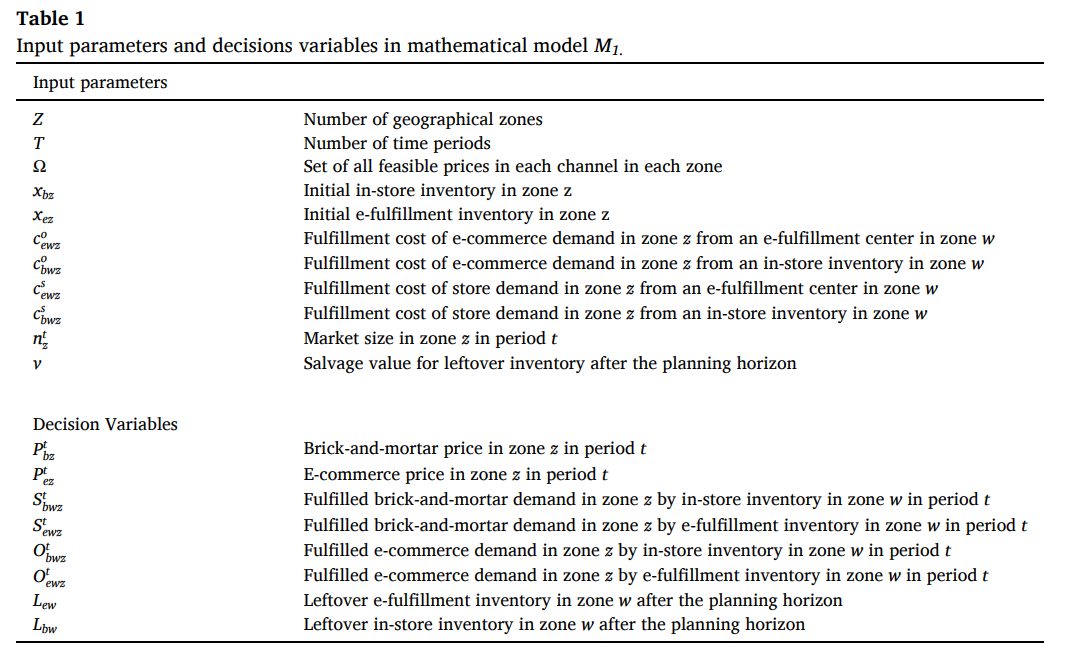
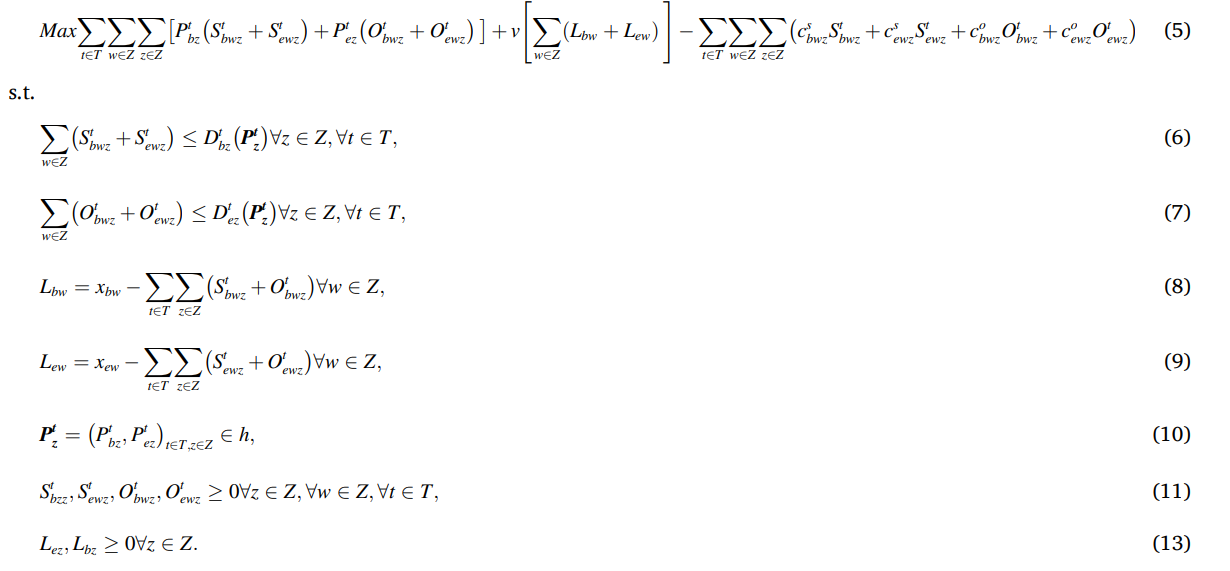
• 其次这篇文章附录给出的非线性化线性的方法：
  
  
  我觉得很经典，所以这几天我废了九牛二虎之力推导了这个附录的公式，并复现了它的化线性的过程•́‸ก

一、目标函数

• 目标函数中的非线性项为：

\[Max\quad{\sum_{t\in{T}}}\sum_{z\in{Z}}[P^t_{bz}\sum_{w\in{Z}}(S^t_{bwz}+S^t_{ewz})+P^t_{ez}\sum_{w\in{Z}}(O^t_{bwz}+O^t_{ewz})] \]

• 引入决策变量：

\[Y^t_{bzi}=\begin{cases} 1,\quad\quad{if\,在t时期z区域渠道b对应的是第i个价格}\\0,\quad\quad{else}\end{cases} \]

\[Y^t_{ezi}=\begin{cases} 1,\quad\quad{if\,在t时期z区域渠道e对应的是第i个价格}\\0,\quad\quad{else}\end{cases} \]

• 此时应加入下面约束条件，即式(A.13)~式(A.14) 和式(A.28)~式(A.29)：

  \[\sum_{i\in{I_{bzi}^t}}Y^t_{bzi}=1 \]
  \[\sum_{i\in{I_{ezi}^t}}Y^t_{ezi}=1 \]
  \[Y^t_{bzi},Y^t_{ezi}\in{\{0,1\}} \]

• 引入价格集合（已知量），其中\(I^t_{bz}、I^t_{ez}\)为对应渠道的可选择价格数量，\(i={1,2,...,I^t_{bz}}或i={1,2,...,I^t_{ez}}\)：

\[\Omega^t_{bz}=\{P^t_{bzi}\}_{i\in{I^t_{bz}}} \]

\[\Omega^t_{ez}=\{P^t_{ezi}\}_{i\in{I^t_{ez}}} \]

• 那么有：\(P^t_{bz}=\sum_{i\in{I^t_{bz}}}P^t_{bzi}Y^t_{bzi}\)、\(P^t_{ez}=\sum_{i\in{I^t_{ez}}}P^t_{ezi}Y^t_{ezi}\)

• 此时，目标函数变为：

\[Max\quad{\sum_{t\in{T}}}\sum_{z\in{Z}}[\sum_{i\in{I^t_{bz}}}P^t_{bzi}Y^t_{bzi}\sum_{w\in{Z}}(S^t_{bwz}+S^t_{ewz})+\sum_{i\in{I^t_{ez}}}P^t_{ezi}Y^t_{ezi}\sum_{w\in{Z}}(O^t_{bwz}+O^t_{ewz})] \]

• 目标函数中仍存在非线性项\(Y^t_{bzi}\sum_{w\in{Z}}(S^t_{bwz}+S^t_{ewz})\)和\(Y^t_{ezi}\sum_{w\in{Z}}(O^t_{bwz}+O^t_{ewz})\)

  所以需要再引入下面决策变量，也就是式(A.6)~式(A.7)：

  \[V^t_{bzi}=Y^t_{bzi}\sum_{w\in{Z}}(S^t_{bwz}+S^t_{ewz}) \]
  \[V^t_{ezi}=Y^t_{ezi}\sum_{w\in{Z}}(O^t_{bwz}+O^t_{ewz}) \]

  此时目标函数变为下式，也就是式(A.8) 的由来：

\[ Max\quad{\sum_{t\in{T}}}\sum_{z\in{Z}}[(\sum_{i\in{I^t_{bz}}}P^t_{bzi}V^t_{bzi})+(\sum_{i\in{I^t_{ez}}}P^t_{ezi}V^t_{ezi})] \]

设\(\sum_{w\in{Z}}(S^t_{bwz}+S^t_{ewz})\)的上限为\(a\)，\(\sum_{w\in{Z}}(O^t_{bwz}+O^t_{ewz})\)的上限为\(b\)，要彻底转换目标函数变为线性，需要增加新的约束如下，包含了式(A.15)-式(A.18)、式(A.33)-式(A.34)：

\[V^t_{bzi}\leq{a}Y^t_{bzi} \]

\[V^t_{ezi}\leq{b}Y^t_{ezi} \]

\[V^t_{bzi}\leq{\sum_{w\in{Z}}(S^t_{bwz}+S^t_{ewz})} \]

\[V^t_{ezi}\leq{\sum_{w\in{Z}}(O^t_{bwz}+O^t_{ewz})} \]

\[V^t_{bzi}\geq[{\sum_{w\in{Z}}(S^t_{bwz}+S^t_{ewz})}]-a(1-Y^t_{bzi}) \]

\[V^t_{ezi}\geq[{\sum_{w\in{Z}}(O^t_{bwz}+O^t_{ewz})}]-b(1-Y^t_{ezi}) \]

\[V^t_{bzi},V^t_{ezi}\geq{0} \]

\[\sum_{i\in{I^t_{bzi}}}V^t_{bzi}={\sum_{w\in{Z}}(S^t_{bwz}+S^t_{ewz})} \]

\[\sum_{i\in{I^t_{ezi}}}V^t_{ezi}=\sum_{w\in{Z}}(O^t_{bwz}+O^t_{ewz}) \]

二、约束条件

• 非线性项为\(D^t_{bz}(P^t_{z})\)和\(D^t_{ez}(P^t_{z})\)

• 经过上面的转换，有：

  • \(e^{\beta_{0z}+\beta_{1z}P^t_{bz}}=e^{\beta_{0z}+\beta_{1z}\sum_{i\in{I^t_{bz}}}(P^t_{bzi}Y^t_{bzi})}\)其中，\(Y^t_{bzi}\)是一个0-1变量，所以又可以写成：\(e^{\beta_{0z}+\beta_{1z}P^t_{bz}}=\sum_{i\in{I^t_{bz}}}Y^t_{bzi}e^{\beta_{0z}+\beta_{1z}P^t_{bzi}}\).

  • 同理，\(e^{\beta_{0z}+\beta_{1z}P^t_{ez}}=\sum_{i\in{I^t_{ez}}}Y^t_{ezi}e^{\beta_{0z}+\beta_{1z}P^t_{ezi}}\)

• 令

  \[r^t_{bzi}=e^{\beta_{0z}+\beta_{1z}P^t_{bzi}} \]
  \[r^t_{ezi}=e^{\beta_{0z}+\beta_{1z}P^t_{ezi}} \]

  即式(A.1)~式(A.2)，那么有：

  \[D^t_{bz}(P^t_z)=n^t_z×\frac{\sum_{i\in{I^t_{bz}}}Y^t_{bzi}r^t_{bzi}}{\sum_{i\in{I^t_{bz}}}Y^t_{bzi}r^t_{bzi}+\sum_{i\in{I^t_{ez}}}Y^t_{ezi}r^t_{ezi}+1} \]
  \[D^t_{ez}(P^t_z)=n^t_z×\frac{\sum_{i\in{I^t_{ez}}}Y^t_{ezi}r^t_{ezi}}{\sum_{i\in{I^t_{bz}}}Y^t_{bzi}r^t_{bzi}+\sum_{i\in{I^t_{ez}}}Y^t_{ezi}r^t_{ezi}+1} \]

• 为了将\(D^t_{bz}(P^t_{z})\)和\(D^t_{ez}(P^t_{z})\)化为线性，令：

  \[R^t_z=\frac{1}{\sum_{i\in{I^t_{bz}}}Y^t_{bzi}r^t_{bzi}+\sum_{i\in{I^t_{ez}}}Y^t_{ezi}r^t_{ezi}+1} \]

  即式(A.3)。那么\(D^t_{bz}(P^t_{z})=n^t_zR^t_z\sum_{i\in{I^t_{bz}}}Y^t_{bzi}r^t_{bzi}\)，\(D^t_{ez}(P^t_{z})=n^t_zR^t_z\sum_{i\in{I^t_{ez}}}Y^t_{ezi}r^t_{ezi}\)，需要明确的是：\(\sum_{i\in{I^t_{bz}}}Y^t_{bzi}r^t_{bzi}+\sum_{i\in{I^t_{ez}}}Y^t_{ezi}r^t_{ezi}\geq{0}\)，故\(R^t_z\leq{1}\)

• 此时仍存在非线性项\(\sum_{i\in{I^t_{bz}}}R^t_zY^t_{bzi}r^t_{bzi}\)和\(\sum_{i\in{I^t_{ez}}}R^t_zY^t_{ezi}r^t_{ezi}\)

  令：

  \[U^t_{bzi}=R^t_zY^t_{bzi} \]
  \[U^t_{ezi}=R^t_zY^t_{ezi} \]

  即式(A.4)-式(A.5)。此时需要新增的约束条件如下，包含了式(A.21)-式(A.27)、式(A.32)-式(A.34)：

  \[U^t_{bzi},U^t_{ezi}\geq{0} \]
  \[R^t_z\geq{0} \]
  \[U^t_{bzi}\leq{Y^t_{bzi}} \]
  \[U^t_{ezi}\leq{Y^t_{ezi}} \]
  \[U^t_{bzi}\leq{R^t_z} \]
  \[U^t_{ezi}\leq{R^t_z} \]
  \[U^t_{bzi}\leq{R^t_z}-(1-Y^t_{bzi}) \]
  \[U^t_{ezi}\leq{R^t_z}-(1-Y^t_{ezi}) \]
  \[\sum_{i\in{I^t_{bzi}}}U^t_{bzi}=R^t_z \]
  \[\sum_{i\in{I^t_{ezi}}}U^t_{ezi}=R^t_z \]

\[R^t_z+\sum_{i\in{I^t_{bz}}}U^t_{bzi}r^t_{bzi}+\sum_{i\in{I^t_{ez}}}U^t_{ezi}r^t_{ezi}=1 \]

• 此时约束条件(6)、(7)变为：

\[\sum_{w\in{Z}}(S^t_{bwz}+S^t_{ewz})\leq{n^t_z\sum_{i\in{I^t_{bz}}}U^t_{bzi}r^t_{bzi}} \]

\[\sum_{w\in{Z}}(O^t_{bwz}+O^t_{ewz})\leq{n^t_z\sum_{i\in{I^t_{ez}}}U^t_{ezi}r^t_{ezi}} \]

• 那么\(a=n^t_z\sum_{i\in{I^t_{bz}}}U^t_{bzi}r^t_{bzi}\)，\(b=n^t_z\sum_{i\in{I^t_{ez}}}U^t_{ezi}r^t_{ezi}\)。约束\(V^t_{bzi}\leq{a}Y^t_{bzi}\)和\(V^t_{ezi}\leq{b}Y^t_{ezi}\)分别变为：

  \[V^t_{bzi}\leq{(n^t_z\sum_{i\in{I^t_{bz}}}U^t_{bzi}r^t_{bzi}})Y^t_{bzi}=n^t_zU^t_{bzi}\sum_{i\in{I^t_{bz}}}r^t_{bzi}Y^t_{bzi} \]
  \[V^t_{ezi}\leq{(n^t_z\sum_{i\in{I^t_{ez}}}U^t_{ezi}r^t_{ezi})}Y^t_{ezi}=n^t_zU^t_{ezi}\sum_{i\in{I^t_{ez}}}r^t_{ezi}Y^t_{ezi} \]

  • 已知\(V^t_{bzi}\geq{0}\)，当\(Y^t_{bzi}=0\)时，上面的第一条约束条件变为\(V^t_{bzi}\leq{0}\)，此时\(V^t_{bzi}\)应为0；当\(Y^t_{ezi}=1\)时，上面的约束条件变为\(V^t_{bzi}\leq{n^t_zU^t_{bzi}r^t_{bzi}}\)，此时\(V^t_{bzi}\)的取值应当为\(0\leq{V^t_{bzi}}\leq{n^t_zU^t_{bzi}r^t_{bzi}}\)。

    综上和同理，在约束\(V^t_{bzi},V^t_{ezi}\geq{0}\)下，式(A.19) 和式(A.20) 被推导出：

  \[V^t_{bzi}\leq{a}Y^t_{bzi}\quad{}→\quad{}V^t_{bzi}\leq{n^t_zU^t_{bzi}r^t_{bzi}} \]
  \[V^t_{ezi}\leq{b}Y^t_{ezi}\quad{}→\quad{}V^t_{bzi}\leq{n^t_zU^t_{bzi}r^t_{bzi}} \]

  • 对于约束条件\(V^t_{bzi}\geq[{\sum_{w\in{Z}}(S^t_{bwz}+S^t_{ewz})}]-a(1-Y^t_{bzi})\)和\(V^t_{ezi}\geq[{\sum_{w\in{Z}}(O^t_{bwz}+O^t_{ewz})}]-b(1-Y^t_{ezi})\)，它们分别变为：

    \[V^t_{bzi}\geq[{\sum_{w\in{Z}}(S^t_{bwz}+S^t_{ewz})}]-(n^t_z\sum_{i\in{I^t_{bz}}}U^t_{bzi}r^t_{bzi})(1-Y^t_{bzi}) \]
    \[V^t_{ezi}\geq[{\sum_{w\in{Z}}(O^t_{bwz}+O^t_{ewz})}]-(n^t_z\sum_{i\in{I^t_{ez}}}U^t_{ezi}r^t_{ezi})(1-Y^t_{ezi}) \]

    当\(Y^t_{bzi}=0\)时，上面第一条约束条件变为\(\sum_{w\in{Z}}(S^t_{bwz}+S^t_{ewz})\leq{n^t_z\sum_{i\in{I^t_{bz}}}U^t_{bzi}r^t_{bzi}}\)这与文中式（6）相同；当\(Y^t_{bzi}=1\)时，它则变为\(V^t_{bzi}=\sum_{w\in{Z}}(S^t_{bwz}+S^t_{ewz})\)，而这又被约束条件\(\sum_{i\in{I^t_{bzi}}}V^t_{bzi}={\sum_{w\in{Z}}(S^t_{bwz}+S^t_{ewz})}\)包含。

    综上及同理，约束条件\(V^t_{bzi}\geq[{\sum_{w\in{Z}}(S^t_{bwz}+S^t_{ewz})}]-a(1-Y^t_{bzi})\)和\(V^t_{ezi}\geq[{\sum_{w\in{Z}}(O^t_{bwz}+O^t_{ewz})}]-b(1-Y^t_{ezi})\)均属于重复约束，可被消除。

由此，所有公式已全部被推出，但还多了两条约束：

• 对于约束条件\(U^t_{bzi}\leq{R^t_z}-(1-Y^t_{bzi})\)有：

  • \(Y^t_{bzi}=0\)时，\(R^t_z\geq{0}\)，该约束已存在；\(Y^t_z=1\)时，\(U^t_{bzi}=R^t_{z}\)，该约束已被\(\sum_{i\in{I^t_{bzi}}}U^t_{bzi}=R^t_z\)所包含。

  • 综上及同理，约束条件\(U^t_{bzi}\leq{R^t_z}-(1-Y^t_{bzi})\)和\(U^t_{ezi}\leq{R^t_z}-(1-Y^t_{ezi})\)属于重复约束，均可被删除。

以上就是这篇论文公式全部的推导，上面是所使用的非线性化线性的方法简例如下。

三、简例

(1) 带有0-1变量的非线性规划问题

\[z=x_1x_2 \]

其中决策变量\(x_1\in{\{0,1\}}\),\(0\leq{x_2}\leq{a}\)

那么我们可以用下面的方法化为线性规划：

• 首先设一个新的决策变量\(y=x_1x_2\)，并将问题转化为：

  \[y\leq{ax_1} \]
  \[y\leq{x_2} \]
  \[y\geq{x_2-a(1-x_1)} \]
  \[y\geq{0} \]

• 由此，问题变为了线性问题

(2) 带分母变量的非线性规划问题

\[min\quad\frac{x+2y+3}{4x+5y} \]

\(s.t.\)

\[6x+7y\leq{8} \]

\[9x+10y\geq{0} \]

\[x,y\geq{0} \]

• 令\(z=\frac{1}{4x+5y}\)，此时目标函数变为：\((x+2y)z+3z\)，但仍含有非线性项，此时我们又令：\(xz=u,yz=v\)，那么可以得到：

  \[min\quad{u+2v+3z} \]

  \(s.t.\)

  \[6u+7v\leq{8z} \]
  \[9u+10v\geq{0} \]
  \[u,v,z\geq{0} \]

• 解上面的线性规划问题，可得到\(u,v,z\)的精确解，之后可代入式子解方程，得到\(x,y\)的精确解。