Cplex求解教程（基于OPL语言，可作为大规模运算输入参考）

最近导导让牛牛改篇论文，牛牛在她的指导下把非线性问题化成了线性。然鹅，化成线性后的模型决策变量和约束条件均达到上百甚至上千个，这让牛牛犯了难，以下方法或许能为这样大规模模型的变量和约束输入提供思路(๑•́₃ •̀๑)

一、问题描述及模型建立

• 指派问题： 分配\(n\)人去做\(n\)项工作；每人做且只做一项工作；若分配第\(i\)人去做第\(j\)项工作，需花费\(c_{ij}\)成本。问应如何分配工作使总成本最小？

• 模型建立：

\[min\quad\sum^n_{i=1}\sum^n_{j=1}c_{ij}x_{ij} \]

\(s.t.\)

\[\sum^n_{j=1}x_{ij}=1,\forall{i=1,2,\dots,n} \]

\[\sum^n_{i=1}x_{ij}=1,\forall{j=1,2,\dots,n} \]

二、模型参数变量及对应OPL语法

• 参数（已知量）：\(n\)、\(c_{ij}\)，均为整型；

  • OPL定义参数(int/float)：int n=5或者n=...，如果为连续型变量，int改为float即可定义小数；

  • n=...允许n先不定义它是多少，用三个点表示。这种写法实现的是模型文件和数据文件分开写。

• 集合（已知量）：\([1..n]\)；

  • OPL定义集合(range)：语法为range 变量名=1..n

  • 上面问题可以写成range worker=1..n；1..n中的两个点也是CPLEX语法，指从1到n，注意一定是两个点。

  • 定义好了集合，模型中再遇到i∈1..n时，就可以简写成i in worker了；也可以直观写成i in 1..n，看个人编程喜好。

• 变量：\(x_{ij}\)，为0-1布尔型；

  • OPL定义变量(dvar)：语法为dvar 数据类型 变量

  • 上面问题可定义为dvar boolean x[Worker][Job]或dvar bool x[1..n][1..n]

  • 此外，数据类型除了boolean，还有整型(int)，正整数(int+)、连续型(float)等。如定义一个正整数x则为: dvar int+ x

• 定义模型时的符号有

  • 最小化问题(minmize)

    • OPL语法：minimize

  • 约束(subject to)

    • OPL语法：subject to

• 定义约束时的符号有：

  • 求和号\(\sum\)，OPL中可表示为sum

  • 任意号\(\forall\)，OPL中可表示为forall，如\(\forall{i}\in{1,..n}\)可表示为forall(i in 1..n)

CPLEX编程思想： 先定义已知量（参数、集合），再定义未知量（决策变量），然后采用"集合语言"写目标和约束。

三、Cplex求解（OPL语言）

基于上面的模型进行求解：

• 首先编写已知量\(n，c_{ij}、1..n\)：

int n=...; // 参数n
range Worker=1..n; // 工人集合
range Job=1..n; // 任务集合
int c[Worker][Job]=...; // 成本参数

• 编写决策变量\(x_{ij}\)

dvar boolean x[Worker][Job];  // 决策变量

• 编写目标函数

minimize sum(i in Worker)sum(j in Job) c[i][j]*x[i][j];

• 编写约束条件

subject to
{ forall(i in 1..n)
    sum(j in 1..n) x[i][j] == 1;//约束1
  forall(j in 1..n) 
    sum(i in 1..n) x[i][j] == 1;//约束2
}

• 写入Cplex中.mod文件如下：
  

再将参数\(n,c_{ij}\)数据写入.dat文件：

n=3; // 3个工人去完成3个任务
c=[[3,8,2],[8,4,6],[6,2,10]]; // 成本矩阵

最后将这两个文件放入同一个运行配置中进行求解。本文分别将上面两个文件命名为demo1.mod和demo1_data.dat，运行配置命名为confit_demo(运行配置必须为英文名，不能为中文)

得出的求解结果如下：

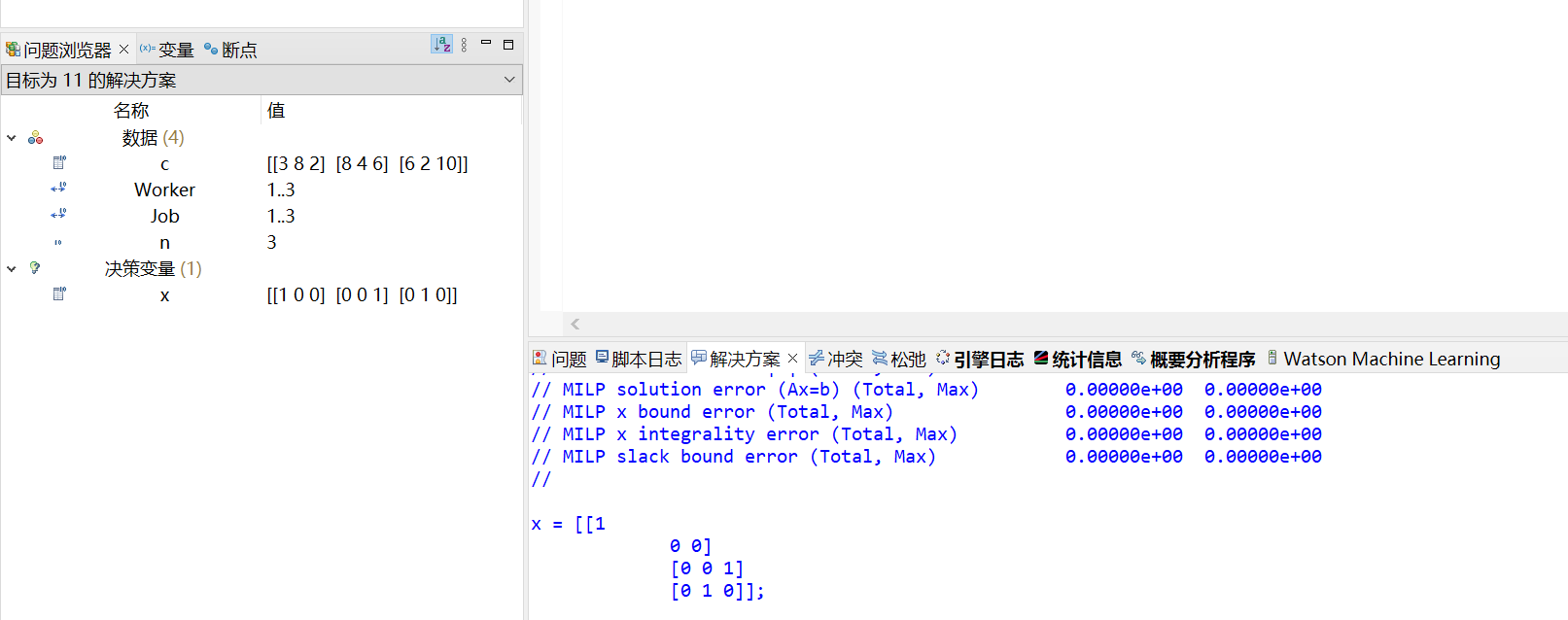
即\(x_{11},x_{23},x_{32}=1\)，其余决策变量为\(0\)