深度学习（七）——神经网络的卷积操作

卷积操作

一、torch.nn中Convolution Layers函数的介绍

1. 参数介绍

• nn.Conv1d: Conv取自Convolution的前四个字母，1d代表的是一个一维操作。

• nn.Conv2d: 2d表示是一个二维的操作，比如图像就是一个二维的。

• 其余参数不常用，见官网文档：torch.nn — PyTorch 2.0 documentation

2. torch.nn和torch.nn.functional的区别

• torch.nn是对torch.nn.functional的一个封装，让使用torch.nn.functional里面的包的时候更加方便

• torch.nn包含了torch.nn.functional，打个比方，torch.nn.functional相当于开车的时候齿轮的运转，torch.nn相当于把车里的齿轮都封装好了，为我们提供一个方向盘

• 如果只是简单应用，会torch.nn就好了。但要细致了解卷积操作，需要深入了解torch.nn.functional

• 打开torch.nn.functional的官方文档，可以看到许多跟卷积相关的操作：torch.nn.functional — PyTorch 2.0 documentation

二、torch.nn.functional.conv2d 介绍

官网文档：torch.nn.functional.conv2d — PyTorch 2.0 documentation

torch.nn.functional.conv2d(input, weight, bias=None, stride=1, padding=0, dilation=1, groups=1)

1. 参数详解

• input: 输入，数据类型为tensor，形状尺寸规定为：(minibatch, 几个通道(in_channels), 高, 宽)

• weight: 权重。更专业地来说可以叫卷积核，形状尺寸规定为：(输出的通道(out_channel), \(in\_channel\over{groups}\)(groups一般取1), 高, 宽 )

• bias: 偏置。

• strids: 步幅。

• padding: 填充。

2. 举例讲解参数strids

（1）理论

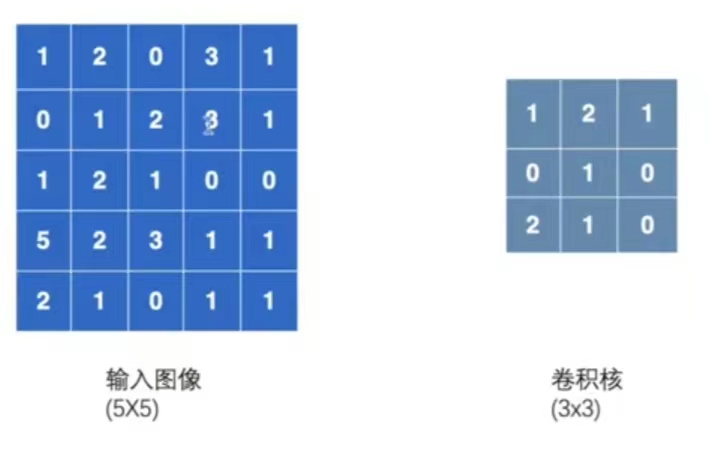
输入一个5×5的图像，其中的数字代表在每个像素中的颜色显示。卷积核设置为3×3的大小。

• strids参数的输入格式是单个数或者形式为 (sH,sW) 的元组，可以理解成：比如输入单个数：strids=1，每次卷积核在图像中向上下或左右移1位；如果输入strids=(2,3)，那么每次卷积核在图像中左右移动（横向移动）时，是移动2位，在图像中上下移动（纵向移动）时，是移动3位。

• 本例设置strids=1

第一次移位：

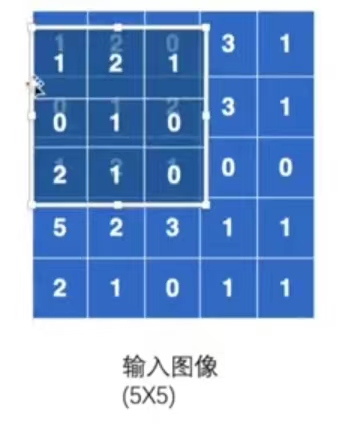
• 基于上述的假设，在做卷积的过程中，需要将卷积核将图像的前三行和前三列进行匹配：
  

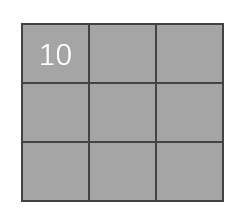
• 在匹配过后，进行卷积计算：对应位相乘然后相加，即

  \[1×1+2×2+0×1+0×0+1×1+2×0+1×2+2×1+1×0=10 \]

• 上面的得出的\(10\)可以赋值给矩阵，然后作为一个输出
  

• 之后卷积核可以在图像中进行一个移位，可以向旁边走1位或2位，如下图（向右走2位）。具体走多少位由strids参数决定，比如strids=2，那就是走2位。本例设置stride=1。
  

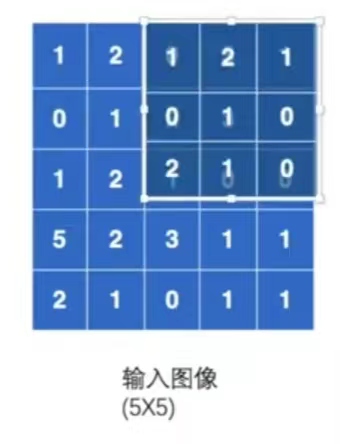
第二次移位：

• 向右移动一位，进行卷积计算：

  \[2×1+0×2+3×1+1×0+2×1+3×0+2×2+1×1+0×0=12 \]

• \(12\)可以赋值给矩阵，然后作为一个输出
  

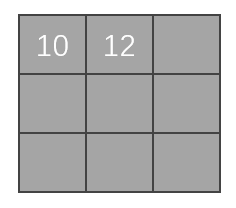
第三次移位：

• 向右移动一位，进行卷积计算：

  \[0×1+3×2+1×1+2×0+3×1+1×0+1×2+0×1+0×0=12 \]

• \(12\)可以赋值给矩阵，然后作为一个输出
  

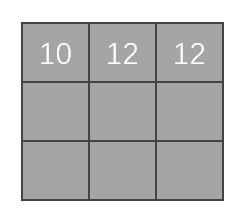
• 第三次移位后，发现卷积核已经没办法向右移位，进行匹配了。所以我们在纵向上，向下走：
  

第四次移位：

• 在最开始的位置上，向下移动一位，进行卷积计算：

  \[0×1+1×2+2×1+1×0+2×1+1×0+5×2+2×1+2×0=18 \]

• \(18\)可以赋值给矩阵，然后作为一个输出
  

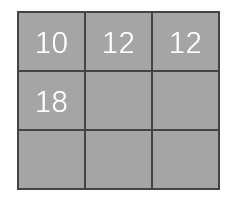
第五次移位：

• 在上面的基础上，向右移一位，进行卷积计算：

  \[1×1+2×2+3×1+2×0+1×1+0×0+2×2+3×1+1×0=16 \]

• \(16\)可以赋值给矩阵，然后作为一个输出
  

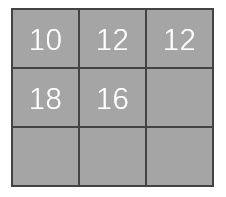
以此类推，走完整个图像，最后输出的矩阵如下图。这个矩阵是卷积后的输出。

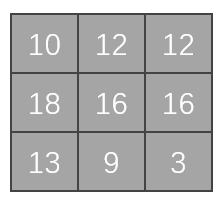
（2）程序操作

将上面的过程写到程序内：

import torch
import torch.nn.functional as F

# 构造输入图像（input参数输入的数据类型为tensor,并且为2维）
input=torch.tensor([[1,2,0,3,1],
                    [0,1,2,3,1],
                    [1,2,1,0,0],
                    [5,2,3,1,1],
                    [2,1,0,1,1]])

# 构造卷积核（数据类型也是tensor，并且为2维）
kernel=torch.tensor([[1,2,1],
                     [0,1,0],
                     [2,1,0]])

#查看尺寸,输出后发现并不符合参数输入的尺寸标准，所以需要进一步转换数据
print(input.shape) #[Run]  torch.Size([5, 5])
print(kernel.shape) #[Run]  torch.Size([3, 3])

#转换input、kernel数据
input=torch.reshape(input,(1,1,5,5))  #torch.reshape(tensor数据,想变成的格式尺寸(batch=1,通道=1,5×5))
kernel=torch.reshape(kernel,(1,1,3,3))

#查看尺寸,输出后发现符合参数输入的尺寸标准
print(input.shape) #[Run]  torch.Size([1, 1, 5, 5])
print(kernel.shape) #[Run]  torch.Size([1, 1, 3, 3])

# 进行卷积操作
#stride=1,输出结果与上面矩阵一致
output=F.conv2d(input,kernel,stride=1)
print(output)
"""
[Run]
tensor([[[[10, 12, 12],
          [18, 16, 16],
          [13,  9,  3]]]])
"""

#stride=2
output2=F.conv2d(input,kernel,stride=2)
print(output2)
"""
[Run]
tensor([[[[10, 12],
          [13,  3]]]])
"""

3. 举例讲解参数padding

padding的作用是在输入图像的左右两边进行填充，padding的值决定填充的大小有多大，它的输入形式为一个整数或者一个元组 ( padH, padW )，其中，padH=高，padW=宽。默认padding=0，即不进行填充。

（1）理论

• 仍输入上述的5×5的图像，并设置padding=1，那么输入图像将会变成下图，即图像的上下左右都会拓展一个像素，然后这些空的地方像素（里面填充的数据）都默认为0。
  

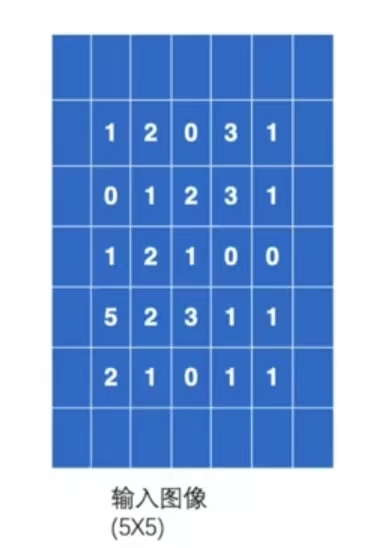
• 按上面的顺序进行卷积计算，第一次移位时在左上角3×3的位置，卷积计算公式变为：

  \[0×1+0×2+0×1+0×0+1×1+2×0+0×2+0×1+1×0=1 \]

• 以此类推，完成后面的卷积计算，并输出矩阵

（2）程序操作

在上面的代码后，加入这串代码，以验证padding的操作：

output3=F.conv2d(input,kernel,stride=1,padding=1)
print(output3)
"""
[Run]
tensor([[[[ 1,  3,  4, 10,  8],
          [ 5, 10, 12, 12,  6],
          [ 7, 18, 16, 16,  8],
          [11, 13,  9,  3,  4],
          [14, 13,  9,  7,  4]]]])
"""