人工智能领域的一般概念、思想和定义

算法

数据类型

数据通常可由两个部分组成：

（1）特征数据：或称输入数据，是输入到算法中的数据。

（2）标签数据：或称输出数据，是需要学习的算法输出。

学习类型

（1）监督学习(SL)：从包含特征值（输入值）和标签值（输出值）的样本数据集中进行学习。

（2）无监督学习(UL)：从仅包含特征值（输入值）的样本数据集中进行学习。

（3）强化学习(RL)：通过从反复实验中不断试错来学习，并根据收到的奖励和惩罚来更新最佳行动策略。

任务类型

（1）估计：也被称为似然或回归，是指标签数据是（连续的）实数值的情况，在计算机中通常表示为浮点数。

（2）分类：是指标签数据由有限数量的分组或者类别组成的情况，这些类别通常由离散值（正自然数）表示，在计算机中表示为整数。

方法类型

人工智能、机器学习（ML）、深度学习（DL）。其中，深度学习中的“深度”在这里表示神经网络具有多个隐藏层，深度学习是机器学习的子集，因此也是人工智能的子集。

神经网络

主要通过与OLS回归比较，展示神经网络的不同之处。先定义数学函数y=2x²-(1/3)x³，再使用线性回归方式进行估计（或函数逼近），然后再应用神经网络进行估计。下面，先绘制并观察函数图像（输入值与输出值之间的关系图）：

import numpy as np
import pandas as pd
from pylab import plt,mpl
plt.style.use('seaborn')

def f(x):
    return 2*x**2-1/3*x**3
x = np.linspace(-2,4,25)   #输入值
print(x)
y=f(x)   #调用函数，输出值
print(y)

plt.figure(figsize=(10,6))
plt.plot(x,y,'ro')

"""
numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None, axis=0)
参数含义：
start:返回样本数据开始点
stop:返回样本数据结束点
num:生成的样本数据量，默认为50
endpoint：True则包含stop；False则不包含stop
retstep：If True, return (samples, step), where step is the spacing between samples.(即如果为True则结果会给出数据间隔)
dtype：输出数组类型
axis：0(默认)或-1

plt.figure(figsize=(a,b))
参数含义：a、b分别表示figure 的大小为宽、长（单位为inch）
"""

输出图像：

 

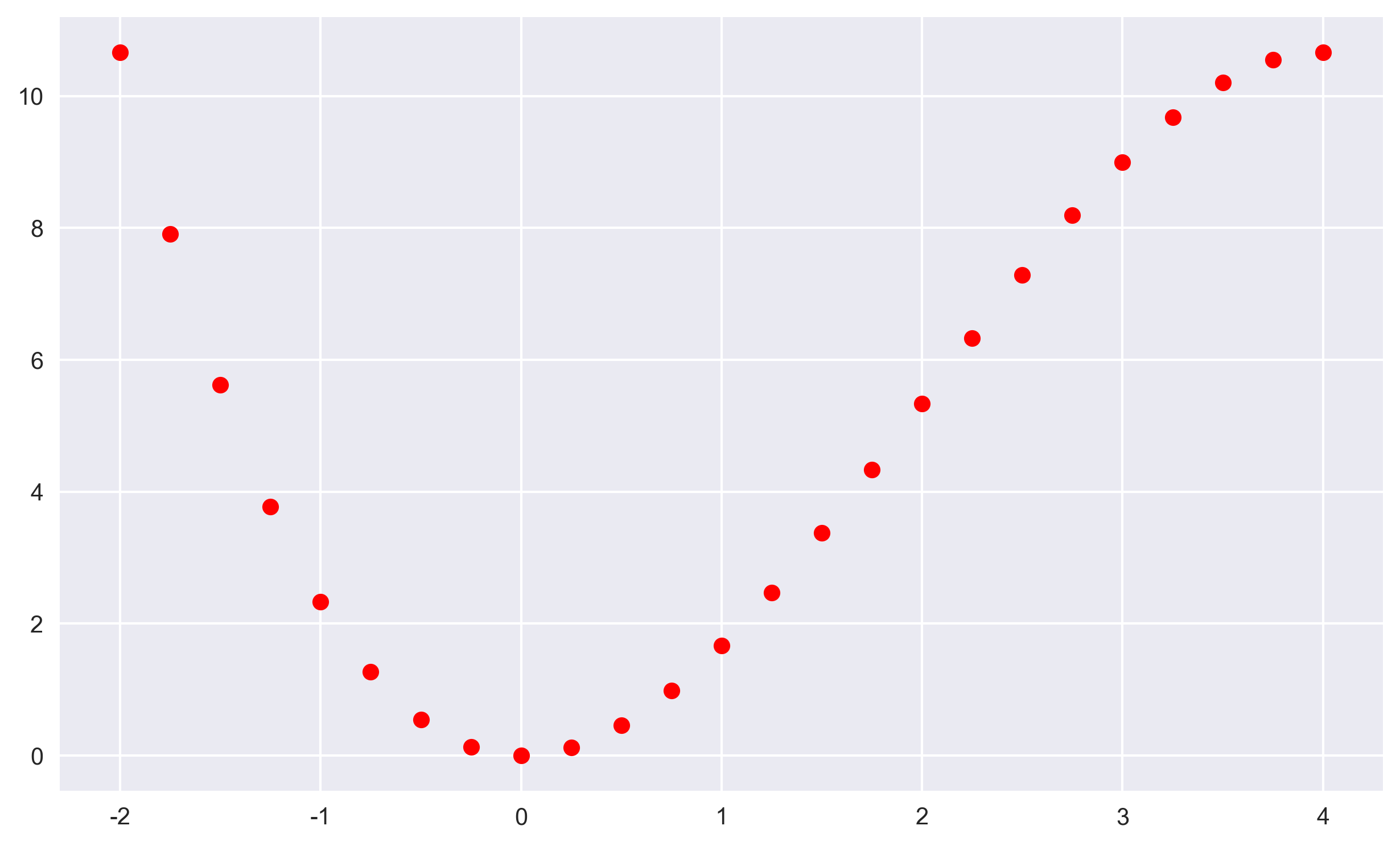
 OLS回归

在统计回归中，上述给定的输入值x和输出值y也称为样本（数据）。统计回归通常将问题定义为找到一个函数，尽可能逼近输入值（也成为自变量）和输出值（也称为因变量）之间的函数关系。

 以一个简单的OLS线性回归为例，假设输入值和输出值之间具有线性关系，需要求解的问题是以下线性方程式找到最优参数 α 和 β

 

 

 对于给定输入值x₁,...,x_n和输出值y₁,...,y_n，最优解将使得输出值与近似输出值之间的MSE最小：

 

 对于简单的线性回归，可以通过公式计算出最优参数(α^*, β^*)的解析解，如以下公式所示：

 

 

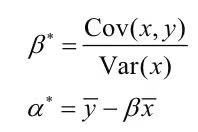
使用以上线性回归的理论，通过Python代码逼近输出值以判断最优参数：

beta = np.cov(x,y,ddof=0)[0,1]/np.var(x)   #计算β的最优解
print(beta)
alpha=y.mean()-beta*x.mean()   #计算α的最优解
y_=alpha+beta*x   #计算估计输出值
MSE=((y-y_)**2).mean()   #根据估计输出值计算MSE
print(MSE)
plt.figure(figsize=(10,6))
plt.plot(x,y,'ro',label='sample data')
plt.plot(x,y_,lw=3.0,label='linear regression')
plt.legend()
plt.show()

输出结果：

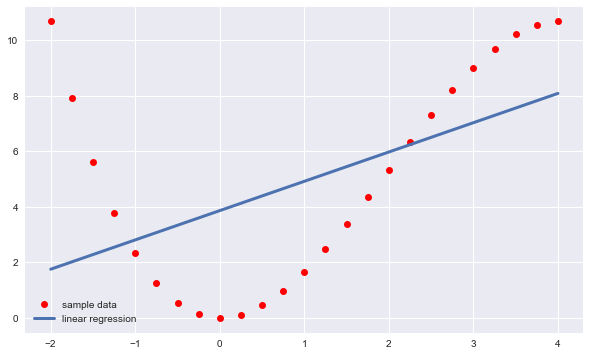
OLS回归并不限于简单的线性关系，除了常数项和一次项，高次项也可作为回归的基函数被加入进来。对于不超过三次项的基函数，都可以使用包含二次项和三次项的OLS回归进行完美逼近并完美恢复关系：

plt.figure(figsize=(10,6))
plt.plot(x,y,'ro',label='sample data')
for deg in [1,2,3]:              
    reg=np.polyfit(x,y,deg=deg)  #回归训练
    y_=np.polyval(reg,x)         #回归预测
    MSE=((y-y_)**2).mean()       #计算MSE
    print(f'deg={deg} | MSE={MSE:.5f}')
    plt.plot(x,np.polyval(reg,x),label=f'deg={deg}')
plt.legend();

输出结果：

 

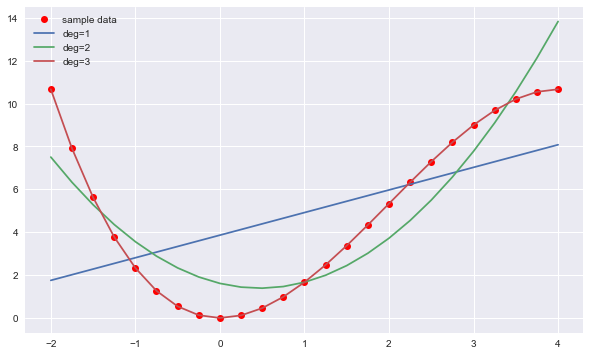
deg=1 | MSE=10.72195

deg=2 | MSE=2.31258

deg=3 | MSE=0.00000

 从上图及输出结果中可以看出，3次项回归线可100%逼近原函数，MSE值为0。可见通过OLS回归可以分别恢复原始函数中二次项和三次项系数的精确值。

神经网络估计

并不是所有关系都是简单的线性关系或高阶线性关系，这时就需要借助神经网络（neural network, NN）等方法进行建模。神经网络可以在不需要知道函数关系情况下近似各种函数关系。

 1. scikit-learn

使用scikit-learn中的MLPRegressor类，该类可用DNN进行回归估计，DNN也称为多层感知器。估计过程如下：

"""
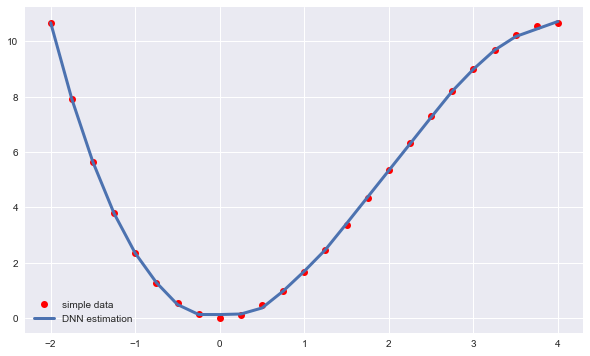
MLPRegressor详解
hidden_layer_sizes：形式为元组，默认为(100,)，数组维度表示隐藏层数量，数字代表隐藏层中神经元的数量。如3*[256]=[256,256,256]，表示有3个隐藏层，每层有256个神经元
learning_rate_init：使用的初始学习率。它控制更新权重时的步长。仅当solver=“gd”或“adam”时使用。
max_iter：默认值为200，最大迭代次数
其他参数请见：https://scikit-learn.org/stable/modules/generated/sklearn.neural_network.MLPRegressor.html?highlight=mlpregressor
"""
from sklearn.neural_network import MLPRegressor
model=MLPRegressor(hidden_layer_sizes=3*[256],
                   learning_rate_init=0.03,
                   max_iter=5000)
model.fit(x.reshape(-1,1),y)   #拟合
y_=model.predict(x.reshape(-1,1))  #预测
MSE=((y-y_)**2).mean()
print(MSE)
plt.figure(figsize=(10,6))
plt.plot(x,y,'ro',label='simple data')
plt.plot(x,y_,lw=3.0,label='DNN estimation')
plt.legend();

输出结果：