统计 - 标准差(SD) vs 标准误差(SE)

标准差: standard deviation, 又叫标准偏差, 是方差的平方根. SAS 对其定义为:

其中, d 是自由度, 默认等于 n-1. 

标准误: Standard Error of Mean. 又叫标准误差. 也写作SEM. 计算公式是:

 Descriptive Statistics :: Base SAS® 9.4 Procedures Guide: Statistical Procedures, Fifth Edition

 

以下内容来源于 Standard Error of Mean(s.e.m.) - minks - 博客园 (cnblogs.com)

· 来源：http://www.dxy.cn/bbs/thread/6492633#6492633

 6楼：

“据我所知，SD( standard deviation )反应的是观测值的变异性，其表示平均数的代表性，而SEM是 standard error of mean, 是平均数的抽样误差，反应平均数的抽样准确性，由于真实值是不知道的，统计估计值的准确性无法度量，但利用统计学方法可以度量精确性。试验的误差来源有系统误差和抽样误差（随机误差），系统误差易于克服，抽样误差由许多无法控制的内因和外因，带有偶然性，在试验中即使十分小心也难以消除，但可以通过增加重复数来来降低。 对于重复数少的小样本（n≤30）用mean ± S.E.M.，重复数多的大样本（n＞30）用 mean ± SD。”

 

· WIKI: https://en.wikipedia.org/wiki/Standard_error

The standard error of the mean (SEM) is the standard deviation of the sample-mean's estimate of a population mean. (It can also be viewed as the standard deviation of the error in the sample mean with respect to the true mean, since the sample mean is an unbiased estimator.) SEM is usually estimated by the sample estimate of the population standard deviation (sample standard deviation) divided by the square root of the sample size (assuming statistical independence of the values in the sample):

where

s is the sample standard deviation (i.e., the sample-based estimate of the standard deviation of the population), and

n is the size (number of observations) of the sample.

 

· 区分“standard deviation”（标准差）和“standard error”（标准误（差））

标准差：衡量一组数的离散程度（一组数据偏离其均值的波动幅度，不论这组数据是总体还是样本）。标准误：样本统计量的标准差，是衡量样本抽样的误差的指标，或者说用样本统计量估计总体参数的精度。统计量本身就是由样本算得的。

另外，标准误其实也是一种理论上存在的东西，一般来说总体无法逐一确定里面的元素，这样也就无法穷尽所有可能的样本，当然也就无法计算出理论上的抽样误差。一般还是根据抽样数据去估计抽样误差。

来源：http://www.zhihu.com/question/21925923

standard deviation 计算公式：

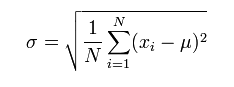
简单来说就是一组数据的每一个数与该组数据的平均值比较，通过得出来的数值看这组数据的离散程度。比如，全班男同学身高都差不多是1.75m，那么我们可以说这个班的男生身高标准差很小，因为大家都接近平均值就是说数据很集中。可是，五个姚明，十个潘长江组成一组，嗯，这个身高数据很离散，参差不齐，标准差很大....

standard error 是样本统计均值的标准差。每次抽取的样本都有一个样本均值和标准差，这些样本的均值重新组成一个样本，这个样本的标准差就是SE。
在现实中，我们无法得知总体情况，总是以样本的分布情况去推断总体。比如，我国在校大学生每月伙食费用是多少。对于这个问题，我们不能全国范围统计各大高校每个同学的伙食费，于是，我们就用样本推断总体大概情况以得出我们所需要的数据。比如，抽取我国都东西南北部分高校部分同学的伙食费进行研究。而此时，标准误产生了。它是衡量样本抽样的误差的指标。

再举一个例子说清楚问题。
比如总体是1 2 3 4 5 6 7 8 9 10 总体平均数是：5.5
而甲对总体进行抽样，可能得到 5 8 3 2 平均数是4.5
乙进行抽样，得到 3 7 9 2 平均数5.25
丙抽样，得到 4 6 9 2 4 1 平均数为4.3
丁...............................平均数为x
那么，4.5， 5.25 ，4.3.........x 组成一个新分布，这是一个以样本平均数为分布的，那么这个分布的标准差是什么呢？利用公式，我们可以得出这个分布的标准差，而这个标准差就是标准误。（当然这个分布的统计量有平均数，标准差，方差，相关系数等等。而我们这里以平均数为栗子。）

如果知道总体的标准差，
如果，不知道总体的标准差，用样本的标准差，采用它的无偏估计
简单说就是统计量（样本）的标准差。

 

· 来源： http://blog.sciencenet.cn/blog-479412-481776.html

统计教材上一般都写标准误表示均数的抽样误差，这对于初学者很难理解。这里通过举例来说明含义。

比如，有一个学校，学校中共有1000名学生，则这1000名学生可以作为这个学校学生的总体。如果我想了解所有学生的身高，采用随机抽样，抽取了50人。这50人就是一个样本。这里需要注意：一个样本并不是指一个人，而是指一次抽样。一个样本可以是1个人，也可以是100人，这里的1和100就是样本大小。

从理论上讲，抽样误差表示这样的意思：即如果不止抽样一次，而是抽样10次，每次都50人，那么我就有10个均数和标准差。总体1000人，一个样本，即50人。每个样本都能计算计算一个均数和标准差。

以这10个均数作为原始数据，仍然能计算出一个均数和标准差，以这10个均数计算出的标准差就称之为标准误。这是理论上的含义，实际的含义就代表抽样误差的大小，即抽取的样本代表性好不好，抽样误差越小，代表性越好，反之，代表性越差。 在实际中，很难对总体进行多次抽样（重复试验），因此有了单次试验（一个样本）就得出SE的方法：SE=SD/sqrt(n). SD越大，SE越大；n是样本大小，n越大，SE越小。

如果我对学校中的1000人都测量了身高，那理论上就没有标准误，也就是没有抽样误差了，因为我测量了总体，这时就不存在标准误了。但是标准差是存在的，因为这1000人的身高肯定不同，肯定会有波动。这里就充分表明了标准差和标准误的区别了。

标准差与标准误的意义、作用和使用范围均不同。标准差(亦称单数标准差）一般用s 表示,是表示个体间变异大小的指标,反映了整个样本对样本平均数的离散程度,是数据精密度的衡量指标;而标准误一般用S_x 表示,反映样本平均数对总体平均数的变异程度,从而反映抽样误差的大小,是量度结果精密度的指标。

样本标准差：

样本平均数的标准误：

 

例子：This shows four samples of increasing size. Note how the standard error reduces with increasing sample size.

 

标准差SD和标准误差SE的区别可以这样表述：标准差是某个样本数据方差的平方根，它衡量的是该样本数据的离散程度；标准误是在多次抽样中样本均值的标准差，衡量的是样本均值的离散程度。而在实际的抽样中，习惯用样本均值来推断总体均值，那么样本均值的离散程度（标准误）越大，抽样误差就越大，应此可以用标准误来衡量抽样误差的大小。
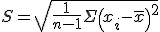
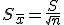
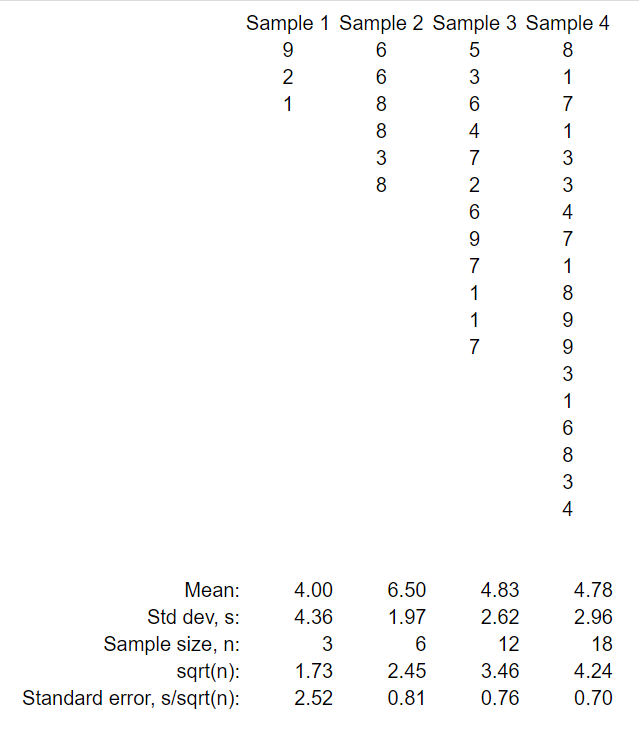
在实际的应用中，标准差主要有两点作用，一是用来对样本进行标准化处理，即样本观察值减去样本均值，然后除以标准差，这样就变成了标准正态分布；二是通过标准差来确定异常值，常用的方法就是样本均值加减n倍的标准差。标准误的作用主要是用来做区间估计，常用的估计区间是均值加减n倍的标准误。

Mean +/- SD 表示样本点距离样本均值的距离，比如已知总体服从均值为mean(用样本估计的), 标准差为SD(用样本估计的)的正态分布，则有68%的数据点落在Mean +/- SD 这个区间，95%的数据点落在 Mean +/- 1.96SD 区间。

Mean +/- SE 表示总体均值的置信区间（样本均值Mean和总体均值的相对距离），比如若总体服从正态分布，则总体均值有68%的概率落在Mean +/- SE区间，有95%概率落在Mean +/- 1.96SE区间。这里Mean和SE是样本均值和样本均值的标准误差。

 

在展示统计数据的时候，样本量n、均值、标准差SD都是要展示的，这样读者可以马上计算出SE和CI。SE和CI主要用来表达样本均值与总体真实均值的相对距离，是显著性的补充。一个很宽的CI很可能不是一个好的估计，即便p值显著，也说明估计不可靠。

 

以下摘自https://bbs.pinggu.org/thread-1189387-1-1.html：

标准差计算的是一组数据偏离其均值的波动幅度，不管这组数是总体数据还是样本数据。你看standard deviation，说的就是“偏离”，只是在翻译为中文时，失去了其英文涵义。

而标准误，衡量的是我们在用样本统计量去推断相应的总体参数（常见如均值、方差等）的时候，一种估计的精度。样本统计量本身就是随机变量，每一次抽样，都可以根据抽出的样本情况计算出一个不同的样本统计量值。理论上来讲，从既定的总体中按照既定的样本规模n，穷尽所有可能抽出的样本（不妨假设为NN），根据这些样本可以计算出NN个样本统计量值，把这些统计量值分组绘成直方图（X轴为分组的统计量数值，Y轴为落在某一分组区间内的频率），则这个直方图就反应了样本统计量的分布情况（即抽样分布）。既然是分布，当然就有均值和方差。如果所有可能的样本统计量值的平均值就是总体均值，这就是无偏估计。如果所有可能的样本统计量值的方差在所有用于估计总体参数的统计量里最小，这就是有效估计。因此，抽样分布的标准差（也就是标准误）越小，则用样本统计量去估计总体参数时，精度就越高。所以，你明白为什么叫标准误（standard error）了。一般意义上讲，standard error反映的是用样本统计量去估计总体参数的时候，可能发生的平均“差错”。

不妨这么理解吧，如果总体平均值是160，抽样误差是5，就是说用抽得的样本平均数去推断总体平均数时，平均差错可能在5左右；如果抽样误差是3，精度当然就比5要高啦。不同的总体、不同的样本规模，这个精度当然是不同的。如果总体的变异本身很小（也就是总体标准差小），样本规模越大，这种情况下精度当然就高啦。另外，根据大数定律，当样本规模大到一定程度的时候，不管总体是什么分布，样本平均数都会近似服从正态分布，这就为计算抽样误差（标准误）提供了理论依据。

最后总结：标准差还是标准误，注意看其英文原意，就可以把握个八九不离十了。本质上二者是同一个东西（都是标准差），但前者反映的是一种偏离程度，后者反映的是一种“差错”，即用样本统计量去估计总体参数的时候，对其“差错”大小（也即估计精度）的衡量。

 

其他参考 : (89条消息) 误差棒到底是个什么棒？到底棒不棒！_和你在一起^_^的博客-CSDN博客_误差棒

http://changingminds.org/explanations/research/statistics/standard_error.htm

https://blog.sciencenet.cn/blog-45423-397760.html

https://blog.csdn.net/soga235/article/details/114546691