数据结构和算法（五）

图

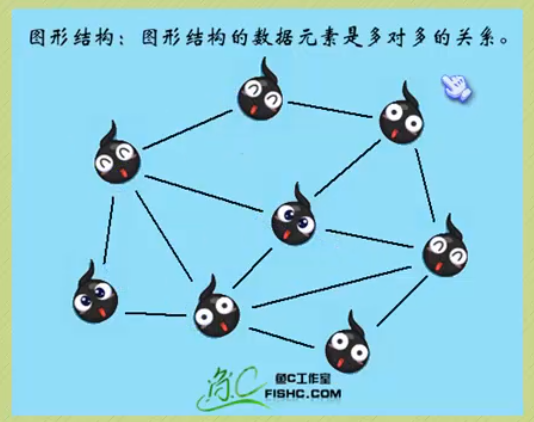
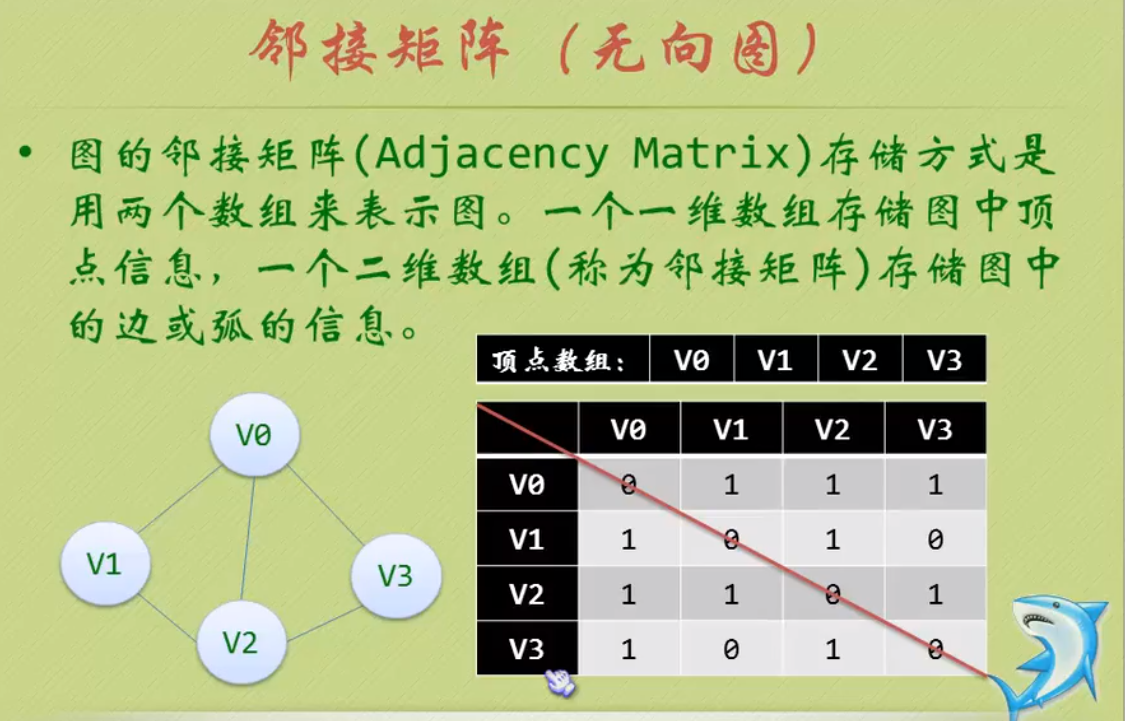
• 定义：图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G(V,E)。其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。

  

• 线性表中把数据元素叫元素，树中叫结点，在图中数据元素则称之为顶点(Vertex)。

• 线性表可以没有数据元素，称为空表，树中可以没有结点，叫做空树，图结构顶点集合V要有穷非空。

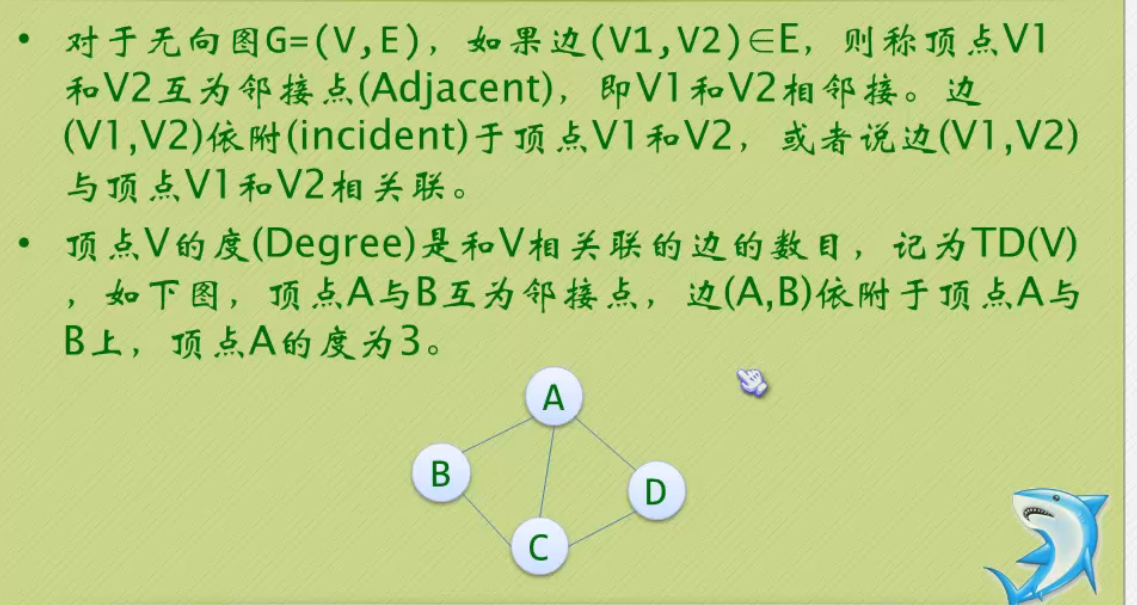
• 线性表中，相邻的数据元素之间具有线性关系；树结构中，相邻两层的结点具有层次关系；图结构中，任意两个顶点之间都可能有关系，顶点之间的逻辑关系用边来表示，边集可以是空的。

• 无向边：若顶点Vi到Vj之间的边没有方向，则称这条边为无向边(Edge)，用无序偶(Vi，Vj)来表示。

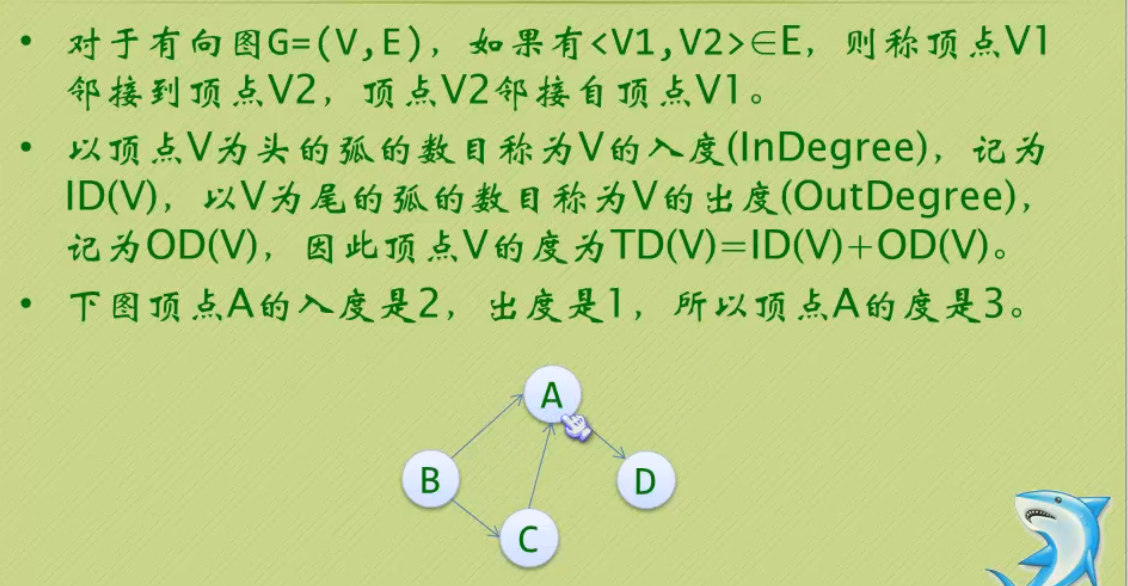
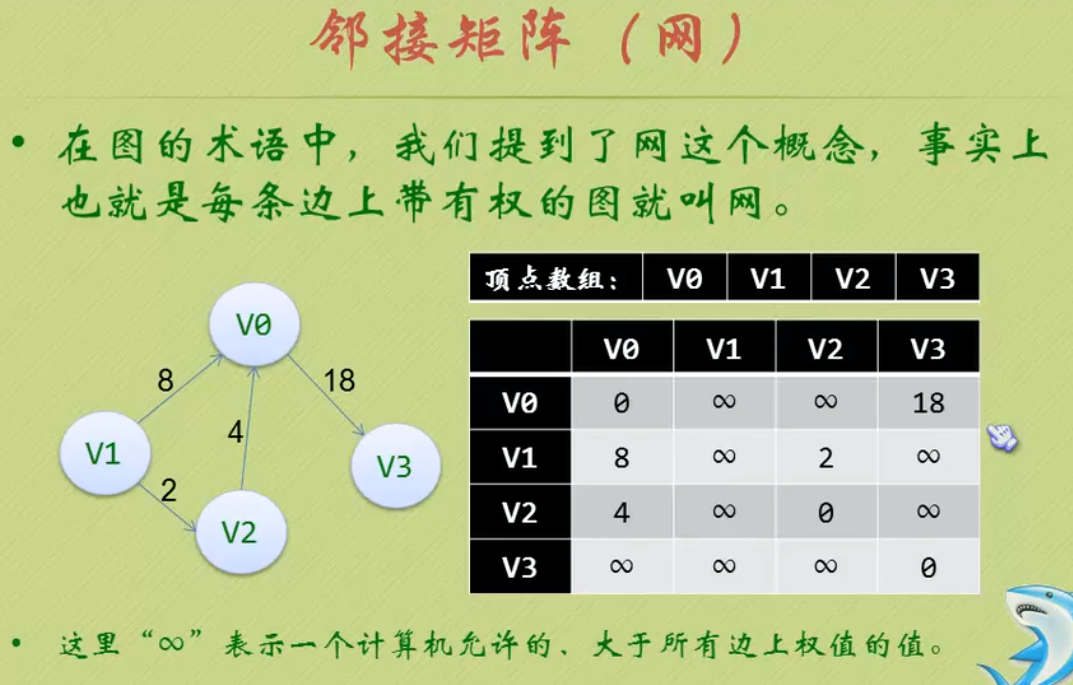
• 有向边：若从顶点Vi到Vj的边有方向，则称这条边为有向边，也成为弧(Arc)，用有序偶<Vi，Vj>来表示，Vi称为弧尾，Vj称为弧头。

• 简单图：在图结构中，若不存在顶点到其自身的边，且同一条边不重复出现，则称这样的图为简单图。

• 无向完全图：在无向图中，如果任意两个顶点之间都存在边，则称该图为无向完全图。含有n个顶点的无向完全图有n(n-1)/2条边。

• 有向完全图：在有向图中，如果任意两个顶点之间都存在方向互为相反的两条弧，则称该图为有向完全图。含有n个顶点的有向完全图有n(n-1)条边。

• 稀疏图和稠密图：通常认为边或弧数小于n*logn(n是顶点的个数)的图称为稀疏图，反之称为稠密图。

• 权(Weight)：与图的边或弧相关的数，带权的图通常称为网(Network)。

• 

图的顶点与边之间的关系

• 

• 

• 

• 

• 

• 

• 

• 

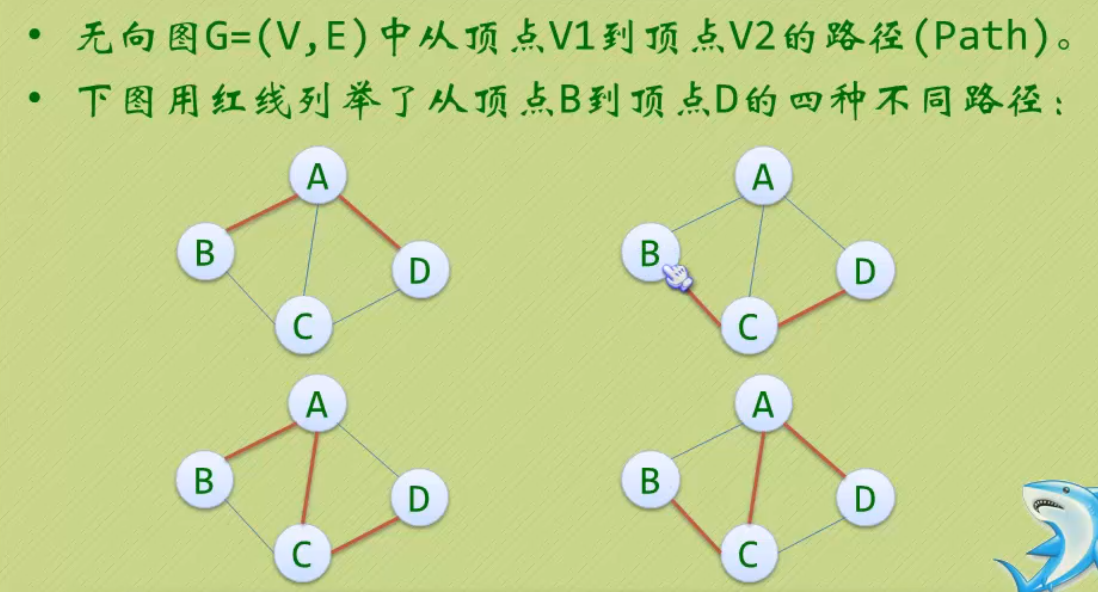
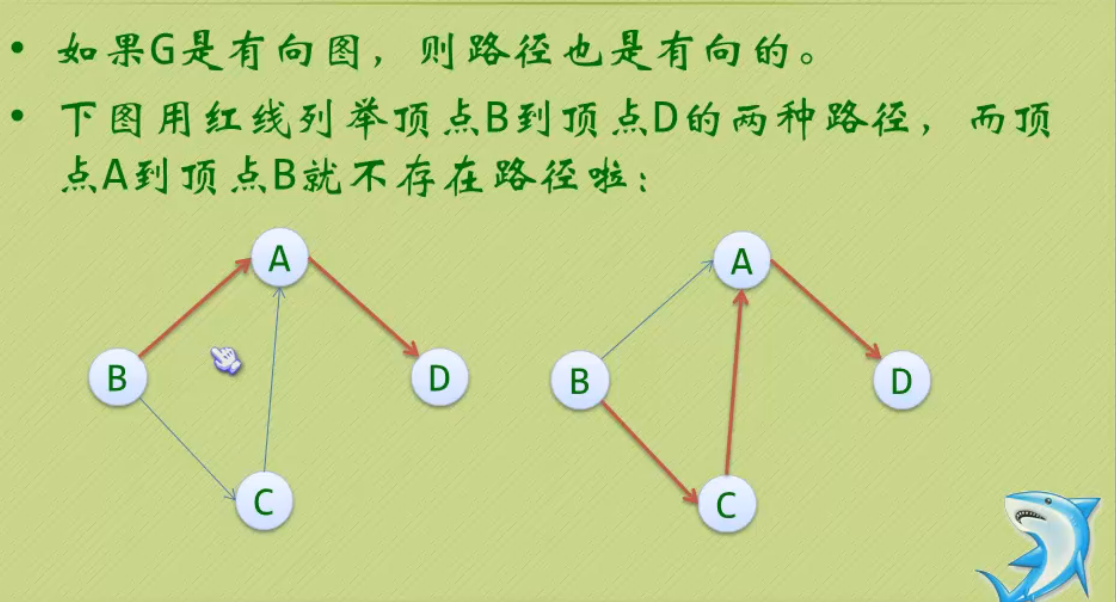
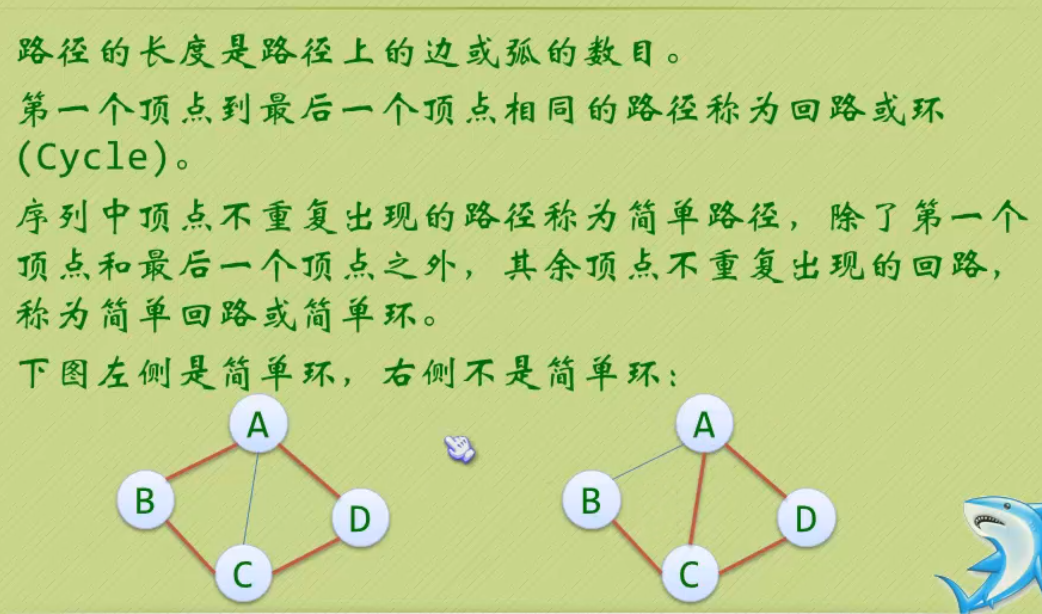
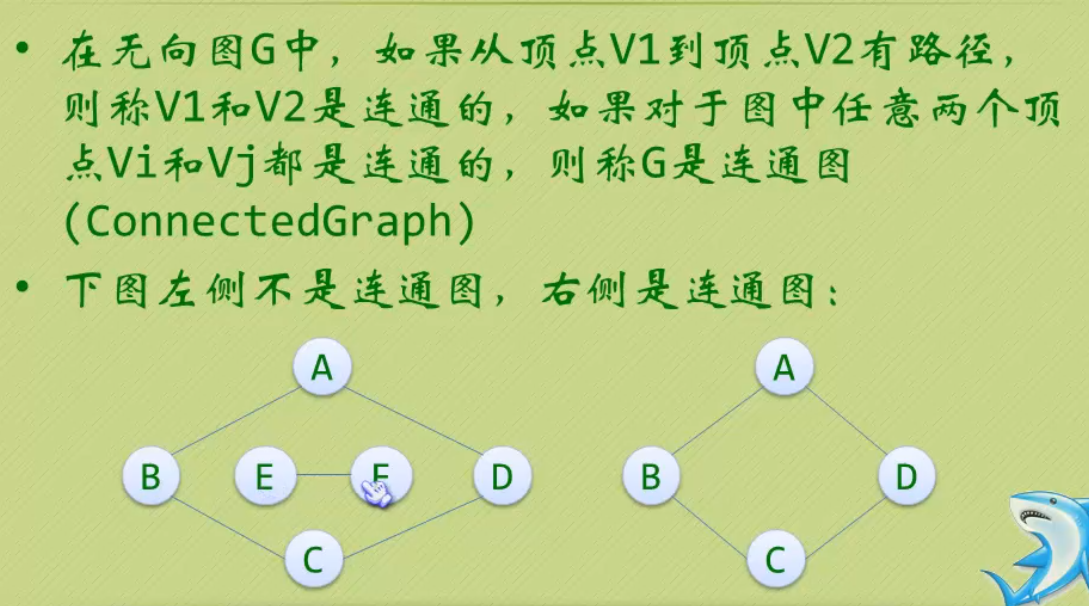
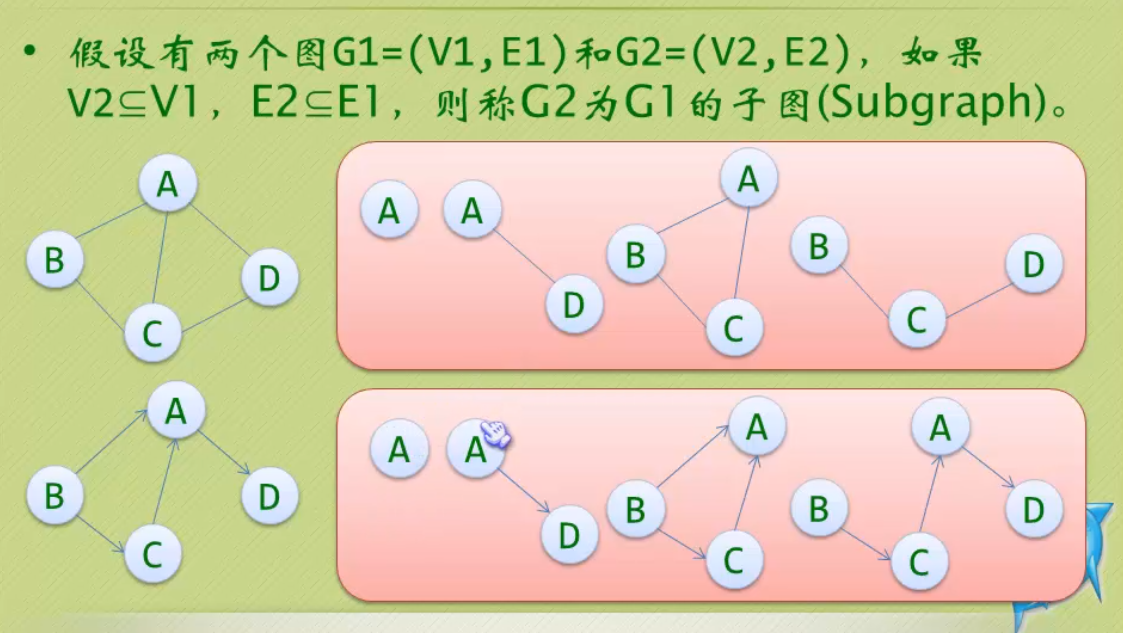
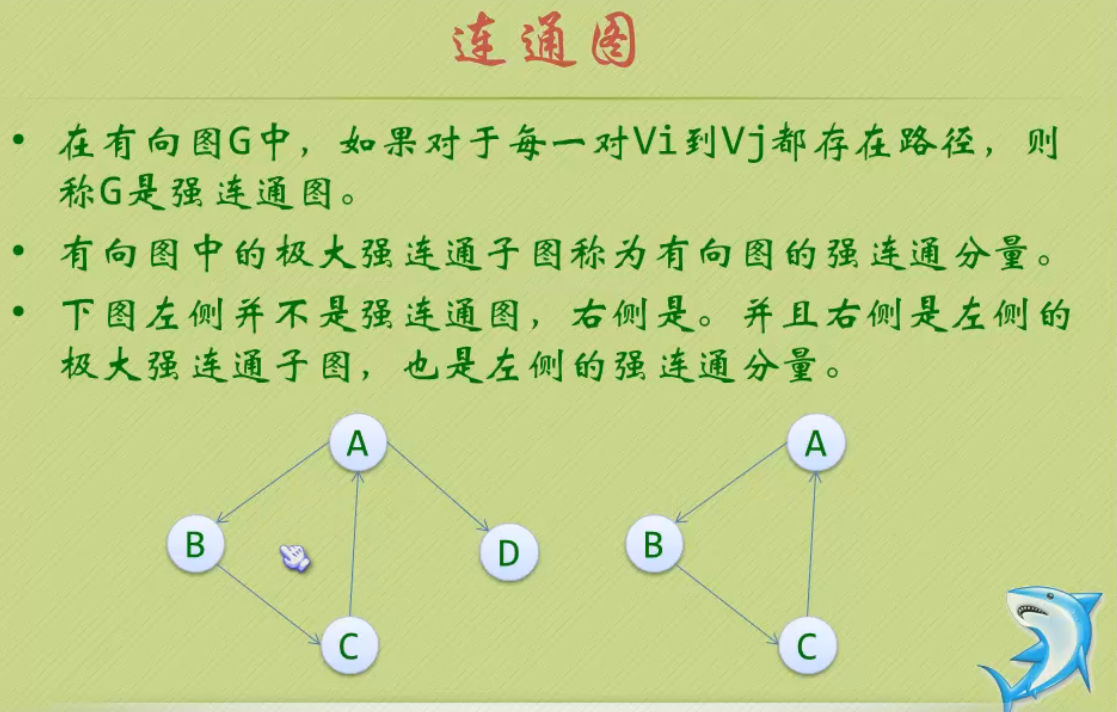
• 连通图的生成树定义：一个连通图的生成树是一个极小的连通子图，它含有图中全部的n个顶点，但只有足以构成一棵树的n-1条边。

• 

• 

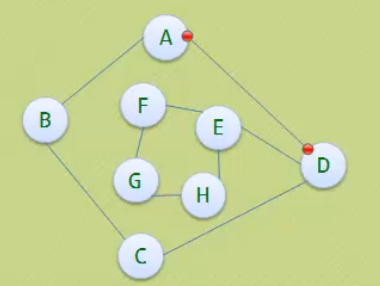
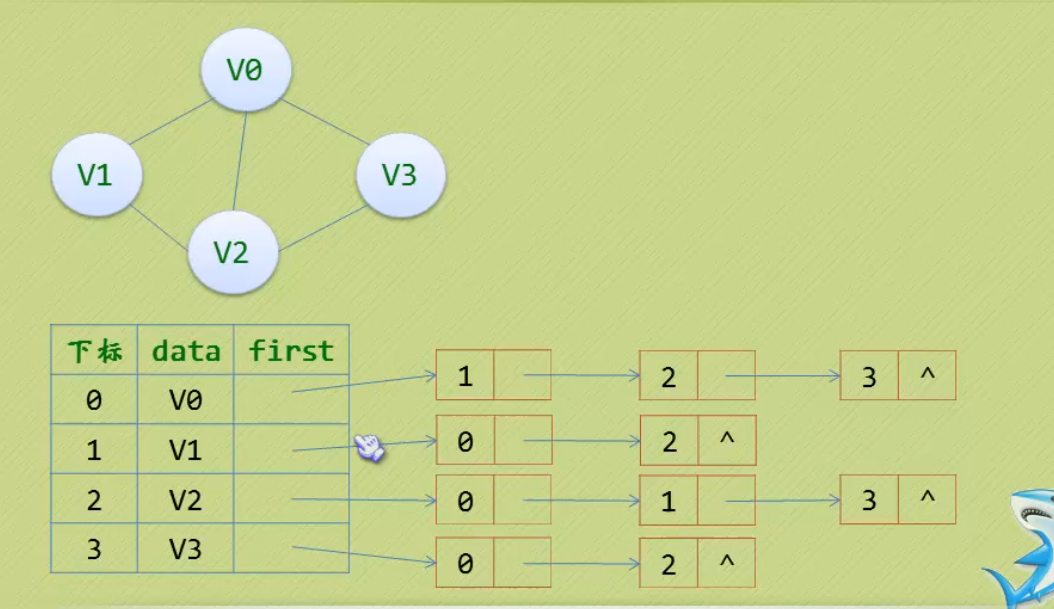
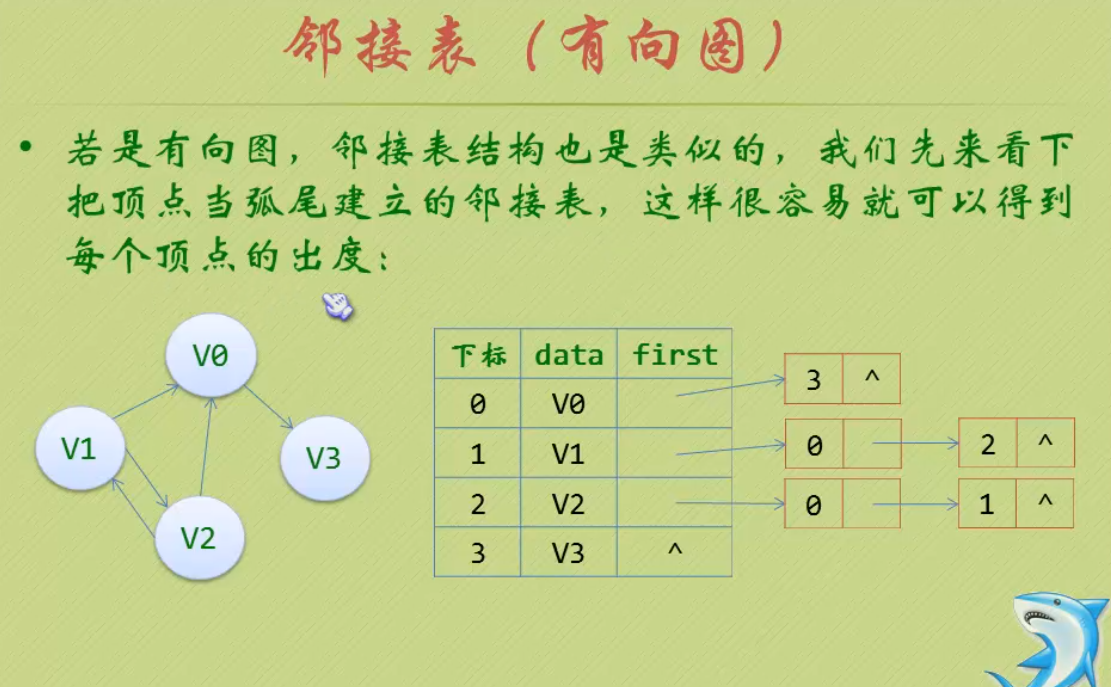
图的存储结构

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

马踏棋盘问题（骑士周游问题）

#include <stdio.h>
#include <time.h>

#define X 8
#define Y 8

int chess[X][Y];

// 找到基于(x,y)位置的下一个可走的位置
int nextxy(int *x, int *y, int count)
{
	switch(count)
	{
		case 0:
			if( *x+2<=X-1 && *y-1>=0 && chess[*x+2][*y-1]==0 )
			{
				*x = *x + 2;
				*y = *y - 1;
				return 1;
			}
			break;

		case 1:
			if( *x+2<=X-1 && *y+1<=Y-1 && chess[*x+2][*y+1]==0 )
			{
				*x = *x + 2;
				*y = *y + 1;
				return 1;
			}
			break;

		case 2:
			if( *x+1<=X-1 && *y-2>=0 && chess[*x+1][*y-2]==0 )
			{
				*x = *x + 1;
				*y = *y - 2;
				return 1;
			}
			break;

		case 3:
			if( *x+1<=X-1 && *y+2<=Y-1 && chess[*x+1][*y+2]==0 )
			{
				*x = *x + 1;
				*y = *y + 2;
				return 1;
			}
			break;

		case 4:
			if( *x-2>=0 && *y-1>=0 && chess[*x-2][*y-1]==0 )
			{
				*x = *x - 2;
				*y = *y - 1;
				return 1;
			}
			break;

		case 5:
			if( *x-2>=0 && *y+1<=Y-1 && chess[*x-2][*y+1]==0 )
			{
				*x = *x - 2;
				*y = *y + 1;
				return 1;
			}
			break;

		case 6:
			if( *x-1>=0 && *y-2>=0 && chess[*x-1][*y-2]==0 )
			{
				*x = *x - 1;
				*y = *y - 2;
				return 1;
			}
			break;

		case 7:
			if( *x-1>=0 && *y+2<=Y-1 && chess[*x-1][*y+2]==0 )
			{
				*x = *x - 1;
				*y = *y + 2;
				return 1;
			}
			break;

		default:
			break;
	}

	return 0;
}

void print()
{
	int i, j;

	for( i=0; i < X; i++ )
	{
		for( j=0; j < Y; j++ )
		{
			printf("%2d\t", chess[i][j]);
		}
		printf("\n");
	}
	printf("\n");
}

// 深度优先遍历棋盘
// (x,y)为位置坐标
// tag是标记变量，每走一步，tag+1
int TravelChessBoard(int x, int y, int tag)
{
	int x1=x, y1=y, flag=0, count=0;
	
	chess[x][y] = tag;

	// 如果tag==X*Y，则完成整个棋盘的遍历
	if( tag == X*Y )
	{
		print();
		return 1;
	}

	flag = nextxy(&x1, &y1, count);
	while( 0==flag && count < 7 )
	{
		count++;
		flag = nextxy(&x1, &y1, count);
	}

	while( flag )
	{
		if( TravelChessBoard(x1, y1, tag+1) )
		{
			return 1;
		}

		x1 = x;
		y1 = y;
		count++;

		flag = nextxy(&x1, &y1, count);
		while( 0==flag && count < 7 )
		{
			count++;
			flag = nextxy(&x1, &y1, count);
		}
	}

	if( 0 == flag )
	{
		chess[x][y] = 0;
	}

	return 0;
}

int main()
{
	int i, j;
	clock_t start, finish;

	start = clock();

	for( i=0; i < X; i++ )
	{
		for( j=0; j < Y; j++ )
		{
			chess[i][j] = 0;
		}
	}

	if( !TravelChessBoard(2, 0, 1) )
	{
		printf("抱歉，马踏棋盘失败鸟~\n");
	}

	finish = clock();
	printf("\n本次计算一共耗时: %f秒\n\n", (double)(finish-start)/CLOCKS_PER_SEC);

	return 0;
}

广度优先遍历

广度优先遍历(BreadthFirstSearch)，又称广度优先搜索，简称BFS。

//邻接矩阵的广度遍历算法
void BFSTraverse( MGraph G )
{
    int i, j;
    Queue Q;
    
    for( i=0; i < G.numVertexes;i++ )
    {
        visited[i] = FALSE;
    }
    
    initQueue( &Q );
    
    for( i=0; i<G.numVertexes; i++ )
    {
        if( !visited[i] )
        {
            printf("%c ", G.vex[i]);
            visited[i] = TRUE;
            EnQueue(&Q, i);
            
            while( !QueueEmpty(Q) )
            {
                DeQueue(&Q, &i);
                for( j = 0; j < G.numVertexes; j++ )
                {
                    if( G.art[i][j] == 1 && !visited[j] )
                    {
                        printf("%c ", G.vex[j]);
            			visited[j] = TRUE;
            			EnQueue(&Q, j);
                    }
                }
            }
        }
    }
}

Prim算法

考虑的出发点：为使生成树上边的权值之和达到最小，则应使生成树中每一条边的权值尽可能的小。

//Prim算法生成最小生成树
void MiniSpanTree_Prim(MGraph G)
{
    int min, i, j, k;
    int adjvex[MAXVEX];			//保存相关顶点下标
    int lowcost[MAXVEX];		//保存相关顶点间边的权值
    
    lowcost[0] = 0;				//V0作为最小生成树的根开始遍历，权值为0
    adjvex[0] = 0;				//V0第一个加入
    
    //初始化操作
    for(i = 1; j < G.numVertexes; i++ )
    {
        lowcost[i] = G.arc[0][i];		//将邻接矩阵第0行所有权值先加入数组
        adjvex[i] = 0;				//初始化全部先为V0的下标
    }
    
    //真正构造最小生成树的过程
    for(i=1; i < G.numVertexes; i++ )
    {
        min = INFINITY;		//初始化最小权值为65535等不可能数值
        j = 1;
        k = 0;
        
        //遍历全部顶点
        while( j < G.numVertexes )
        {
            //找出lowcost数组已存储的最小权值
            if( lowcost[j] != 0 && lowcost[j] < min )
            {
                min = lowcost[j];
                k = j; 			//将发现的最小权值的下标存入k，以待使用
            }
            j++;
        }
        
        //打印当前顶点边中权值最小的边
        printf("(%d, %d)", adjvex[k], k);
        lowcost[k] = 0;			//将当前顶点的权值设置为0，表示此顶点已完成任务，进行下一个顶点的遍历
        
        //邻接矩阵k行逐个遍历全部顶点
        for( j=1; j< G.numVertexes; j++ )
        {
            if( lowcost[j] != 0 && G.arc[k][j] < lowcost[j] )
            {
                lowcost[j] = G.arc[k][j];
                adjvex[j] = k;
            }
        }
    }
}

Kruskal算法生成最小生成树

//Kruskal算法生成最小生成树
int Find( int *parent, int f)
{
    while(parent[f] > 0 )
    {
        f = parent[f];
    }
    
    return f;
}

void MiniSpanTree_Kruskal(MGraph G)
{
    int i, n, m;
    Edge edges[MAGEDGE];		//定义边集数组
    int parent[MAXVEX];			//定义parent数组用来判断边与边是否形成环路
    
    for( i=0; i < G.numVertexes; i++ )
    {
        parent[i] = 0;
    }
    
    for( i=0; i < G.numEdges; i++ )
    {
        n = Find(parent, edges[i].begin);
        m = Find(parent, edges[i].end);
        
        if(n != m)		//如果n==m, 则形成环路，不满足
        {
            parent[n] = m;		//将此边的结尾顶点放入下标为起点的parent数组中，表示此顶点已经在生成树集合中
            printf("(%d, &d) %d ", edges[i].begin, edges[i].end, edges[i].weight);
        }
    }
}

迪杰斯特拉算法

#define MAXVEX 9
#define INFINITY 65535

typedef int Patharc[MAXVEX];			//用于存储最短路径下标的数组
typedef int ShortPathTable[MAXVEX];		//用于存储到各点最短路径的权值和

void ShortestPath_Dijkstar(MGraph G, int V0, Patharc *P, ShortPathTable *D)
{
    int v, w, k, min;
    int final[MAXVEX];		//final[w] = 1 表示已经求得顶点V0到Vw的最短路径
    
    //初始化数据
    for( v=0; v < G.numVertexes; v++ )
    {
        final[v] = 0;		//全部顶点初始化为未找到最短路径
        (*D)[V] = G.arc[V0][v];		//将与v0有连线的顶点加上权值
        (*P)[V] = 0;		//初始化路径数组P为0
    }
    
    (*D)[V0] = 0;		//v0至v0的路径为0
    final[V0] = 1;		//v0至v0不需要求路径
    
    //开始主循环，每次求得V0到某个v顶点的最短路径
    for( v=1; v < G.numVertexes; v++ )
    {
        min = INFINITY;
        for( w=0; w < G.numVertexes; w++ )
        {
            if( !final[w] && (*D)[w] < min )
            {
                k = w;
                min = (*D)[w];
            }
        }
        final[k] = 1;		//将目前找到的最近的顶点置1
        
        //修正当前最短路径及距离
        for( w=0; w < G.numVextes; w++ )
        {
            //如果经过v顶点的路径比现在这条路径的长度短的话，更新
            if( !final[w] && (min+G.arc[k][w] < (*D)[w]) )
            {
                (*D)[w] = min +G.arc[k][w];		//修改当前路径长度
                (*p)[w] = k;			//存放前驱顶点
            }
        }
    }
}

floyd算法

typedef int Pathmatrirx[MAXVEX][MAXVEX];
typedef int ShortPathTable[MAXVEX][MAXVEX];

void ShortestPath_Floyd(MGraph G, Pathmatrirx *P, ShortPathTable *D)
{
    int v, w, k;
    
    //初始化D和P
    for( v=0; v < G.numVertexes; v++ )
    {
        for( w=0; w < G.numVertexes; w++ )
        {
            (*D)[v][w] = G.matrix[v][w];
            (*P)[v][w] = w;
        }
    }
    
    //弗洛伊德算法
    for( k=0; k < G.numVertexes; k++ )
    {
        for( v=0; v < G.numVertexes; v++ )
        {
            for( w=0; w < G.numVertexes; w++ )
            {
                if( (*D)[v][w] > (*D)[v][k] + (*D)[k][w] )
                {
                    (*D)[v][w] = (*D)[v][k] + (*D)[k][w];
                    (*P)[v][w] = (*P)[v][k];		
                }
            }
        }
    }
}

拓扑排序

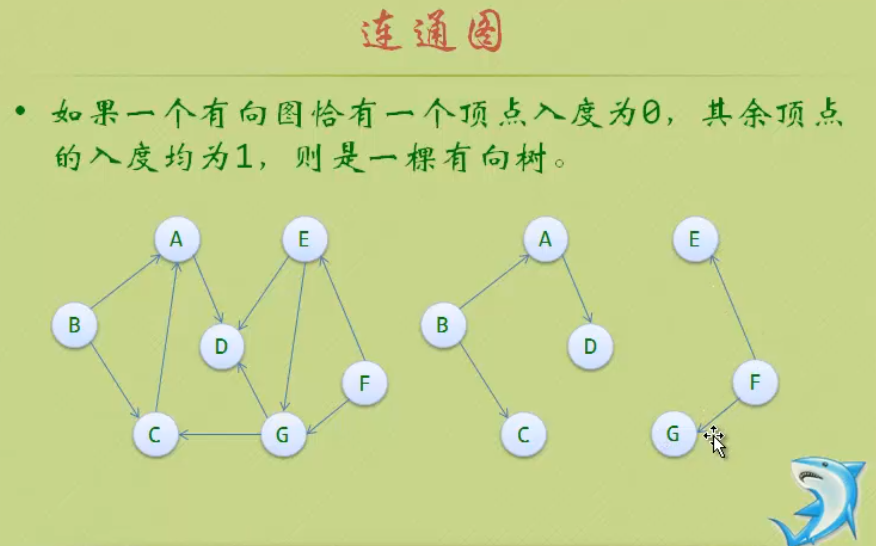
• 一个无环的有向图称为无环图（Directed Acyclic Graph)，简称DAG图。

• 在一个表示工程的有向图中，用顶点表示活动，用弧表示活动之间的优先关系，这样的有向图为顶点表示活动的网，称为AOV网(Active On Vertex Network)。

• // 边表结点声明
  typedef struct EdgeNode
  {
  	int adjvex;
  	struct EdgeNode *next;
  }EdgeNode;
  
  // 顶点表结点声明
  typedef struct VertexNode
  {
  	int in;			// 顶点入度
  	int data;
  	EdgeNode *firstedge;
  }VertexNode, AdjList[MAXVEX];
  
  typedef struct
  {
  	AdjList adjList;
  	int numVertexes, numEdges;
  }graphAdjList, *GraphAdjList;
  
  // 拓扑排序算法
  // 若GL无回路，则输出拓扑排序序列并返回OK，否则返回ERROR
  Status TopologicalSort(GraphAdjList GL)
  {
  	EdgeNode *e;
  	int i, k, gettop;
  	int top = 0;		// 用于栈指针下标索引
  	int count = 0;		// 用于统计输出顶点的个数
  	int *stack;			// 用于存储入度为0的顶点
  	
  	stack = (int *)malloc(GL->numVertexes * sizeof(int));
  	
  	for( i=0; i < GL->numVertexes; i++ )
  	{
  		if( 0 == GL->adjList[i].in )
  		{
  			stack[++top] = i;	// 将度为0的顶点下标入栈
  		}
  	}
  	
  	while( 0 != top )
  	{
  		gettop = stack[top--];	// 出栈
  		printf("%d -> ", GL->adjList[gettop].data);
  		count++;				
  		
  		for( e=GL->adjList[gettop].firstedge; e; e=e->next )
  		{
  			k = e->adjvex;
  			// 注意：下边这个if条件是分析整个程序的要点！
  			// 将k号顶点邻接点的入度-1，因为他的前驱已经消除
  			// 接着判断-1后入度是否为0，如果为0则也入栈
  			if( !(--GL->adjList[k].in) )	
  			{
  				stack[++top] = k;
  			}
  		}
  	}
  	
  	if( count < GL->numVertexes )	// 如果count小于顶点数，说明存在环
  	{
  		return ERROR;
  	}
  	else
  	{
  		return OK;
  	}
  }
  

关键路径

// 边表结点声明
typedef struct EdgeNode
{
	int adjvex;
	struct EdgeNode *next;
}EdgeNode;

// 顶点表结点声明
typedef struct VertexNode
{
	int in;			// 顶点入度
	int data;
	EdgeNode *firstedge;
}VertexNode, AdjList[MAXVEX];

typedef struct
{
	AdjList adjList;
	int numVertexes, numEdges;
}graphAdjList, *GraphAdjList;

int *etv, *ltv;
int *stack2;			// 用于存储拓扑序列的栈
int top2;				// 用于stack2的栈顶指针

// 拓扑排序算法
// 若GL无回路，则输出拓扑排序序列并返回OK，否则返回ERROR
Status TopologicalSort(GraphAdjList GL)
{
	EdgeNode *e;
	int i, k, gettop;
	int top = 0;		// 用于栈指针下标索引
	int count = 0;		// 用于统计输出顶点的个数
	int *stack;			// 用于存储入度为0的顶点
	
	stack = (int *)malloc(GL->numVertexes * sizeof(int));
	
	for( i=0; i < GL->numVertexes; i++ )
	{
		if( 0 == GL->adjList[i].in )
		{
			stack[++top] = i;	// 将度为0的顶点下标入栈
		}
	}
	
	// 初始化etv都为0
	top2 = 0;
	etv = (int *)malloc(GL->numVertexes*sizeof(int));
	for( i=0; i < GL->numVertexes; i++ )
	{
		etv[i] = 0;
	}
	stack2 = (int *)malloc(GL->numVertexes*sizeof(int));
	
	while( 0 != top )
	{
		gettop = stack[top--];		// 出栈
		// printf("%d -> ", GL->adjList[gettop].data); 
		stack2[++top2] = gettop;	// 保存拓扑序列顺序 C1 C2 C3 C4 .... C9
		count++;				
		
		for( e=GL->adjList[gettop].firstedge; e; e=e->next )
		{
			k = e->adjvex;
			// 注意：下边这个if条件是分析整个程序的要点！
			// 将k号顶点邻接点的入度-1，因为他的前驱已经消除
			// 接着判断-1后入度是否为0，如果为0则也入栈
			if( !(--GL->adjList[k].in) )	
			{
				stack[++top] = k;
			}
			
			if( (etv[gettop]+e->weight) > etv[k] )
			{
				etv[k] = etv[gettop] + e->weight;
			}
		}
	}
	
	if( count < GL->numVertexes )	// 如果count小于顶点数，说明存在环
	{
		return ERROR;
	}
	else
	{
		return OK;
	}
}

// 求关键路径，GL为有向图，输出GL的各项关键活动
void CriticalPath(GraphAdjList GL)
{
	EdgeNode *e;
	int i, gettop, k, j;
	int ete, lte;
	
	// 调用改进后的拓扑排序，求出etv和stack2的值
	TopologicalSort(GL);
	
	// 初始化ltv都为汇点的时间
	ltv = (int *)malloc(GL->numVertexes*sizeof(int));
	for( i=0; i < GL->numVertexes; i++ )
	{
		ltv[i] = etv[GL->numVertexes-1];
	}
	
	// 从汇点倒过来逐个计算ltv
	while( 0 != top2 )
	{
		gettop = stack2[top2--];	// 注意，第一个出栈是汇点
		for( e=GL->adjList[gettop].firstedge; e; e=e->next )
		{
			k = e->adjvex;
			if( (ltv[k] - e->weight) < ltv[gettop] )
			{
				ltv[gettop] = ltv[k] - e->weight;
			}
		}
	}
	
	// 通过etv和ltv求ete和lte
	for( j=0; j < GL->numVertexes; j++ )
	{
		for( e=GL->adjList[j].firstedge; e; e=e->next )
		{
			k = e->adjvex;
			ete = etv[j];
			lte = ltv[k] - e->weight;
			
			if( ete == lte )
			{
				printf("<v%d,v%d> length: %d , ", GL->adjList[j].data, GL->adjList[k].data, e->weight );
			}
		}
	}
}

插值查找(按比例查找)

要求：待查序列按关键码有序。基本思想：先确定待查记录所在的区间，然后逐步缩小范围直到找到或找不到该记录为止。折半查找要求线性表用顺序表作为存储结构。

int Search_Bin(int a[], int n, int target)//a[0]不用，a[1]~a[n]存储数据
{
    int low = 1;
    int high = n;
    while(low <= high)
    {
        int mid = low + (high - low) / 2;
        if(a[mid] == target) return mid;
        else if(a[mid] > target) high = mid - 1;
        else low = mid + 1;
    }
    return 0;
}

斐波那契查找(黄金分割法查找)

public static int MaxSize=20;  //先为斐波那契数列设置长度
    //构建你波拉契数列
    public static int[] fib(){
        int[] f=new int[MaxSize];
        f[0]=1;
        f[1]=1;
        for (int i=2;i<MaxSize;i++){
            f[i]=f[i-1]+f[i-2];
        }
        return f;
    }

public static int fibSearch(int[] arr,int key){
        int left=0;  //初始指向最数组最左边
        int right=arr.length-1; //初始指向最数组最右边
        int k=0;  //指示斐波那契数列的下标，初始为0是为了根据数组长度确定数组需要扩展的长度
        int mid=0;
        int[] f=fib(); //获取斐波那契数列
        while (arr.length>f[k]-1){ //这里的f[k]是arr距离斐波那契数列最近的数值，为什么-1，为了符合数组特性(数组最大元素下标是数组长度-1)
            k++;
        }
        int[] temp=Arrays.copyOf(arr,f[k]); //为什么构建一个新数组，因为下面需要对数组进行扩展，查找最后还要用到原始数组，所以不能用原始数组
        //扩展数组
        for (int i=right+1;i<temp.length;i++){  //这里为什么用temp.length?因为上面Arrays.copyOf(arr,f[k])已经对数组扩展了，这里我们进行的是把扩展的值都改为原始数组的最大值
            temp[i]=arr[right];
        }

        while (left<=right){
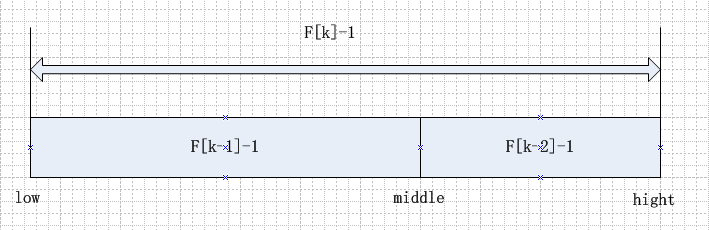
            mid=left+f[k-1]-1;   //这里就是为mid确定位置，位置确定请看上面的图
            if (key<temp[mid]){  //如果当前mid值大于key，说明key在mid左边部分，继续对左边的F[k-1]-1部分进行分割
                right=mid-1;
                k--;
            }else if (key>temp[mid]){
                left=mid+1;
                k-=2;
            }else {
                if (mid<arr.length){ //查找值的下标在arr数组额范围内，直接返回
                    return mid;
                }else { //不在就返回right,为什么？因为后面几位的值和right的值是一样的，说明查找的值就是right
                    return right;
                }
            }
        }
        //都找不到返回-1
        return -1;

    }

public static void main(String[] args) {
        int[] a={0,16,24,35,47,59,62,73,88,99};
        int key=99;
        System.out.println(fibSearch(a,key));
    }

线性索引查找

二叉排序树

//二叉树的查找
//二叉树的二叉链表结点结构定义

typedef struct BiTNode
{
    int data;
    struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

//递归查找二叉排序树T中是否存在key
//指针f指向T的双亲，其初始值调用值为NULL
//若查找成功，则指针p指向该数据元素结点，并返回TRUE
//否则指针p指向查找路径上访问的最后一个结点，并返回FALSE
Status SearchBST(BiTree T, int key, BiTree f, BiTree *p)
{
    if(!T)	//查找不成功
    {
        *p = f;
        return FALSE;
    }
    else if( key == T->data)		//查找成功
    {
        *p = T;
        return TRUE;
    }
    else if( key < T->data)
    {
        return SearchBST( T->lchild, key, T, p );		//在左子树继续查找
    }
    else
    {
        return SearchBST( T->rchild, key, T, p );		//在右子树继续查找
    }
}

//二叉树的插入
//当二叉排序树T中不存在关键字等于key的数据元素时，
//插入key并返回TRUE，否则返回FALSE
Status InsertBST(BiTree *T, int key)
{
    BiTree p, s;
    if( !SearchBST(*T, key, NULL, &p))
    {
        s = (BiTree)malloc(sizeof(BiTNode));
        s->data = key;
        s->lchild = s->rchild = NULL;
        
        if( !p )		//查找不到key
        {
            *T = s;		//插入s为新的根结点
        }
        else if( key < p->data )
        {
            p->lchild = s;		//插入s为左孩子
        }
        else
        {
            p->rchild = s;		//插入s为右孩子
        }
        return TRUE;
    }
    else
    {
        return FALSE;		//树中已有关键字相同的结点，不再插入
    }
}

//删除二叉树
Status DeleteBST(BiTree *T, int key)
{
    if( !*T )
    {
        return FALSE;
    }
    else
    {
        if( key == (*T)->data )
        {
            return Delete(T);
        }
        else if( key < (*T)->data )
        {
            return DeleteBST(&(*T)->lchild, key);
        }
        else
        {
            return DeleteBST(&(*T)->rchild, key);
        }
    }
}

Status Delete(BiTree *p)
{
    BiTree q, s;
    
    if( (*p)->rchild == NULL )
    {
        q = *p;
        *p = (*p)->lchild;
        free(q);
    }
    else if((*p) ->lchild == NULL )
    {
        q = *p;
        *p = (*p)->rchild;
        free(q);
    }
    else
    {
        q = *p;
        s = (*p)->lchild;
        
        while( s->rchild )
        {
            q = s;
            s = s->rchild;
        }
        
        (*p)->data = s->data;
        
        if( q != *p)
        {
            q->rchild = s->lchild;
        }
        else
        {
            q->lchild = s->lchild;
        }
        
        free(s);
    }
    
    return TRUE;
}

平衡二叉树

//AVL

#define LH 1
#define EH 0
#define RH -1
typedef struct BiTNode
{
    int data;
    int bf;
    struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;

void R_Rotate(BiTree *p)
{
    BiTree L;
    L = (*p)->lchild;
    (*p)->lchild = L->rchild;
    L->rchild = (*p);
    *p = L;
}

void LeftBalance(BiTree *T)
{
    BiTree L, Lr;
    L = (*T)->lchild;
    
    switch(L->bf)
    {
        case LH:
            (*T)->bf = L->bf = EH;
            R_Rotate(T);
            break;
        case RH:
            Lr = L->rchild;
            switch(Lr->bf)
            {
                case LH:
                    (*T)->bf = RH;
                    L->bf = EH;
                    break;
                case EH:
                    (*T)->bf = L->bf = EH;
                    break;
                case RH:
                    (*T)->bf = EH;
                    L->bf = LH;
                    break;
            }
            Lr->bf = EH;
            L_Rotate(&(*T)->lchild);
            R_Rotate(T);
            break;
    }
}

int InsertAVL(BiTree *T, int e, int *taller)
{
    if( !*T )
    {
        *T = (BiTree)malloc(sizeof(BiTNode));
        (*T)->data = e;
        (*T)->lchild = (*T)->rchild = NULL;
        (*T)->bf = EH;
        *taller = TRUE;
    }
    else
    {
        if(e == (*T)->data)
        {
            *taller = FALSE;
            return FALSE;
        }
        if(e < (*T)->data)
        {
            if(!InsertAVL(&(*T)->lchild, e, taller))
            {
                return FALSE;
            }
            if(*taller)
            {
                switch((*T)->bf)
                {
                    case LH:
                        LeftBalance(T);
                        *taller = FALSE;
                        break;
                    case EH:
                        (*T)->bf = LH;
                        *taller = FALSE;
                        break;
                    case RH:
                        (*T)->bf = EH;
                        *taller = FALSE;
                        break;
                }
            }
        }
        else
        {
            if(!InsertAVL(&(*T)->rchild, e, taller))
            {
                return FALSE;
            } 
             if(*taller)
            {
                switch((*T)->bf)
                {
                    case LH:
                        (*T)->bf = EH;
                        *taller = FALSE;
                        break;
                    case EH:
                        (*T)->bf = RH;
                        *taller = TRUE;
                        break;
                    case RH:
                        RightBalance(T);
                        *taller = FALSE;
                        break;
                }
        }
            
    }
}

散列表(哈希表)查找

• 散列表的查找步骤：
  • 当存储记录时，通过散列函数计算出记录的散列地址。
  • 当查找记录时，我们通过同样的是散列函数计算记录的散列地址，并按此散列地址访问该记录。