数据结构与算法(三)
双向链表
链表由单向的链变成双向链,使用这种数据结构,我们不再拘束于单链表的单向创建于遍历等操作。

在单链表中,有一个数据域,还有一个指针域,数据域用来存储相关数据,而指针域负责链表之间的“联系”。在双向链表中,需要有两个指针域,一个负责向后连接,一个负责向前连接。
//单链表的结构
struct List{
int data; //数据域
struct List *next; //指针域
};
//双向链表的结构
typedef struct List{
int data; //数据域
struct List *next; //向后的指针
struct Lsit *front; //向前的指针
};
typedef struct List* pElem;
typedef struct List eElem;
同单链表一样,对双向链表的操作也有创建,插入,遍历,删除,销毁。
双向链表的创建
在创建双向链表的时候,需要初始化两个指针。同单链表一样,需要一个头指针来标志链表的信息。可以写出该函数的定义:
pElem CreateList(){
pElem head = (pElem)malloc( sizeof(eElem) );
assert(head != NULL ); //包含于标准库<assert.h>
head -> next = head -> front = NULL; //初始化链表,指针置空
return head;
}
双向链表的插入
在单向链表的头插法中,最主要的语句就是tmp->next = head->next,而在双向链表中,多了一个向前的指针。
void InsertElem( pElem head, int data ){
if ( head == NULL ){
printf("The list is empty.\n"); //头结点为空,无法插入
return;
}
pElem tmpHead = head; //创建一个临时的头结点指针
if( tmpHead->next ==NULL ){
//当双向链表只有一个头结点时
pElem addition = (pElem)malloc( sizeof(eElem) );
assert( addition != NULL );
addition->data = data; //数据域赋值
addition->next = tmpHead->next; //后向指针连接
tmpHead->next = addition;
addition->front = tmpHead; //将插入结点的front指向头结点
}
else{
//当双向链表不只一个头结点时
pElem addition = (pElem)malloc( sizeof(eElem) );
assert( addition != NULL );
addition -> data = data; //数据域赋值
tmpHead->next->front = addition; //头结点的下一个结点的front指针
addition->front = tmpHead; //插入的结点的front指针指向头结点
addition->next = tmpHead->next; //插入结点的next 指针指向原本头指针的下个结点
tmpHead->next = addition; //将头结点的next指针指向插入结点
}
}
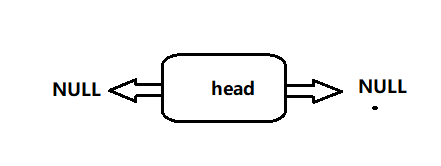
创建一个新的结点addition,此时表中只有头结点,因此执行if中的程序,执行完毕后就变成了:
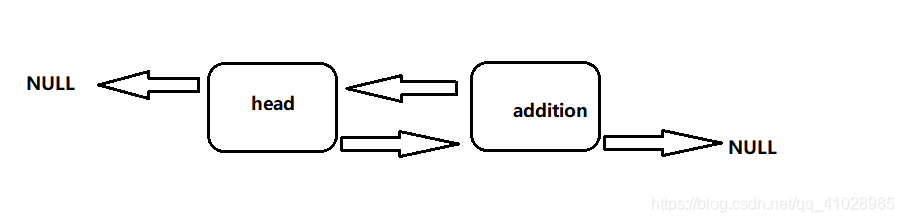
双向链表的遍历
在遍历中将实现next的向后遍历,也会实现front的向前遍历
void IlluList( pElem head ){
printf("-----------------------------\n");
if( head == NULL ){
printf("The list is empty.\n");
return;
}
pElem tmpHead = head;
while( tmpHead->next != NULL ){
tmpHead = tmpHead->next; //头结点数据为空,因此直接从头结点的下一结点开始遍历
printf("%d\n", tmpHead->data);
}
//此时tmpHead的地址在链表的最后一个结点处
while( tmpHead->front->front != NULL ){
printf("%d\n", tmpHead->data); //最后一个结点要输出
tmpHead = tmpHead->front;
}
printf("%d\n", tmpHead->data);
return;
}
当向后遍历完成之后,此时tmpHead的地址是链表的最后一个结点的地址,因此使用front来进行向前的遍历,如果判断条件是tmpHead->front !=NULL的话,会将头结点的数据域也输出,然而头结点的数据域未使用,因此会输出一个不确定的值。正因此判断条件改为tmpHead->front->front !=NULL
删除一个结点
当删除一个结点的时候,我们要判断在链表中是否存在与之匹配的结点,有的话删除成功,否则失败。
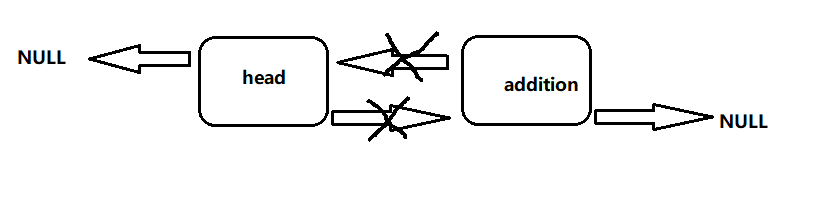
就像这幅图一样,当删除addition结点时,先讲addition的下一个结点与head相连,而下一个结点是NULL,因此可以得出函数为:
void DeleteElem( pElem head, int data ){
if( head == NULL ){
printf("The list is empty.\n");
return;
}
pElem tmpHead = head;
while( tmpHead->next != NULL ){
tmpHead = tmpHead->next;
if( tmpHead->data == data ){
tmpHead->front->next = tmpHead->next; //将被删结点的上一个结点的next指针指向被删结点的下一个结点
tmpHead->next->front = tmpHead->front; //将被删结点的下一个结点front指针指向被删结点的上一个结点
break;
}
}
free(tmpHead); //释放内存
}
销毁链表
销毁一个双向链表的操作同单链表的相似。指针不断向后运动,每运动一个结点,释放上一个结点。
void DestroyList( pElem head ){
pElem tmp;
while( head->next != NULL ){
tmp = head; //指针不断后移
head = head->next;
free(tmp);
}
free(head);
}

此时,tmp的地址就是head的地址,但当执行一个之后,就变成这样。
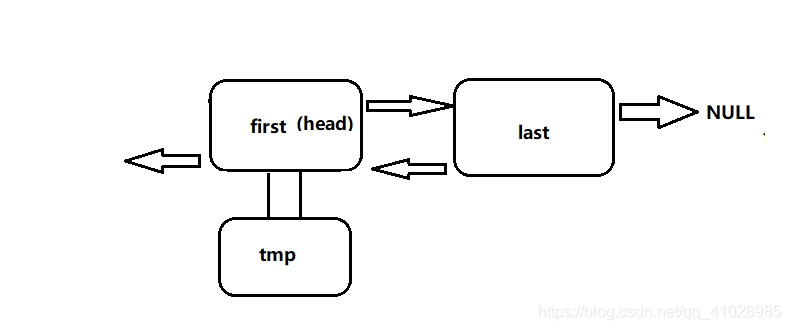
上一次执行完之后,头结点已经被释放,此时头结点就在第一个数据结点处。以此往后,最后循环结束,释放最后一个结点。
课堂演示题目
要求实现用户输入一个数使得26个字母的排列发生变化,例如用户输入3,输出结果:
- DEFGHIJKLMNOPQRSTUVWXYZABC
同时需要支持负数,例如用户输入-3,输出结构:
-
XYZABCDEFGHIJKLMNOPQRSTUVW
#include <stdio.h> #include <stdlib.h> #define OK 1 #define ERROR 0 typedef char ElemType; typedef int Status; typedef struct DualNode { ElemType data; struct DualNode *prior; struct DualNode *next; }DualNode, *DuLinkList; Status InitList(DuLinkList *L) { DualNode *p, *q; int i; *L = (DuLinkList)malloc(sizeof(DualNode)); if( !(*L) ) { return ERROR; } (*L)->next = (*L)->prior = NULL; p = (*L); for( i=0; i < 26; i++ ) { q = (DualNode *)malloc(sizeof(DualNode)); if( !q ) { return ERROR; } q -> data = 'A'+i; q -> prior = p; q -> next = p -> next; p -> next = q; p = q; } p->next = (*L)->next; (*L)->next->prior = p; return OK; } void Caesar(DuLinkList *L, int i) { if( i > 0 ) { do { (*L) = (*L)->next; }while( --i ); } if( i < 0 ) { do { (*L) = (*L)->next; }while( ++i ); } } int main() { DuLinkList L; int i, n; InitList(&L); printf("请输入一个整数:"); scanf("%d", &n); printf("\n"); Caesar(&L, n); for( i=0; i < 26; i++ ) { L = L->next; printf("%c", L->data); } printf("\n"); return 0; }
栈和队列
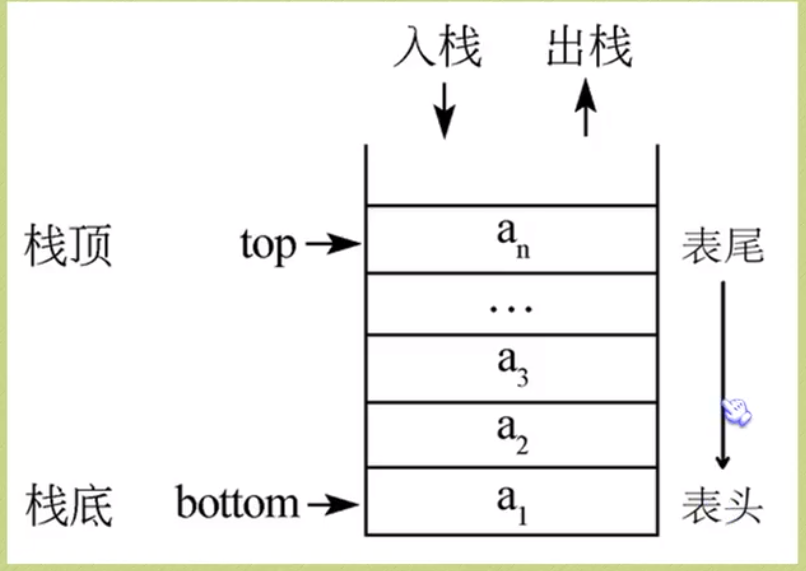
栈:(Stack)是一个后进先出(Last in first out ,LIFO)的线性表,它要求只在表尾进行删除和插入操作。
对于栈来说,表尾称为栈的栈顶(top),相应的表头称为栈底(bottom)。
栈的顺序存储结构
typedef struct
{
ElemType *base;
ElemType *top;
int stackSize;
}sqStack;
base是指向栈底的指针变量,top是指向栈顶的指针变量,stackSize指示栈的当前可使用的最大容量。
创建一个栈
#define STACK_INIT_SIZE 100
initStack(sqStack *s)
{
s -> base = (ElemType *)malloc(STACK_INIT_SIZE * sizeof(ElemType) );
if( !s->base )
exit(0);
s -> top = s -> base; //最开始,栈顶就是栈底
s -> stackSize = STACK_INIT_SIZE;
}
入栈操作
- 入栈操作也叫压栈操作,就是向栈中存放数据
- 入栈操作要在栈顶进行,每次向栈中压入一个数据,top指针就要+1,直到栈满为止。
#define STACKINCREMENT 10
Push(sqStack *s, ElemType e)
{
//如果栈满,追加空间
if( s->top - s->base >= s->stackSize )
{
s->base = (ElemType *)realloc(s->base, (s->stackSize + STACKINCREMENT) * sizeof(ElemType));
if( !s->base )
exit(0);
s->top = s->base + s->stackSize; //设置栈顶
s->stackSize = s->stackSize + STACKINCREMENT; //设置栈的最大容量
}
*(s->top) = e;
s->top++;
}
出栈操作
-
出栈操作就是在栈顶取出数据,栈顶指针随之下移的操作
-
每当从栈内弹出一个数据,栈的当前容量就-1
Pop(sqStack *s, ElemType *e) { if( s->top == s->base ) //栈已空 return; *e = *--(s->top); }
清空一个栈
-
将栈中的元素全部作废,栈本身的物理空间并不发生改变。
-
只要将s->top的内容赋值为s->base即可,这样s->base等于s->top,也就表明这个栈是空的。
ClearStack(sqStack *s){ s->top = s->base; }
销毁一个栈
-
销毁一个栈与清空一个栈不同,销毁一个栈是要释放掉该栈所占据的物理内存空间。
DestroyStack(sqStack *s){ int i, len; len = s->stackSize; for( i=0; i < len; i++ ){ free( s->base ); s->base++; } s->base = s->top = NULL; s->stackSize = 0; }
计算栈的当前容量
-
计算栈的当前容量也就是计算栈中元素的个数,因此只要返回s.top - s.base即可
-
注:栈的最大容量是指该栈占据内存空间的大小,其值时s.stackSize, 它与栈的当前容量不是一个概念。
int StackLen(sqStack s) { return (s.top - s.base ); }
实例分析
-
题目:利用栈的数据结构特点,将二进制转换为十进制数。
#include <stdio.h> #include <stdlib.h> #include <math.h> #define STACK_INIT_SIZE 20 #define STACKINCREMENT 10 typedef char ElemType; typedef struct { ElemType *base; ElemType *top; int stackSize; }sqStack; void InitStack(sqStack *s) { s->base = (ElemType *)malloc(STACK_INIT_SIZE * sizeof(ElemType)); if( !s->base ) { exit(0); } s->top = s->base; s->stackSize = STACK_INIT_SIZE; } void Push(sqStack *s, ElemType e) { if( s->top - s->base >= s->stackSize ) { s->base = (ElemType *)realloc(s->base, (s->stackSize + STACKINCREMENT) * sizeof(ElemType) ); if( !s->base ) { exit(0); } } *(s->top) = e; s->top++; } void Pop(sqStack *s, ElemType *e) { if( s->top == s->base ) { return; } *e = *--(s->top); } int StackLen(sqStack s) { return (s.top - s.base); } int main() { ElemType c; sqStack s; int len, i, sum = 0; InitStack(&s); printf("请输入二进制数,输入#符号表示结束!\n"); scanf("%c", &c); while( c != '#' ) { Push(&s, c); scanf("%c", &c); } getchar(); //把'\n'从缓冲区去掉 len = StackLen(s); printf("栈的当前容量是:%d\n", len); for(i = 0; i < len; i++ ) { Pop(&s, &c); sum = sum + (c-48) * pow(2, i); } printf("转化为十进制数是:%d\n", sum); return 0; }
栈的链式存储结构
- 栈因为只是栈顶来做插入和删除操作,所以比较好的方法就是将栈顶放在单链表的头部,栈顶指针和单链表的头指针合二为一。
进栈操作
对于栈链的Push操作,假设元素值为e的新结点是s,top为栈顶指针
Status Push(LinkStack *s, ElemType e)
{
LinkStackPtr p = (LinkStackPtr) malloc (sizeof(StackNode));
p->data = e;
p->next = s->top;
s->top = p;
s->count++;
return OK;
}
出栈操作
假设变量p用来存储要删除的栈顶结点,将栈顶指针下移一位,最后释放p即可
Status Pop(LinkStack *s, ElemType *e )
{
LinkStackPtr p;
if( StackEmpty(*s)) //判断是否为空栈
return ERROR;
*e = s->top->data;
p = s->top;
s->top = s->top->next;
free(p);
s->count--;
return OK;
}
(重点)逆波兰计算器
- 实现对逆波兰输入的表达式进行计算
- 支持带小数点的数据
- 正常表达式----------->逆波兰表达式
- a+b-------------->a b +
- a+(b-c) --------------------> a b c - +
- a+(b-c)*d --------------------> a b c - d * +
- a+d*(b-c)-----------------> a d b c - * +
#include <stdio.h>
#include <ctype.h>
#include <stdlib.h>
#define STACK_INIT_SIZE 20
#define STACKINCREMENT 10
#define MAXBUFFER 10
typedef double ElemType;
typedef struct
{
ElemType *base;
ElemType *top;
int stackSize;
}sqStack;
InitStack(sqStack *s)
{
s->base = (ElemType *)malloc(STACK_INIT_SIZE * sizeof(ElemType));
if( !s->base )
exit(0);
s->top = s->base;
s->stackSize = STACK_INIT_SIZE;
}
Push(sqStack *s, ElemType e)
{
// 栈满,追加空间,鱼油必须懂!
if( s->top - s->base >= s->stackSize )
{
s->base = (ElemType *)realloc(s->base, (s->stackSize + STACKINCREMENT) * sizeof(ElemType));
if( !s->base )
exit(0);
s->top = s->base + s->stackSize;
s->stackSize = s->stackSize + STACKINCREMENT;
}
*(s->top) = e; // 存放数据
s->top++;
}
Pop(sqStack *s, ElemType *e)
{
if( s->top == s->base )
return;
*e = *--(s->top); // 将栈顶元素弹出并修改栈顶指针
}
int StackLen(sqStack s)
{
return (s.top - s.base);
}
int main()
{
sqStack s;
char c;
double d, e;
char str[MAXBUFFER];
int i = 0;
InitStack( &s );
printf("请按逆波兰表达式输入待计算数据,数据与运算符之间用空格隔开,以#作为结束标志: \n");
scanf("%c", &c);
while( c != '#' )
{
while( isdigit(c) || c=='.' ) // 用于过滤数字
{
str[i++] = c;
str[i] = '\0';
if( i >= 10 )
{
printf("出错:输入的单个数据过大!\n");
return -1;
}
scanf("%c", &c);
if( c == ' ' )
{
d = atof(str);
Push(&s, d);
i = 0;
break;
}
}
switch( c )
{
case '+':
Pop(&s, &e);
Pop(&s, &d);
Push(&s, d+e);
break;
case '-':
Pop(&s, &e);
Pop(&s, &d);
Push(&s, d-e);
break;
case '*':
Pop(&s, &e);
Pop(&s, &d);
Push(&s, d*e);
break;
case '/':
Pop(&s, &e);
Pop(&s, &d);
if( e != 0 )
{
Push(&s, d/e);
}
else
{
printf("\n出错:除数为零!\n");
return -1;
}
break;
}
scanf("%c", &c);
}
Pop(&s, &d);
printf("\n最终的计算结果为:%f\n", d);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号