隐函数微分法 --> 逆函数求导 --> 指数、对数函数求导 --> 对数微分法

1. 隐函数微分法

考虑这种情况，\(x\)和\(y\)之间存在某种关系，例如：\(x^2 + y^2 = 1\)。常规的是将\(y\)表示为\(x\)的函数后，然后根据导数的定义进行求导，如下：

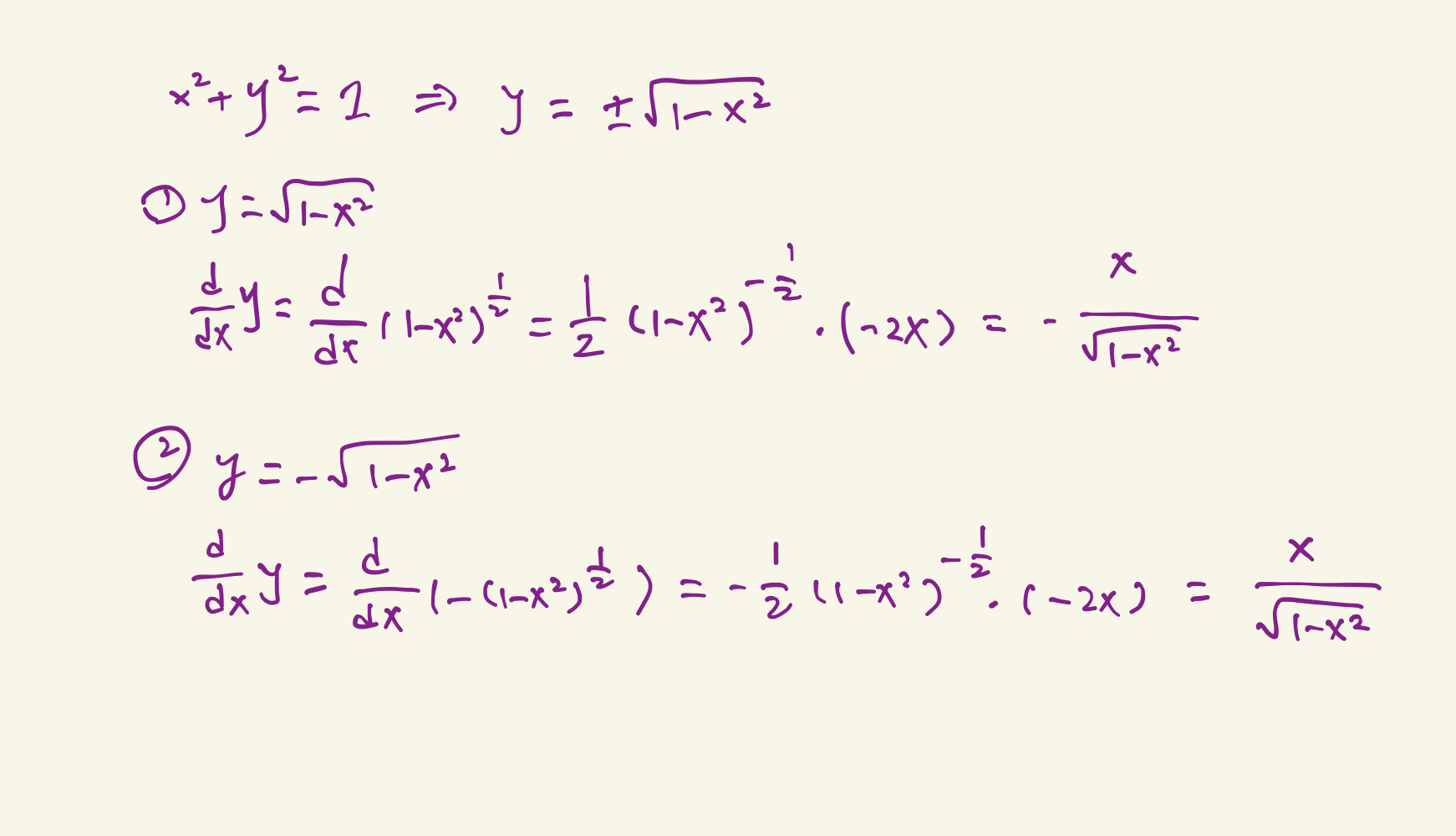
这种求导是及其不方便的，所以我们有隐函数微分法

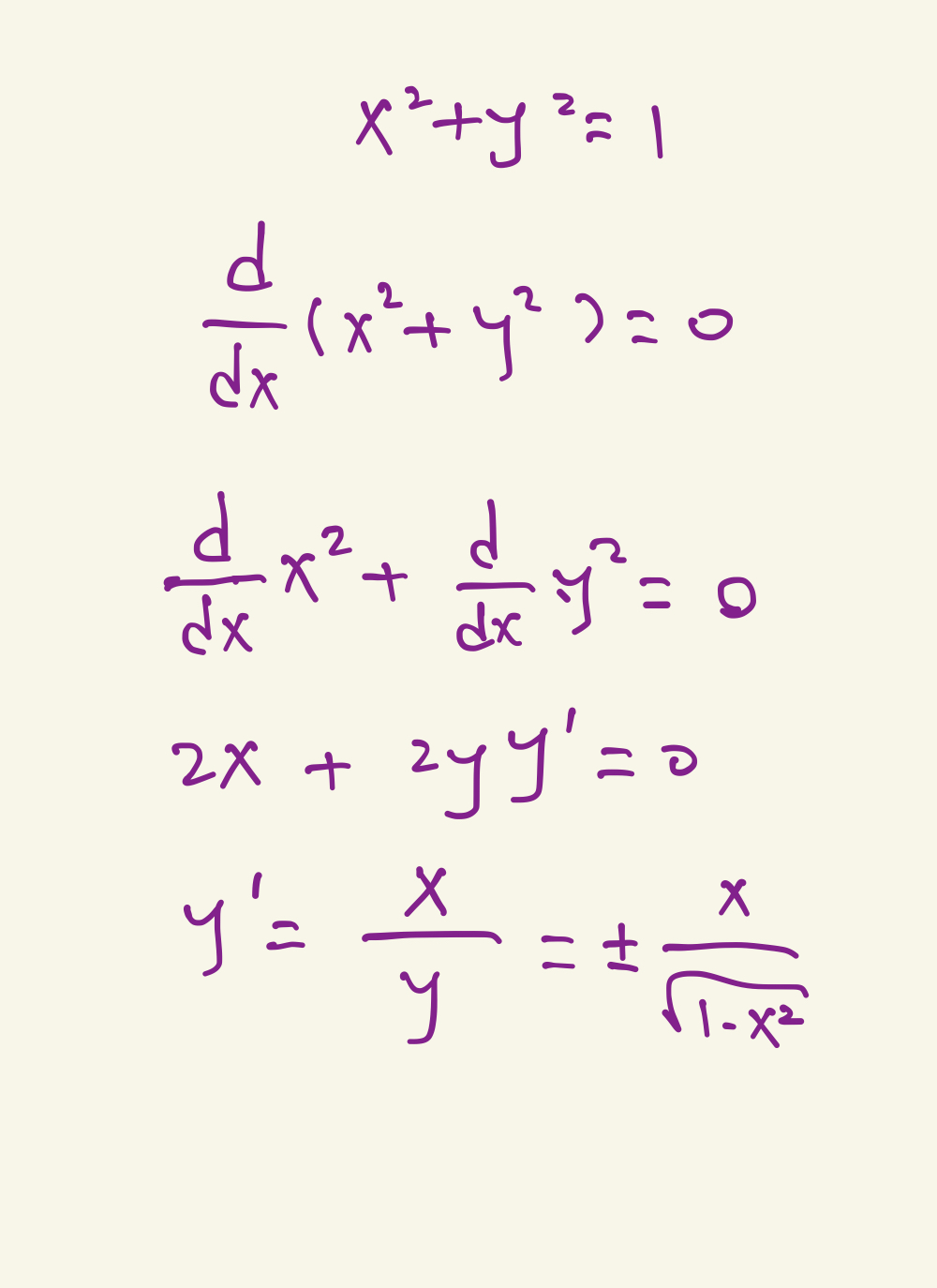
我们直接对等式两边同时求导即可

2. 逆函数求导

考虑这种情况，我们需要对一个函数求导，但是我们发现直接对其求导有困难，但是对其逆函数求导却是简单的，所以我们只要找出逆函数的导数和原函数导数之间的关系即可

举个例子：

3. 指数、对数的求导

先看指数函数的求导，然后再引到对数的求导

现在，我们需要对 \(M(a)\) 进行处理。我们引入 \(e\) ，我们让 \(M(e) = 1\)

现在我们来讨论一下 \(e\) 存在的合理性

到了这里，关于指数函数的求导我们还有一块 \(M(a)\)

为了解决这一点，我们来看对数

有了这点，我们回到最初的 \(\frac{d}{dx} a^{x} = a^xM(a)\)

对于 \(a^x\) 的求导，有两种方式，第一种如下：

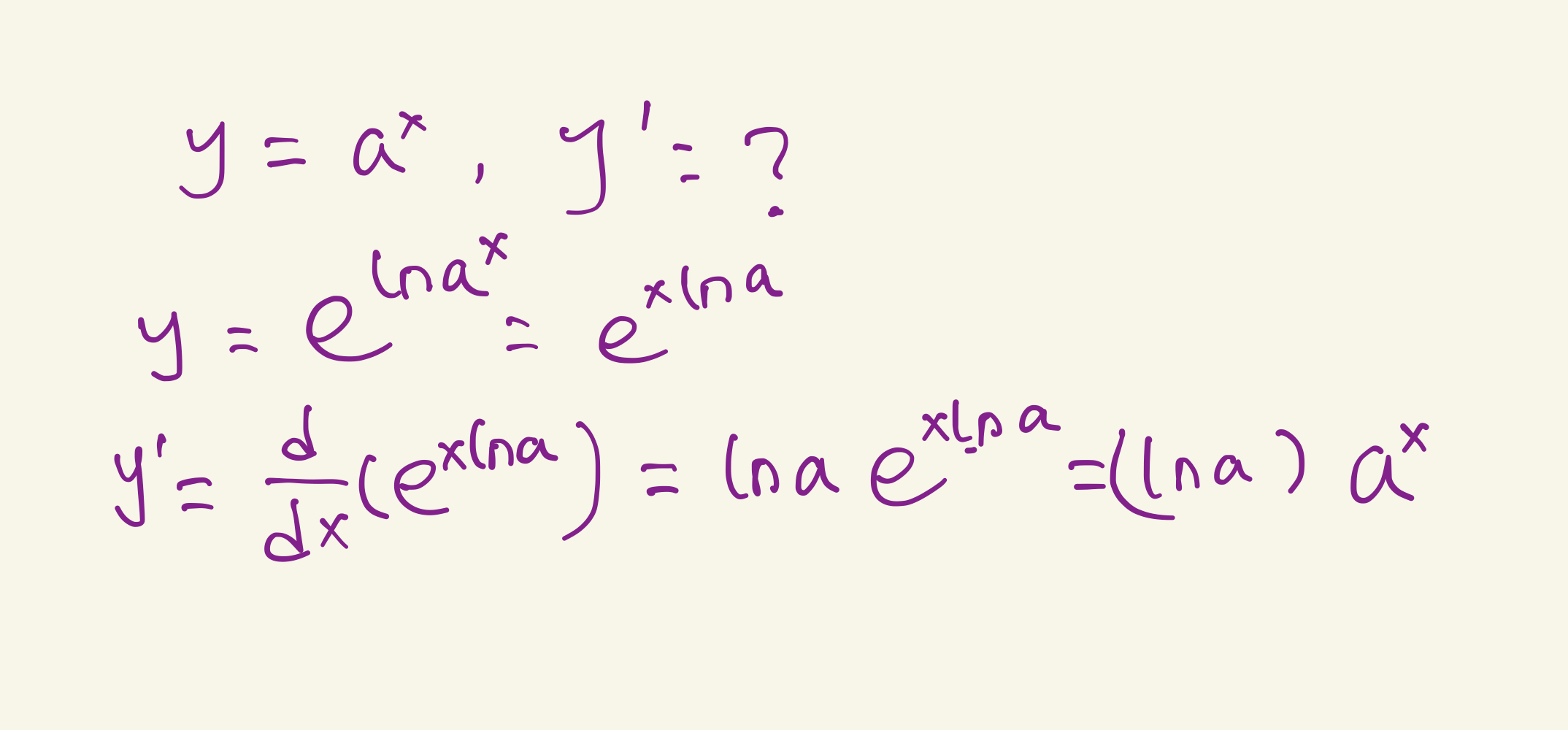
4. 对数微分法

接着看第二种，叫做对数微分法，所有的指数类型的函数我们都可以尝试用该种方法进行求导。先取原函数的对数，然后求导

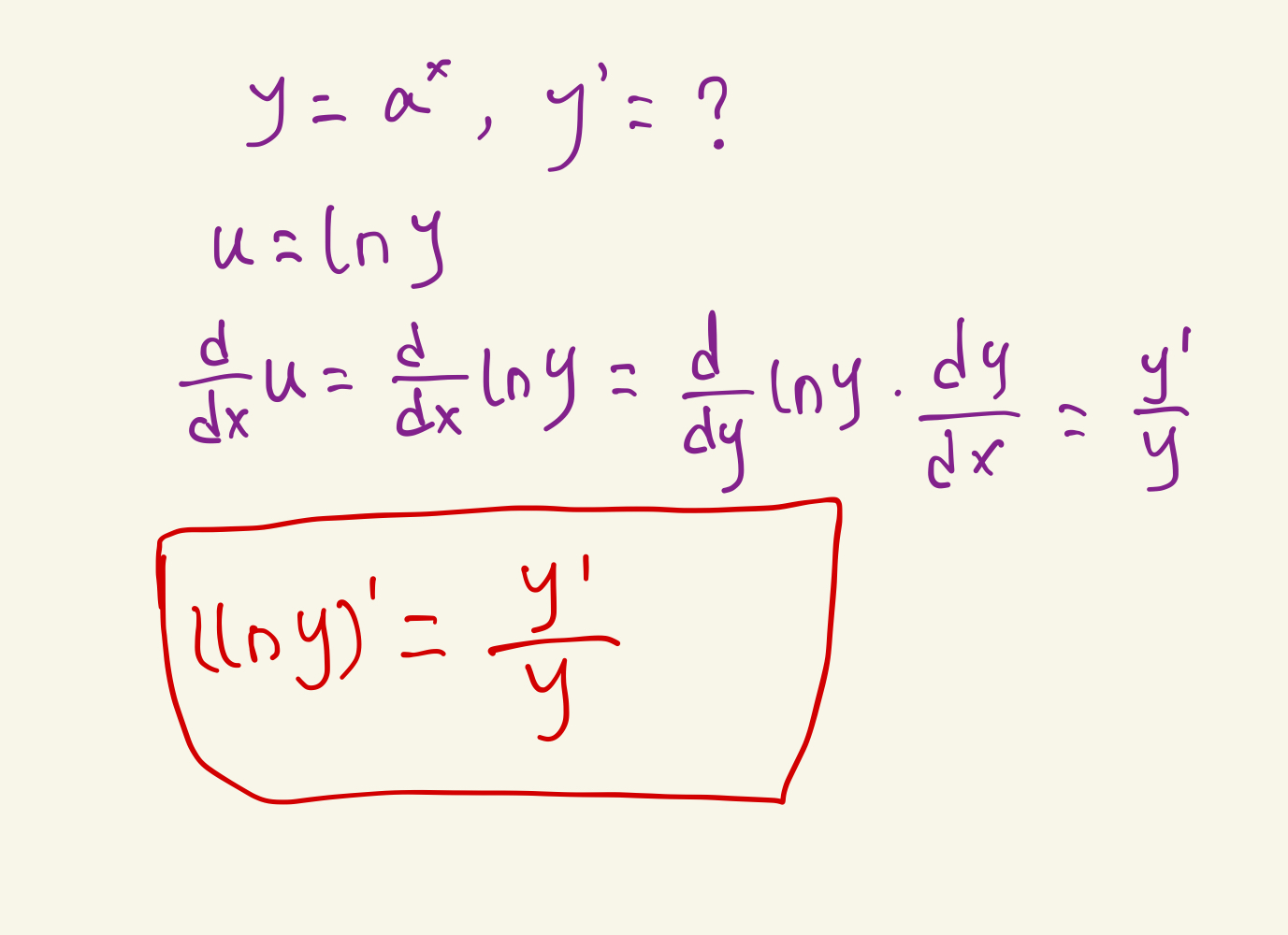
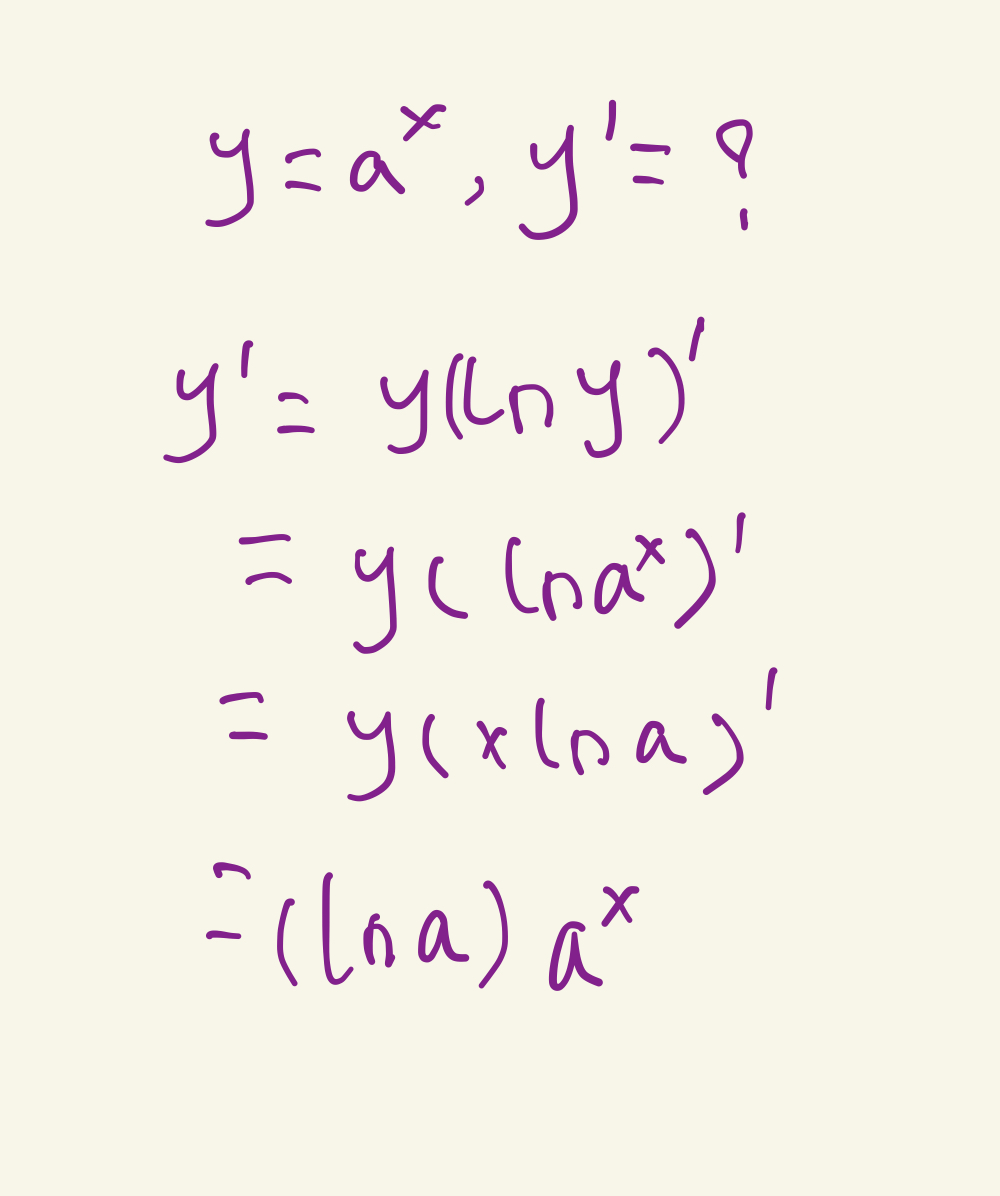
我们看到两种方式求出来的结果一致

再来看一个例子： \(y = x^x\)，我们两种方法都来一遍

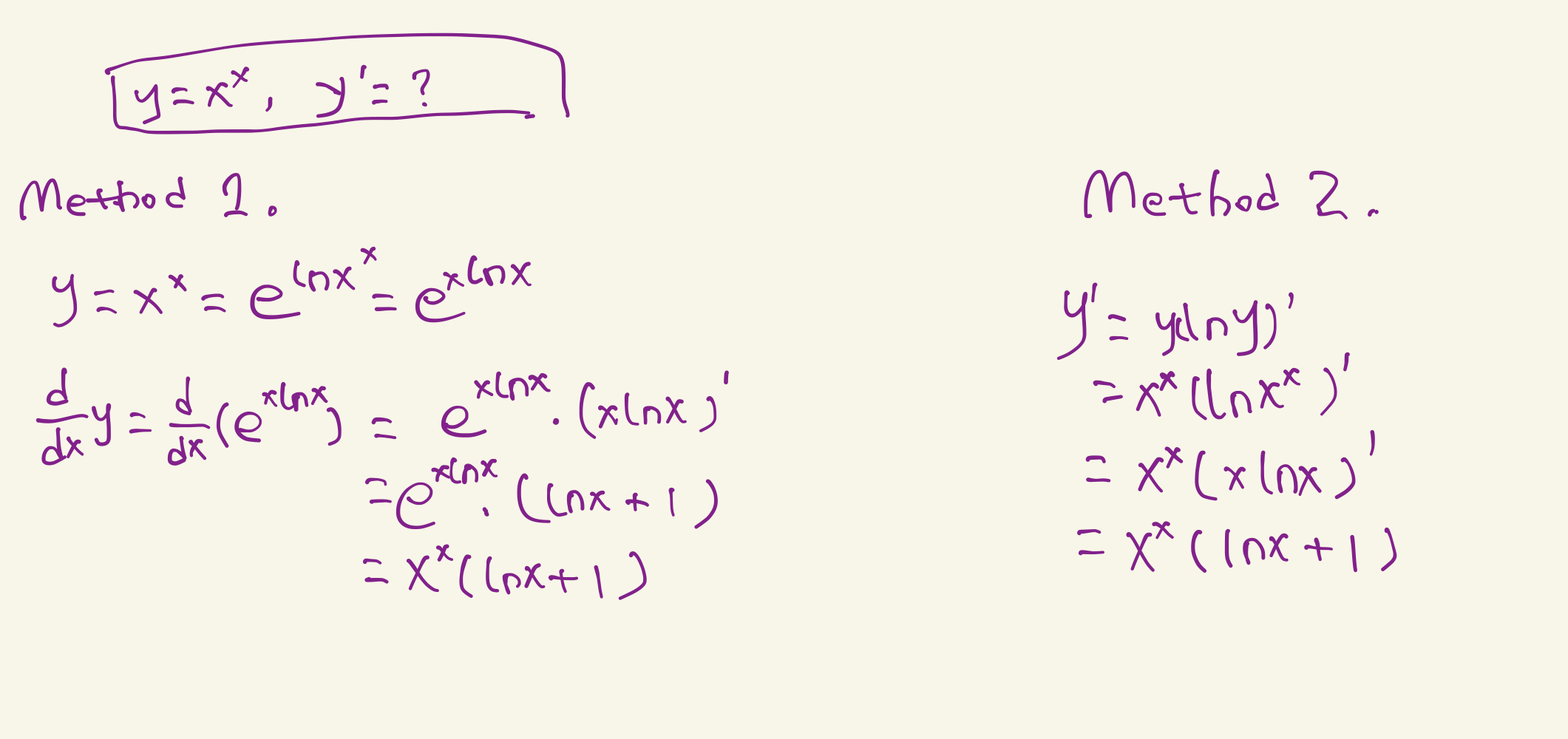
5. 总结

隐函数 —> 逆函数 —> 指数 —> 对数 这些函数的求导是层层递进的

有了隐函数求导的方式，我们在遇到一些较难直接求取原函数导数的情况下，可以选择求逆函数的导 \(f^{'} = \frac{1} {g^{'}}\)。有了逆函数求导，我们来到了指数相关的函数，对于这一类函数的求导，我们有两种方式，第一种是借助自然底数 \(e\) , 同时借助其一条特性 \(e^{ln x} = x\) 从而进行一些转换，转为求 \(e^y\) 这个函数的导

第二种就是对数微分法。我们求取其对数的导，然后再得到原函数的导 \(y^{'} = y\times(lny)^{'}\)

最后的最后，我们来看一个极限