保险精算--第12周作业

HW1

一笔贷款在 n > 5 年内等额分期偿还，每年末偿还一次，偿还金额为 X元，且已知
(1) 第 1 次还款额中的利息金额为 386.09 元；
(2) 第 3 次还款额中的利息金额为 323.16 元；
(3) 第 5 次还款额中的利息金额为 253.78 元；
计算 X

\[\begin{array}{l} x\left(1-y^{z}\right)-386.09=0 \\ x\left(1-y^{z-2}\right)-323.16=0 \\ x\left(1-y^{z-4}\right)-253.78=0 \end{array}\]

#wolframalpha
 Solve[{x*(1-y^z)-386.09=0 && x*(1-y^(z-2))-323.16=0 && x*(1-y^(z-4))-253.78=0}, {x, y, z}]

The Result Of HW1

HW2

投资者分别在 2017 年、2018 年和 2019 年的年初投资了 100 万元、150 万元和 300 万元。请根据下表数据计算该投资者在 2019 年可以分配到多少收益？

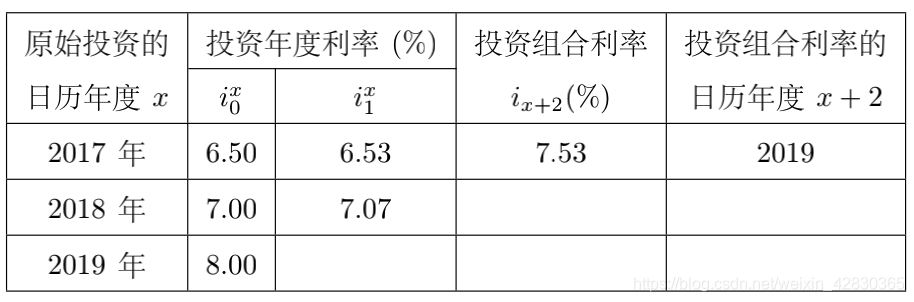
2019初:

\[100(1+0.065)(1+0.0653)+150(1+0.07)+300 \]

(Result1)
2019末：$$100(1+0.065)(1+0.0653)(1+0.0753)+150(1+0.07)(1+0.0707)+300(1+0.08)$$

(Result2)
末-初：$$\begin{array}{l}
(100(1+0.065)(1+0.0653)(1+0.0753)+150(1+0.07)(1+0.0707)+300(1+0.08))- \
(100(1+0.065)(1+0.0653)+150(1+0.07)+300)
\end{array}$$
The Result Of HW2

HW3

一笔 35 年期的贷款用等额分期偿还方法偿还，每年末偿还一次。第 8 次还款额中的利息金额为 937.5 元，第 22 次还款额中的利息金额为750 元。试求第 29 次还款额中的本金

\[\begin{array}{l} x\left(1-y^{28}\right)-937.5=0 \\ x\left(1-y^{14}\right)-750=0 \\ x\left(y^{7}\right)=z \end{array}\]

#wolframalpha
Solve[{x*(1-y^28)-937.5=0 && x*(1-y^14)-750=0 &&x*(y^7)=z }, {x,y,z}]

The Result Of HW3

HW4

一笔 10 年期的贷款用等额偿还方法偿还，每年末偿还一次。假设：
(1) 在最初的 3 年，偿还的本金之和为 2108.84 元；
(2) 在最后的 3 年，偿还的本金之和为 2775.09 元；
计算在整个偿还期内，支付的利息金额。

\[\begin{array}{l} x\left(1-y^{28}\right)-937.5=0 \\ x\left(1-y^{14}\right)-750=0 \\ z=x \times \frac{1-y^{10}}{\frac{1}{y}-1} \end{array}\]

The Result Of HW4

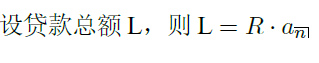
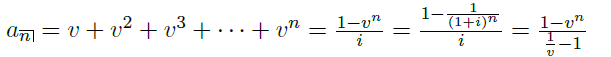
HW5

一笔 80 万元的 30 年期贷款，年实际利率为 6%，以等额分期方法偿还，每年末偿还一次。哪一年偿还的利息与本金最接近？

\[R\left(1-v^{30-t+1}\right)=R v^{30-t+1} \]

\[v^{30-t+1}=\frac{1}{2},v=\frac{1}{1+0.06} \]

\[\left(\frac{1}{1+0.06}\right)^{30-x+1}=\frac{1}{2} \]

The Result of HW5