Euler characteristic
Euler定理
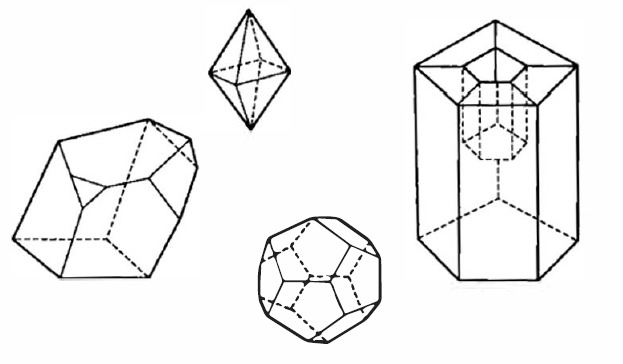
尽管我们有四个不同的四面体,但是如果我们将顶点数\((v)\)减去棱数\((e)\)再加上面的数目\((J)\)
引入:绝对值
distance\(:|a-b|\)
properties\(:(1)|x| \geq 0\),for all \(x \in R\),and \("=” \Leftrightarrow x=0\)
\((2):|a-b|=|b-a|(|x|=|-x|)\)
\((3):|x+y| \leq |x|+|y|\),for all \(x,y \in R\)
(\(|a-c| \leq |a-b|+|b-c|\))
度量空间
Distance function/metric space
Let \(X\) be a set.
\(\underline{Def:}\)A function \(X \times X \stackrel{d}{\longrightarrow}\mathbb{R}\)is called a distance function on \(X\)
1.\(\forall x,y\in X\),\(d(x,y)\geq 0\) and \("=” \Leftrightarrow x=y\)
2.\(\forall x,y\in X\),\(d(x,y)=d(y,x)\)
3.\(\forall x,y,z \in X\),\(d(x,z)\leq d(x,y)+d(y,z)\)
Example:
\(\mathfrak{A}:\)
1.\(x=(x_1,x_2,\dots,x_m),y=(y_1,y_2,\dots,y_m)\in \mathbb{R}^n\)
\(d_2(x,y):=\sqrt{|x_1-y_1|^2+\cdots+|x_m-y_m|^2}=|x-y|\)
\(d_2\) is a metric on \(\mathbb{R}^n\)(Cauchy inequality)
2.\(d_1(x,y):=|x_1-y_1|+|x_2-y_2|+\cdots+|x_m-y_m|\)
3.\(d_{\infty}(x,y)=max\{|x_1-y_1|,\dots,|x_m-y_m|\}\)
\(\mathfrak{B}:\)
X:a set.For \(x,y \in X\),let $$d(x,y):=\left{
\begin{aligned}
1&if&x\leq y
\
0&if&x =y
\end{aligned}
\right.
\[$d(x,y)\Rightarrow$the discrete metric
## 开集,闭集
we may generalize the definitions about limits and convergence to metric space
$\underline{Def}$ Let $(X,d)$ be a metric space,$a_n(n \in \mathbb{N})$be a seq in $\mathrm{X}$.and $\mathcal{L}$in X
$a_n(n \in \mathbb{N})$converges to $\mathcal{L}$
(1)For $r \geq 0$and $x_0 \in X$,we let $B_r(x_0)=\{x \in X|d(x,x_0)\leq r\}$(open ball)
(2).S is an open set(of$(X,d)$),if $\forall x \in S$,$\exists r >0$
($B_r(x_0)\subset S$)open ball $\Rightarrow$open set
EX:
$(X,d):$metric space.$x_0 \in X,r \geq 0$
Show that:(1)$B_r(x_0)$is open
(2)$\{x \in X|d(x,x_0)> r\}$is open
warning:A subset $S$ of a topological space $(X, \mathcal{T})$ is said to be clopen if it is both open and closed in $(X, \mathcal{T})$
Example. $\quad$ Let $X=\{a, b, c, d, e, f\}$ and
\]
\tau_{1}={X, \emptyset,{a},{c, d},{a, c, d},{b, c, d, e, f}}
\[We can see:
(i) the set $\{a\}$ is both open and closed;
(ii) the set $\{b, c\}$ is neither open nor closed;
(iii) the set $\{c, d\}$ is open but not closed;
(iv) the set $\{a, b, e, f\}$ is closed but not open.
In a discrete space every set is both open and closed, while in an indiscrete space$(X, \tau),$ all subsets of $X$ except $X$ and $\emptyset$ are neither open nor closed.
## Topological space
$\underline{Def:}$A topology space
$\mathcal{X}=(\underline{X},\eth_{x})$consists of a set $\underline{X}$,called the underlying space of $\mathcal{X}$ ,and a family $\eth_{x}$of subsets of $\mathcal{X}$(ie.$\eth_{x}\subset P(\underline{X})$)
$P(\underline{X})$means the power set of $\underline{X}$
s.t.:(1):$\underline{X}$ and $\varnothing \in \eth_{x}$
(2):$U_{\alpha}\in \eth_{x}(\alpha \in A) \Rightarrow$
$\cup_{\alpha \in A}U_{\alpha} \in \eth_{x}$
(3).$U,U^{\prime}\in \eth_{x} \Rightarrow U \cap U^{\prime} \in \eth_{x}$
$\eth_{x}$ is called a topology(topological structure) on $\underline{X}$
$\underline{Convention:}$We usually use $\mathcal{X}$ to indicate the set $\underline{X}$and omit the subscript $x$ in $\eth_{x}$ by saying "a topological space$(X,\eth)$"
$\underline{Examples:}$(1)metric space:
$(X,d) \looparrowright(X,\eth_{d})$(open sets induced by d)
$\bullet$Different distance funcs might determine the same topology
$\underline{Def:}$Let X and Y be topology spaces and $\underline{X}\stackrel{f}{\longrightarrow}\underline{Y}$a map.
We say that f is conti(from X to Y)
f is conti at a point $x_0 \in X$(from X to Y)
(1)if$\forall V \in f(x_0),V \in \eth_{Y},\exists x_0 \in U \in \eth_{x},f(U) \subset V$
(2)f is continuous(from X to Y)
if it is conti at every point of X
$\underline{Def:}$ X : top space
$K \subset \underline{X}$
K is compact on X if
$\forall U_{\alpha} \subset_{open} X$
## 什么是拓扑
我们从集合出发,在代数结构上我们得到群的性质
我们从拓扑结构上,我们能得到拓扑空间
## 拓扑空间
一个集合X上一个拓扑是X的子集的一个族$\Im$
它满足以下条件:
$(i) \varnothing$和$X$都要在$\Im$中
$(ii)\Im$的任意子族的元素的并都要在$\Im$中
$(iii)\Im$的任意有限子族的元素的交都要在$\Im$中
一个指定了拓扑$\Im$的集合X叫做一个拓扑空间(拓扑空间指的是有序对($\Im,X$),一般来说不专门提到$\Im$
从某种角度来说,我们可以认为拓扑空间指的是一个集合X连同它的子集的一个族(拓扑空间指的是集合的某种组合),拓扑本身来说就是集合为元素的集合,这里我们引入幂集的概念$2^{\mathcal{T}}$,$\mathcal{T} \subset 2^{\mathcal{T}}$
$X$的子集的全部组合我们称之为幂集$2^X$
### 例子:
==1.1:==$X=\{a,b,c,d,e,f\},\Im_{1} =\{X,\varnothing,\{a\},\{c,d\},\{a,c,d\},\{b,c,d,e,f\}\}$则$\Im_{1}$满足上述的性质,$\Im_{1}$为X上的一个拓扑
==1.2:==$X=\{a,b,c,d,e\},\Im_{2} =\{X,\varnothing,\{a\},\{c,d\},\{a,c,e\},\{b,c,d\}\}$,$\{a\}\cup\{c,d\} \nsubseteq \Im_{2}$,则$\Im_{2}$不是X上的拓扑
==1.3==$X=\{a,b,c,d,e\},\Im_{3} =\{X,\varnothing,\{a\},\{f\},\{a,c,f\},\{b,c,d,e,f\}\}$,$\{a\}\cap\{f\}\cap\{a,c,f\}\nsubseteq\Im_{3}$,则$\Im_{3}$不是X上的拓扑
==1.4==$\Im_{4}$为$\mathbb{N}$组成的所有有限子集,假设 $A_i={i} ,i$取遍所有大于1的整数。我们仔细想想,如果把所有的$A_{i}$并在一起,那就组成了$\mathbb{N}$,$\mathbb{N}$为无穷集合,与拓扑并的性质违背,$\Im_{4}$为$\mathbb{N}$组成的所有有限子集,$\Im_{4}$不是X上的拓扑
# Exercises
## HW1
**1.** 设 M 为正多面体,它的每个面有 p 个边,每个顶点是 q 个面的交点. 用Euler 定理$v − e + f = 2,$证明:
(a). $\frac{1}{p}+\frac{1}{q}=\frac{1}{2}+\frac{1}{e}$
(b). 由 (a) 证明正多面体只有 5 种.
**2.** 计算由立方体按下图中箭头粘合边并且对面两两粘合(即上表面和底面粘合,前表面和后表面粘合,左侧面和右侧面粘合)得到的商空间的Euler示性数
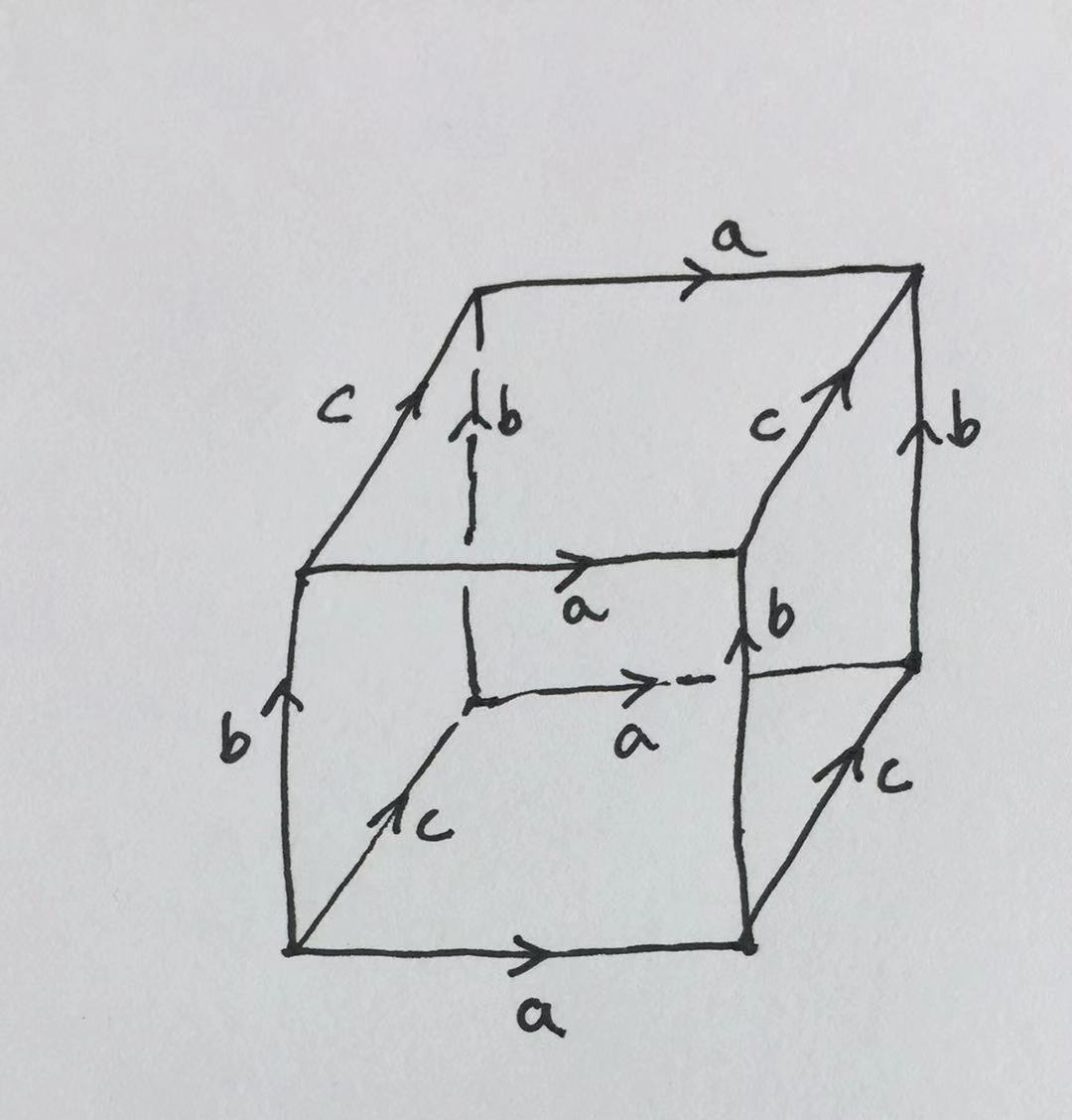
## HW3
**1.** 设 $\mathcal{T}$ 是 $X$ 上的拓扑,A 是 $X$ 的一个子集,规定:
$\mathcal{T}^{\prime}=\{A \cup U \quad | U \in \mathcal{T}\} \cup\{\emptyset\}$
证明:$\mathcal{T}^{\prime}$也是$X$上的拓扑
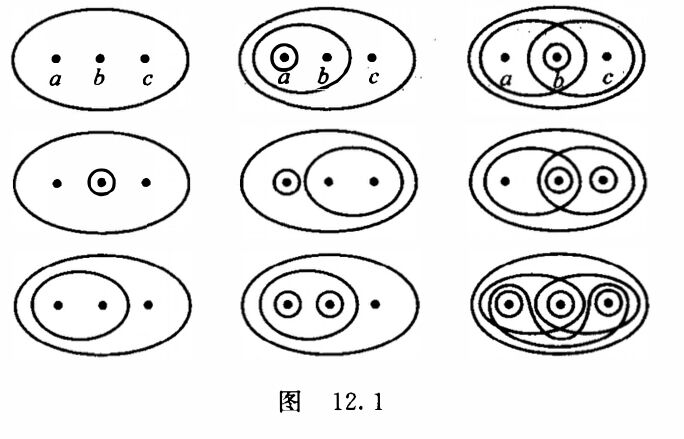
**2.** 设集合$X = \{a,b,c\}$, 请给出 $X$上的所有可能的拓扑.
## HW4
**3.** 设$X$是一个拓扑空间,则对于任意 $A,B\subset X$ 有:
(a). $(A \cap B)^{\circ}=A^{\circ} \cap B^{\circ}$
(b). $A^{\circ \circ}=A^{\circ}$
**4.** 证明:每一个离散拓扑空间都是可度量化的。( 提示:注意到离散拓扑空间的任意子集都是开集,要证明其可度量化,只需说明存在⼀个度量,使得空间的任意⼀个子集都可以表示成⼀些由该度量定义的开球的并.)
## HW5
**3.** 度量空间的每个子集的导集是闭集.\]


