数据预处理:独热编码(One-Hot Encoding)和 LabelEncoder标签编码
一、问题由来
在很多机器学习任务中,特征并不总是连续值,而有可能是分类值。
离散特征的编码分为两种情况:
1、离散特征的取值之间没有大小的意义,比如color:[red,blue],那么就使用one-hot编码
2、离散特征的取值有大小的意义,比如size:[X,XL,XXL],那么就使用数值的映射{X:1,XL:2,XXL:3}
使用pandas可以很方便的对离散型特征进行one-hot编码
import pandas as pd df = pd.DataFrame([ ['green', 'M', 10.1, 'class1'], ['red', 'L', 13.5, 'class2'], ['blue', 'XL', 15.3, 'class1']]) df.columns = ['color', 'size', 'prize', 'class label'] size_mapping = { 'XL': 3, 'L': 2, 'M': 1} df['size'] = df['size'].map(size_mapping) class_mapping = {label:idx for idx,label in enumerate(set(df['class label']))} df['class label'] = df['class label'].map(class_mapping)
例如,考虑一下的三个特征:
["male", "female"] ["from Europe", "from US", "from Asia"] ["uses Firefox", "uses Chrome", "uses Safari", "uses Internet Explorer"]
如果将上述特征用数字表示,效率会高很多。例如:
["male", "from US", "uses Internet Explorer"] 表示为[0, 1, 3] ["female", "from Asia", "uses Chrome"]表示为[1, 2, 1]
但是,即使转化为数字表示后,上述数据也不能直接用在我们的分类器中。因为,分类器往往默认数据数据是连续的(可以计算距离?),并且是有序的(而上面这个0并不是说比1要高级)。但是,按照我们上述的表示,数字并不是有序的,而是随机分配的。
独热编码
为了解决上述问题,其中一种可能的解决方法是采用独热编码(One-Hot Encoding)。独热编码即 One-Hot 编码,又称一位有效编码,其方法是使用N位状态寄存器来对N个状态进行编码,每个状态都由他独立的寄存器位,并且在任意时候,其中只有一位有效。
例如:
自然状态码为:000,001,010,011,100,101 独热编码为:000001,000010,000100,001000,010000,100000
可以这样理解,对于每一个特征,如果它有m个可能值,那么经过独热编码后,就变成了m个二元特征(如成绩这个特征有好,中,差变成one-hot就是100, 010, 001)。并且,这些特征互斥,每次只有一个激活。因此,数据会变成稀疏的。
这样做的好处主要有:
-
解决了分类器不好处理属性数据的问题
-
在一定程度上也起到了扩充特征的作用
实现方法一:pandas之get_dummies方法
pandas.get_dummies(data, prefix=None, prefix_sep='_', dummy_na=False, columns=None, sparse=False, drop_first=False)
该方法可以讲类别变量转换成新增的虚拟变量/指示变量。
常用参数
data : array-like, Series, or DataFrame 输入的数据 prefix : string, list of strings, or dict of strings, default None get_dummies转换后,列名的前缀 *columns : list-like, default None 指定需要实现类别转换的列名 dummy_na : bool, default False 增加一列表示空缺值,如果False就忽略空缺值 drop_first : bool, default False 获得k中的k-1个类别值,去除第一个
1、实验

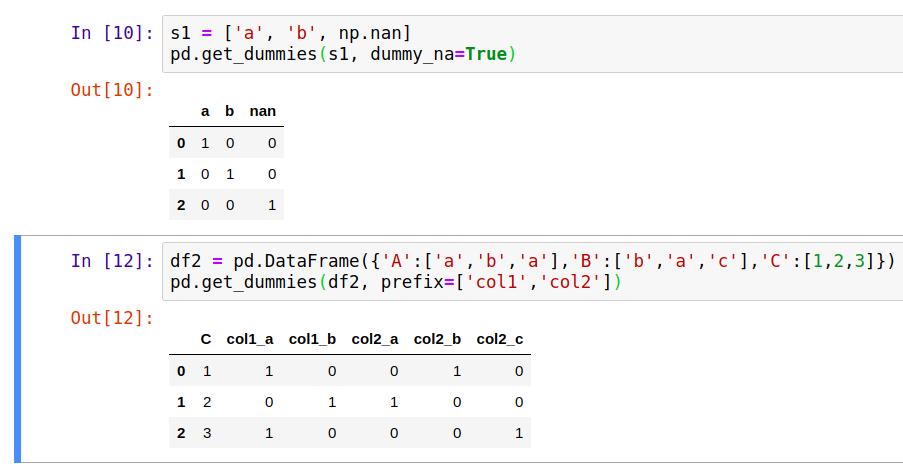
实现方法二:sklearn
from sklearn import preprocessing enc = preprocessing.OneHotEncoder() enc.fit([[0, 0, 3], [1, 1, 0], [0, 2, 1], [1, 0, 2]]) # fit来学习编码 enc.transform([[0, 1, 3]]).toarray() # 进行编码
输出:array([[ 1., 0., 0., 1., 0., 0., 0., 0., 1.]])
数据矩阵是4*3,即4个数据,3个特征维度。
0 0 3 观察左边的数据矩阵,第一列为第一个特征维度,有两种取值0\1. 所以对应编码方式为10 、01
1 1 0 同理,第二列为第二个特征维度,有三种取值0\1\2,所以对应编码方式为100、010、001
0 2 1 同理,第三列为第三个特征维度,有四中取值0\1\2\3,所以对应编码方式为1000、0100、0010、0001
1 0 2
再来看要进行编码的参数[0 , 1, 3], 0作为第一个特征编码为10, 1作为第二个特征编码为010, 3作为第三个特征编码为0001. 故此编码结果为 1 0 0 1 0 0 0 0 1
三. 为什么要独热编码?
正如上文所言,独热编码(哑变量 dummy variable)是因为大部分算法是基于向量空间中的度量来进行计算的,为了使非偏序关系的变量取值不具有偏序性,并且到圆点是等距的。使用one-hot编码,将离散特征的取值扩展到了欧式空间,离散特征的某个取值就对应欧式空间的某个点。将离散型特征使用one-hot编码,会让特征之间的距离计算更加合理。离散特征进行one-hot编码后,编码后的特征,其实每一维度的特征都可以看做是连续的特征。就可以跟对连续型特征的归一化方法一样,对每一维特征进行归一化。比如归一化到[-1,1]或归一化到均值为0,方差为1。
为什么特征向量要映射到欧式空间?
将离散特征通过one-hot编码映射到欧式空间,是因为,在回归,分类,聚类等机器学习算法中,特征之间距离的计算或相似度的计算是非常重要的,而我们常用的距离或相似度的计算都是在欧式空间的相似度计算,计算余弦相似性,基于的就是欧式空间。
四 .独热编码优缺点
- 优点:独热编码解决了分类器不好处理属性数据的问题,在一定程度上也起到了扩充特征的作用。它的值只有0和1,不同的类型存储在垂直的空间。
- 缺点:当类别的数量很多时,特征空间会变得非常大。在这种情况下,一般可以用PCA来减少维度。而且one hot encoding+PCA这种组合在实际中也非常有用。
五. 什么情况下(不)用独热编码?
- 用:独热编码用来解决类别型数据的离散值问题,
- 不用:将离散型特征进行one-hot编码的作用,是为了让距离计算更合理,但如果特征是离散的,并且不用one-hot编码就可以很合理的计算出距离,那么就没必要进行one-hot编码。 有些基于树的算法在处理变量时,并不是基于向量空间度量,数值只是个类别符号,即没有偏序关系,所以不用进行独热编码。 Tree Model不太需要one-hot编码: 对于决策树来说,one-hot的本质是增加树的深度。
总的来说,要是one hot encoding的类别数目不太多,建议优先考虑。
六. 什么情况下(不)需要归一化?
- 需要: 基于参数的模型或基于距离的模型,都是要进行特征的归一化。
- 不需要:基于树的方法是不需要进行特征的归一化,例如随机森林,bagging 和 boosting等。
七、one-hot编码为什么可以解决类别型数据的离散值问题
首先,one-hot编码是N位状态寄存器为N个状态进行编码的方式
eg:高、中、低不可分,→ 用0 0 0 三位编码之后变得可分了,并且成为互相独立的事件
类似 SVM中,原本线性不可分的特征,经过project之后到高维之后变得可分了
GBDT处理高维稀疏矩阵的时候效果并不好,即使是低维的稀疏矩阵也未必比SVM好
八、Tree Model不太需要one-hot编码
对于决策树来说,one-hot的本质是增加树的深度
tree-model是在动态的过程中生成类似 One-Hot + Feature Crossing 的机制
1. 一个特征或者多个特征最终转换成一个叶子节点作为编码 ,one-hot可以理解成三个独立事件
2. 决策树是没有特征大小的概念的,只有特征处于他分布的哪一部分的概念
one-hot可以解决线性可分问题 但是比不上label econding
one-hot降维后的缺点:
- 降维前可以交叉的降维后可能变得不能交叉


 浙公网安备 33010602011771号
浙公网安备 33010602011771号