梯度下降法的三种形式-BGD、SGD、MBGD
在应用机器学习算法时,我们通常采用梯度下降法来对采用的算法进行训练。其实,常用的梯度下降法还具体包含有三种不同的形式,它们也各自有着不同的优缺点。
下面我们以线性回归算法来对三种梯度下降法进行比较。
一般线性回归函数的假设函数为:
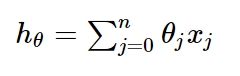
对应的损失函数为:
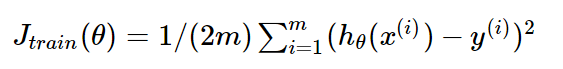
下图为一个二维参数(θ0和θ1)组对应能量函数的可视化图:
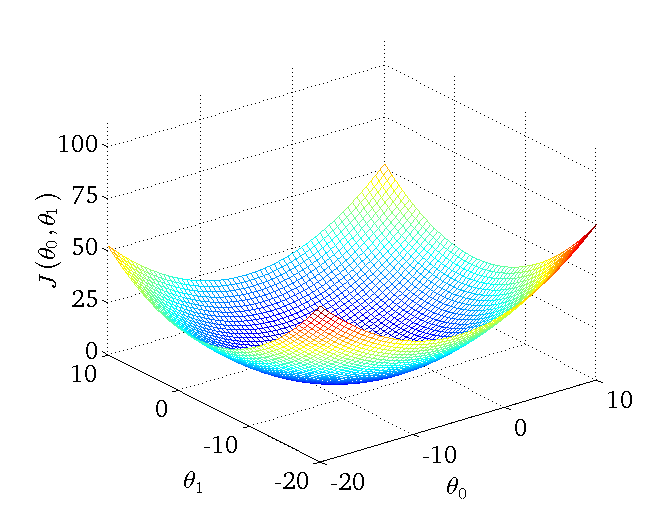
1、批量梯度下降法BGD
批量梯度下降法(Batch Gradient Descent,简称BGD)是梯度下降法最原始的形式,它的具体思路是在更新每一参数时都使用所有的样本来进行更新。
我们的目的是要误差函数尽可能的小,即求解weights使误差函数尽可能小。首先,我们随机初始化weigths,然后不断反复的更新weights使得误差函数减小,直到满足要求时停止。这里更新算法我们选择梯度下降算法,利用初始化的weights并且反复更新weights:
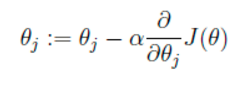
这里代表学习率,表示每次向着J最陡峭的方向迈步的大小。为了更新weights,我们需要求出函数J的偏导数。首先当我们只有一个数据点(x,y)的时候,J的偏导数是:

则对所有数据点,上述损失函数的偏导(累和)为:

再最小化损失函数的过程中,需要不断反复的更新weights使得误差函数减小,更新过程如下:
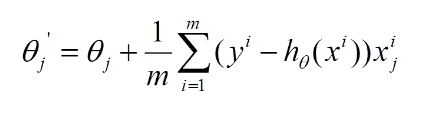
那么好了,每次参数更新的伪代码如下:
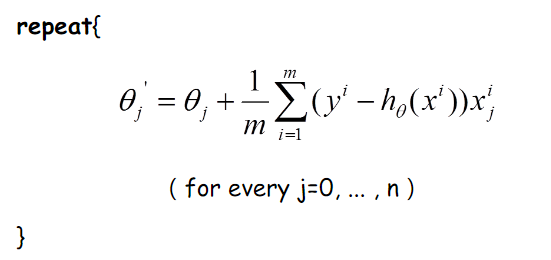
由上图更新公式我们就可以看到,我们每一次的参数更新都用到了所有的训练数据(比如有m个,就用到了m个),如果训练数据非常多的话,是非常耗时的。
下面给出批梯度下降的收敛图:
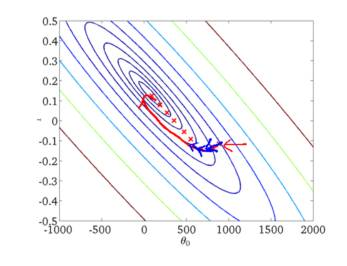
从图中,我们可以得到BGD迭代的次数相对较少。
代码实现:
def batchGradientDescent(x, y, theta, alpha, m, maxIteration): for i in range(maxIteration): hypothesis = np.dot(x, theta) loss = hypothesis - y gradient = np.dot(x.transpose(), loss) / m theta = theta - alpha * gradient # 对所有样本求和 return theta
2、随机梯度下降法SGD
由于批梯度下降每跟新一个参数的时候,要用到所有的样本数,所以训练速度会随着样本数量的增加而变得非常缓慢。随机梯度下降正是为了解决这个办法而提出的。它是利用每个样本的损失函数对θ求偏导得到对应的梯度,来更新θ:
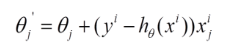
更新过程如下:

随机梯度下降是通过每个样本来迭代更新一次,对比上面的批量梯度下降,迭代一次需要用到所有训练样本(往往如今真实问题训练数据都是非常巨大),一次迭代不可能最优,如果迭代10次的话就需要遍历训练样本10次。
但是,SGD伴随的一个问题是噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向。
随机梯度下降收敛图如下:
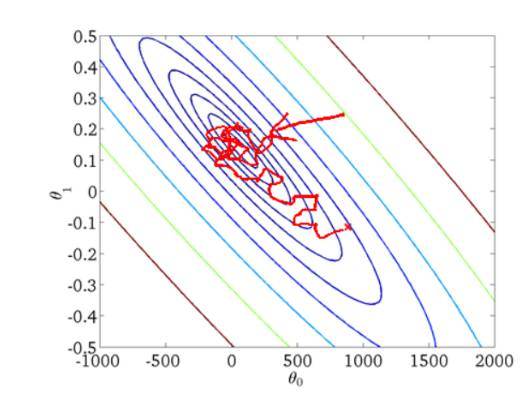
我们可以从图中看出SGD迭代的次数较多,在解空间的搜索过程看起来很盲目。但是大体上是往着最优值方向移动。
代码实现:
def StochasticGradientDescent(x, y, theta, alpha, m, maxIteration): data = [] for i in range(10): data.append(i) # 这里随便挑选一个进行更新点进行即可(不用想BGD一样全部考虑) for i in range(maxIteration): hypothesis = np.dot(x, theta) loss = hypothesis - y # 这里还是有十个样本 index = random.sample(data, 1)[0] # 随机抽取一个样本,得到它的下标 gradient = loss[index] * x[index] # 只取一个点进行更新计算 theta = theta - alpha * gradient.T return theta
3、min-batch 小批量梯度下降法MBGD
我们从上面两种梯度下降法可以看出,其各自均有优缺点,那么能不能在两种方法的性能之间取得一个折衷呢?既算法的训练过程比较快,而且也要保证最终参数训练的准确率,而这正是小批量梯度下降法(Mini-batch Gradient Descent,简称MBGD)的初衷。
我们假设每次更新参数的时候用到的样本数为10个(不同的任务完全不同,这里举一个例子而已)
更新伪代码如下:
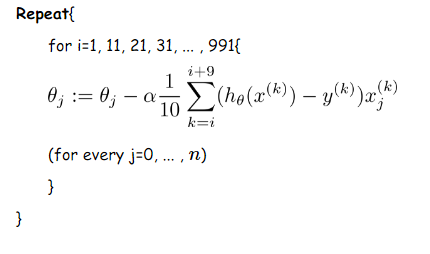
4、三种梯度下降方法的总结
1.批梯度下降每次更新使用了所有的训练数据,最小化损失函数,如果只有一个极小值,那么批梯度下降是考虑了训练集所有数据,是朝着最小值迭代运动的,但是缺点是如果样本值很大的话,更新速度会很慢。
2.随机梯度下降在每次更新的时候,只考虑了一个样本点,这样会大大加快训练数据,也恰好是批梯度下降的缺点,但是有可能由于训练数据的噪声点较多,那么每一次利用噪声点进行更新的过程中,就不一定是朝着极小值方向更新,但是由于更新多轮,整体方向还是大致朝着极小值方向更新,又提高了速度。
3.小批量梯度下降法是为了解决批梯度下降法的训练速度慢,以及随机梯度下降法的准确性综合而来,但是这里注意,不同问题的batch是不一样的。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号